Разложение сложного риска на простые путем построения дерева решений по конкретной хозяйственной ситуации, с которой сталкивается фирма. Идентификация рисков хозяйственных субъектов, страница 2

Если SFr 2,3 за 1 ф.ст.

Валюта	Покупка	Продажа	Прибыль британской компании
$		2 млн.
SFr	1 млн.
Ф. ст.	0,65 млн.	1 млн.	0,35 млн.

Из расчётов видно, что британская компания может получить прибыль в 0,4 млн. ф.ст.

Если курс станет $2,2 за 1 ф.ст., прибыль британской компании уменьшится до 0,3 млн. ф.ст.

Если же SFr 2,3 за 1 ф.ст. британская компания получит прибыль 0,35 млн. ф.ст.

РАЗДЕЛ 4

Задание 1

 Пекарня печет хлеб на продажу магазинам. Стоимость одной булки составляет 30 пенсов, ее продают за 40 пенсов. В таблице приведены данные о спросе за последние 50 дней:

Спрос, тыс. шт / день	10	12	14	16	18
Число дней	5	10	15	15	5

Если булка испечена, на не продана, то убытки составляют 20 пенсов за штуку. Определите, сколько булок нужно выпекать в день.

1. По критерию Вальда

Критерий А. Вальда исходит из задачи полного исключения риска. Для этого из всех возможных при разных стратегиях показателей прибыли отбираются самые низкие. Далее уже из них выбирается самый высокий.

Такую модель принятия решений принимают исходя из того, что условия хозяйственной деятельности, скорее всего, будут неблагоприятными.

Для нахождения самого высокого показателя прибыли строим матрицу, где условиями выступают различные показатели числа булок, которые, возможно, следует выпекать и величина спроса на аналогичное количество продукции.

Таблица 1.1

Предложение для продажи, тыс. шт/день	Спрос, тыс.шт/день
	10	12	14	16	18
10	100	100	100	100	100
12	40	120	120	120	120
14	-20	60	140	140	140
16	-80	0	80	160	160
18	-140	-60	20	100	120

Отбираем самые низкие показатели прибыли и заносим в таблицу, для выявления самого высокого из них:

Таблица 1.2

Предложение для продажи, тыс. шт/день	Самые низкие показатели прибыли
10	100
12	40
14	-20
16	-80
18	-140

Таким образом, оптимальная стратегия, в соответствии с этим правилом, - это выпекать 10 тыс. булок в день, что обеспечит относительно высокую прибыль при самых неблагоприятных условиях.

2. По критерию Лапласа

Принимается, что наступление каждой ситуации одинаково вероятно: поэтому избирают стратегию со средними прибылью, наивысшей во всех ситуациях. Вычислим среднюю величину прибыли для каждого предложения перкарни и выберем самую высокую среднюю величину прибыли:

Для предложения 10 тыс. булок: (100+100+100+100+100)/5=100 (тыс. пенсов)

Для предложения 12 тыс. булок: (40+120+120+120+120)/5=104 (тыс. пенсов)

Для предложения 14 тыс. булок: (-20+60+140+140+140)/5=92 (тыс. пенсов)

Для предложения 16 тыс. булок: (-80+80+0+160+160)/5=64 (тыс. пенсов)

Для предложения 18 тыс. булок: (-140-60+20+100+180)/5=20 (тыс. пенсов).

Как видно из расчетов в нашем случае средняя величина прибыли выше при предложении пекарни выпекать 12 тыс. булок в день, т.к. средняя величина прибыли составит 104 тыс. пенсов.

Задание 1

Фирма рассматривает два инвестиционных проекта производства консервированных овощей. Схемы инвестирования и получения дохода отражены в таблице. Экспертно оценена вероятность достижения прогнозируемых результатов (дохода).

Предполагаемая ставка процента за рассматриваемый период  – 10 %. Какой из проектов выберет фирма, максимизирующая прибыль?

Инвестиции	2003 г	2004 г	2005 г	Всего
1-й проект	100	60	-	160
2-й проект	40	40	80	160
Доход
1-й проект	-	-	2200	2200
2-й проект	-	1000	1200	2200
Вероятность
1-й проект	1	1	0,85
2-й проект	1	0,9	0,81

Средний ожидаемый доход проекта 1 составляет

                        2200*0.85=1870;

            для проекта 2 соответственно

                        1000*0.9+1200*0.81=1872.

Для принятия окончательного решения необходимо определить сегодняшнюю ценность будущих поступлений и чистую приведенную стоимость с учетом вероятности получения доходов для двух инвестиционных проектов.

	2003 г.	2004 г.	2005 г.	Итого
Дисконтирующий множитель (1+r)n	1+0,1	1,2	1,3
Сегодняшняя ценность будущих поступлений	0	0	2200/1,3=1692	1692
	0	1000/1,2=833	1200/1,3=923	1756
Инвестиции	100/1,1=90	60/1,2=50	0	140
	40/1,1=36	40/1,2=33	80/1,3=62	131

Рассчитаем чистую приведенную стоимость инвестиционных проектов с учетом риска, принимая во внимание вероятность получения будущих денежных поступлений.

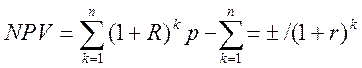
Для проекта 1:

            NPV=1692*0.85-40=1298.2

Для проекта 2:

            NPV=833*0.9+923-0.81-131=750+748-131=1367

Задание 3

Фирма сдает автомобили в аренду. За аренду автомобиля в год она получает 2000 ден. ед. Необходимо принять решение относительно целесообразности покупки еще одного автомобиля такого же класса, если его цена 8000 ден. ед. Через четыре года остаточная стоимость его составит 4000 ден. ед. , % = 10, а темп инфляции 4% ежегодно. С каким риском сталкивается фирма и какой метод количественной оценки риска используется?

Фирма сталкивается с инвестиционным риском. Инвестиционный риск состоит в вероятности потери вкладываемого капитала (в реальные активы или в финансовые) или ожидаемого дохода. В основе анализа инвестиционного риска лежит оценка и сравнение объема предполагаемых инвестиций и будущих денежных поступлений.

Используется метод дисконтирования, который позволяет определить ценность будущих поступлений:

,

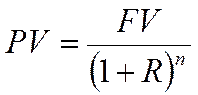где      PV – сегодняшняя ценность будущих поступлений;

            FV – будущие поступления;

            R   – процент;

            n   – количество лет.

Исходя из условия задачи, общая накопленная величина дисконтированных доходов за четыре года будет равна:

,

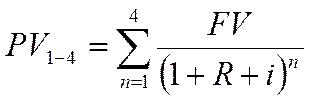где      і – темп инфляции.

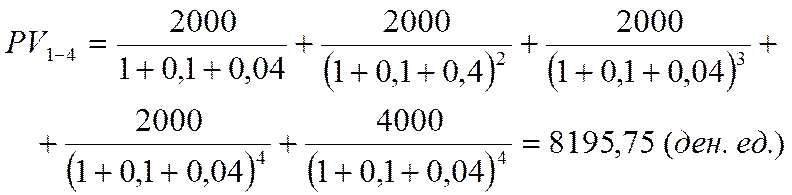
Чистый приведенный эффект проекта рассчитывается по формуле:

,

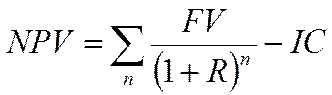где      IC – первоначальная инвестиция.

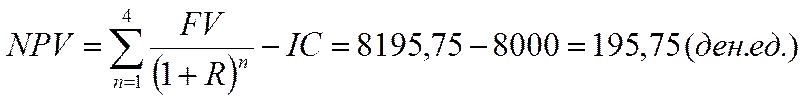
Учитывая то, что NPV>0, то для фирмы будет целесообразно купить еще один автомобиль.