Методические рекомендации к практическим работам № 1-9 по математике (Дифференцирование сложной функции. Графический метод решения задач линейного программирования)

Определить скорость J изменения функции в любой момент времени t (J - в амперах, t - в секундах). (Ответ: J=2cos(2t+1)k

Практическая работа № 4

Тема. Интегрирование функций.

Время 2 часа.

Методические рекомендации.

Необходимо повторить основные свойства неопределенного интеграла и таблицу интегралов. Необходимо помнить, что перед применением формулы интегрирования иногда  требуется преобразовать подынтегральное выражение.

Например, 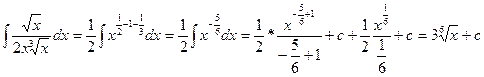, т.е. подынтегральное выражение приведено к виду хⁿ, применена формула

Найти интегралы:

1.                                               6.

2.                                                 7.  

3.                               8.

4.                                         9.

5.

Примеры интегрирования подстановкой (замены переменной).

Помните, что заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения. (не считая постоянного множителя.

1.          2.            3.            4.

5.                       6.                 7.

8.                            9.                          10.

Практическая №5

Тема. Вычисление площадей с помощью определенного интеграла.

Время 2 часа.

Методические рекомендации.

Перед выполнением работы необходимо повторить геометрический смысл определенного интеграла, графики  основных элементарных функций, способы вычисления площадей плоских фигур в зависимости от их расположения на координатной плоскости.

Задача 1. Вычислить площадь криволинейной трапеции, ограниченной осью ох, прямыми х=-1, х=2 и параболой у=9-х² (Ответ: 24

Задача 2. Найти площадь фигуры, ограниченной отрезком [0;] оси ох и графиком функции у=сosx на этом отрезке. (Ответ: 1(кв.ед.))

Задача 3. Вычислить площади фигур, ограниченных заданными линиями:

а) х-2у+4, 3х+2у-12=0 и у=0   Ответ: 12 кв.ед.

б) у=²=х и у=х²   Ответ (1/3 кв.ед.)

в) х-у-1=0, х=-4, х=-2 и у=0

г) у=х²-6х и х=0

д) у=cosx, х=3П/2 и осями ох и оу

Практическая работа №6

Тема. Вычисление определенного интеграла методом подстановки.

Время 2 часа.

Методические рекомендации.

По курсу лекций необходимо повторить вычисление определенных интегралов способом замены переменной. Помните, что нет необходимости возвращаться к первоначальной переменной, но, заменяя переменную под знаком интеграла, следует изменить и пределы интегрирования.

Вычислите интегралы.

1.                                               Ответ: 68

2.                                             Ответ: 48.4

3. 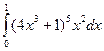                                          Ответ: 217

4. 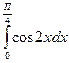                                                    Ответ: 1/2

5. 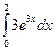                                                       Ответ: е⁶-1

6. 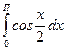                                                     Ответ: 2

7. 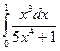                                                      Ответ: 1/20 In6

8.                                                      Ответ: 1

9. 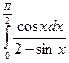                                                     Ответ:In2

10.    

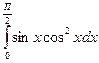
Практическая работа № 7

Тема. Применение определенного интеграла к решению физических задач.

Время 2 часа.

Методические рекомендации.

Необходимо повторить:

- нахождение пути, пройденного телом при прямолинейном движении;

- вычисление объема тела вращения;

- вычисление или сжатие пружины.

Задача 1. Скорость движения материальной точки задается формулой V=(4t³-2t+1) м/с. Найти путь, пройденный точкой за первые 4с от начала движения. (Ответ: 244 м)

Задача 2. Найти путь, пройденный телом за 10-ю секунду, зная, что скорость его прямолинейного движения выражается формулой V=(t²+4t-2) м/с. (Ответ: 126.3 м)

Задача 3. Тело брошено вертикально вверх со скоростью, которая изменяется по закону V=(29/4-9/8) м/с

Задача 4. Сила в 60 Н растягивает пружину на 2 см. Первоначальная длина пружины равна 14 см. Какую работу нужно совершить, чтобы растянуть ее до 20 см? (Ответ: 5.4 Дж)

Задача 5. При растяжении пружины на 5 см  затрачивается работа 29.43 Дж. На сколько растянется пружина, если затратить работу 9.81 Дж? (Ответ: 0.029м)

Задача 6. Найти объем тела, полученного при вращении вокруг оси ох криволинейной трапеции, ограниченной линиями : у=1-х² и у=0.   (Ответ: 1 куб. ед.)

Задача 7. Найти объем тела, полученного вращением вокруг оси оу трапеции, образованной линиями: у=3х, у=2, у=4, х=0  (Ответ: 56/27 П куб.ед.)

Практическая работа №8

Тема. Решение систем уравнений по формулам Крамера и методом Гаусса.

Время 2 часа.

Методические рекомендации.

Необходимо повторить:

- вычисление определителей второго и третьего порядка.

- свойства определителя.

- формулы Крамера.

-. Элементарные преобразования уравнений системы.

Решить системы по формулам Крамера.

1.            2.              3.

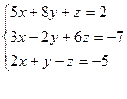
Ответ: (-3;2;1)

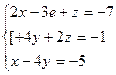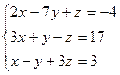4.      5.        6.

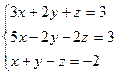
Ответ: (1;-1;2)

Решить системы методом Гаусса.

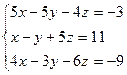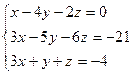1.       2.      3.

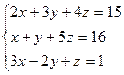
Ответ: (0;-1;2)              Ответ: (-2;-3;5)            Ответ: (0;1;3)

4. 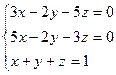                     5.                               

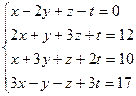
Ответ: (1/4;1;-1/4)                       Ответ: (1;-1;2;5)

Практическая работа №9

Тема. Графический метод решения задач линейного программирования.

Время 2 часа.

Методические рекомендации.

Повторить принцип  построения математической модели задач линейного программирования, а также способы решения систем линейных уравнений и неравенств.

Решите задачи.

1. Пусть система ограниченной задана уравнениями

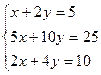
А линейная функция имеет вид f=х+у. Найти оптимальное решение, при котором функция f имеет максимальное значение. (Ответ: f_max=5 при х=5 и у=0)

2. Пусть задача линейного программирования  сводится к системе неравенств.

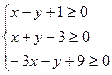, где х  у, а f=x-y+1

Найти значение переменных х и у, при которых функция f принимает минимальное значение.

(Ответ: f_min=0)

3. Пусть на некотором предприятии, выпускающем изделия двух типов, производственная мощность - 100 изделий первого типа или 300 изделий второго. ОТК в состоянии проверить не более 150 изделий любого типа. Найти такой план выпуска продукции, который обеспечивал бы предприятию наибольшую прибыль.

4. Швейная мастерская изготовляет женские костюмы и платья из тканей одного вида 1.5 м, а второго - 0.5 м., на костюм - соответственно 1.6 м. и 0.8 м. Доход мастерской от реализации одного костюма составляет 50 руб, а от реализации одного платья - 30 руб. Установите, сколько платье и костюмов необходимо сшить в мастерской