Графики распределения, дисперсия и математическое ожидание - задачи, страница 2

Замечание

В строку ответа вписать через пробел номер выбранного графика и математическое ожидание.

Пример (номер графика – 1, математическое ожидание равно 3)

1 3

1 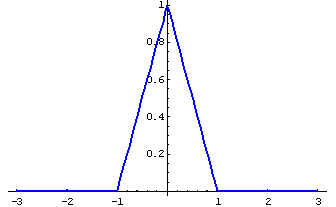(дисперсия- 1/6)

2 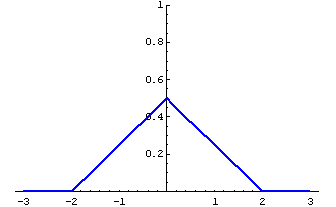(дисперсия- 2/3)

3 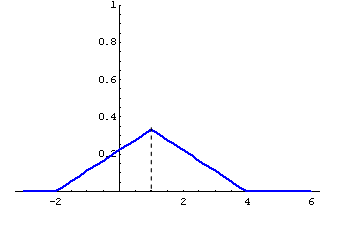3/2

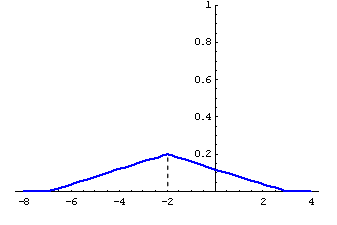4 4,167

5 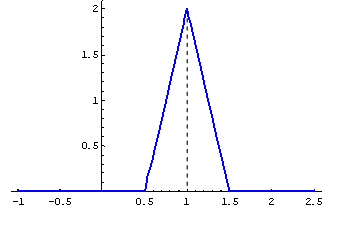0,0067

Отв 5 1

Задача 2

1.

Определить дисперсию, если случайная величина задана функцией плотности распределения вероятностей.

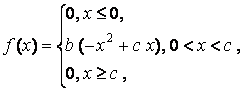
Отв 0,2

C=2a,

B=3/(4a^3)

2.

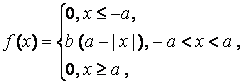
Отв0,167

b=1/a^2

7/8=0.875

3.

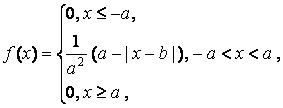
Отв a^2/6

Задача 3

Дан ряд распределения случайной величины

Найти дисперсию случайной величины .

Отв x1*p1 + x2*p2 +x3*p3+x4*p4

Задача 4

В одном ящике лежит $(m1) белых шаров и $(n1) черных шаров. В другом ящике лежит $(m2) белых шаров и $(n2) синих шаров. Пусть X – цвет шара, вынутого из первого ящика, Y – цвет шара, вынутого из второго ящика. Из каждого ящика вынули по шару. Таблица закона распределения случайных величин выглядит следующим образом