Амплитудная модуляция.
Модуляция обычно заключается в пропорциональном первичному сигналу x(t) изменении параметра переносчика. Тогда при
АМ DU=ax(t),
ФМ Dj=ax(t),
ЧМ Dw=ax(t),
Где a - коэффициент пропорциональности.
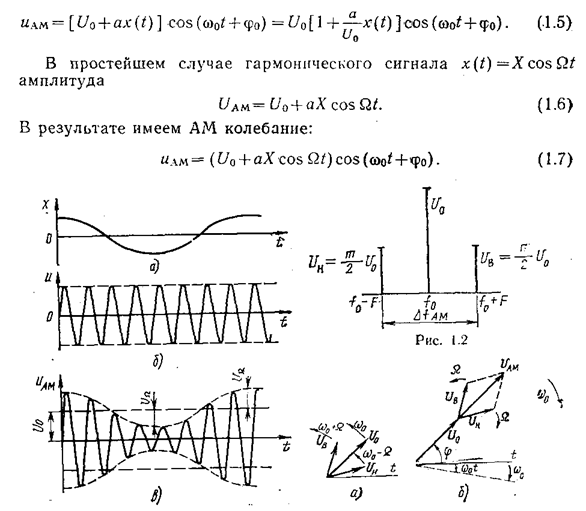
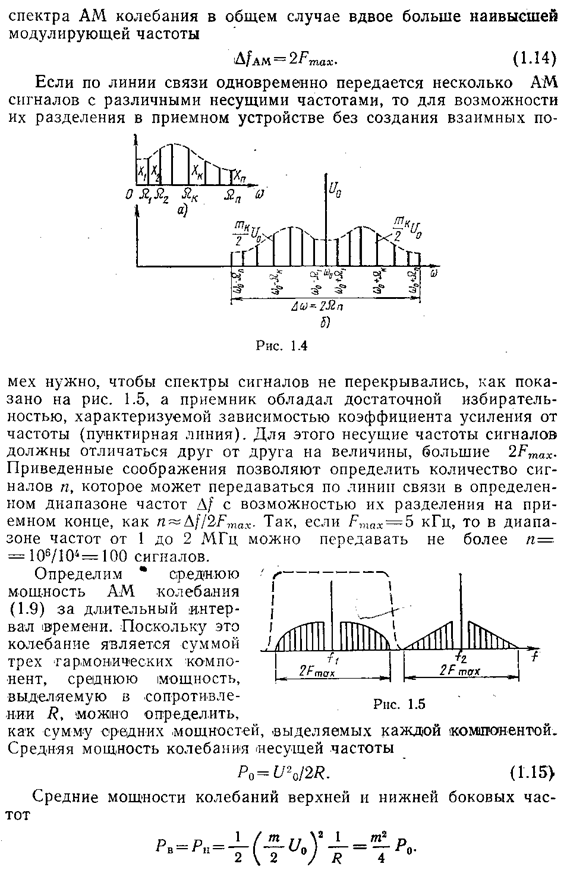
Амплитудная модуляция состоит в пропорциональном первичному сигналу x(t) изменении параметра переносчика UАМ = U0 +ax(t). В результате получается АМ колебание:
|


 |
|||||
 |
Амплитудную модуляцию можно осуществлять в нелинейных и параметрических цепях.
Ниже рассматриваются нелинейные модуляторы, имеющие более широкое распространение.
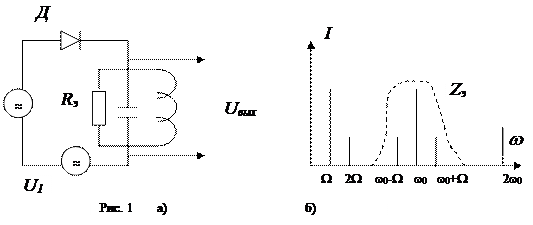
На рис. 1а) изображена схема нелинейного амплитудного модулятора, в котором в качестве нелинейного элемента применяется диод Д. На схему действуют два напряжения: высокочастотное (u1=U1 cosw0t) и низкочастотное (u2=U2 cosWt). Вольт – амперную характеристику диода ( i= F(u)) аппроксимируем полиномом второй степени
![]() (1)
(1)
Пренебрегая влиянием выходного напряжения на ток (что в данной схеме можно сделать, если эквивалентное сопротивление контура RЭзначительно меньше дифференциального сопротивления диода), имеем
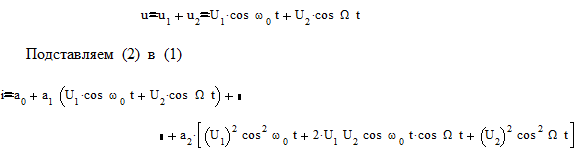
Представляя это выражение в виде суммы гармонических колебаний различных частот, строим спектр тока. В соответствии с общими правилами, спектр тока рис. 1б) содержит первые и вторые гармоники частот w0 и W и комбинационные частоты второго порядка w0 ± W. Для получения АМ колебания нужно из всего спектра выделить компоненты с частотами w0 , w0 ± W, что достигается пропусканием тока через колебательный контур, настроенный на частоту w0. Составляющие тока с частотами, близкими к w0 , определяются как
U1iw0 = a1U1 cosw0t + a2U2 U1cosw0 t× cos W t .
 |
|||
|
|||
Если характеристика Zэ(w) контура такова, что для частот w0, w0+W и w0-W Zэ @ Rэ, а для остальных компонент тока Zэ(w) @ 0, то на контуре получаем АМ напряжение
uвых = iw0 Rэ= a1 Rэ U1 (1+ (a2U2 /a1)× cos W t )× cosw0 t.
uвых = Uвых (1+ m×cos W t )× cosw0 t.
Где Uвых = a1 Rэ U1 , m=(a2U2 /a1).
Глубина модуляции (m) тем больше, чем сильнее нелинейность характеристики, определяемая (a2) , и амплитуда модулирующего сигнала (U2). Изменение огибающей АМ колебания пропорционально модулирующему сигналу (u2), поэтому модуляция оказывается неискаженной.
Если в той же схеме характеристику нелинейного
элемента аппроксимировать полиномом третьей степени ![]() , то спектр тока при входном напряжении будет
содержать уже по три гармоники частот w0 и W и
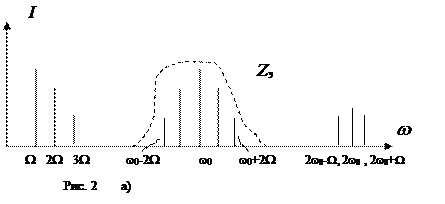
комбинационные частоты второго и третьего порядков (w0 ±W, w0 ±2W, 2w0 ± W). Этот
спектр построен на рис. 2а). Для получения неискаженной модуляции нужно, как и
прежде, поставить фильтр (например, контур), выделяющий из всего спектра тока
только компоненты частот w0 и w0 ±W. Однако , поскольку
полоса пропускания фильтра должна определятся наибольшей возможной частотой
модуляции Wмах , а в спектре модулирующего сигнала будут и частоты W, значительно меньшие Wмах
, для большинства частот W фильтр не
позволит избавится от составляющих w0
±2W. Наличие
же этих компонент означает модуляцию высокочастотного колебания частотами 2W, т.е. искажение огибающей.
, то спектр тока при входном напряжении будет
содержать уже по три гармоники частот w0 и W и
комбинационные частоты второго и третьего порядков (w0 ±W, w0 ±2W, 2w0 ± W). Этот
спектр построен на рис. 2а). Для получения неискаженной модуляции нужно, как и
прежде, поставить фильтр (например, контур), выделяющий из всего спектра тока
только компоненты частот w0 и w0 ±W. Однако , поскольку
полоса пропускания фильтра должна определятся наибольшей возможной частотой
модуляции Wмах , а в спектре модулирующего сигнала будут и частоты W, значительно меньшие Wмах
, для большинства частот W фильтр не
позволит избавится от составляющих w0
±2W. Наличие
же этих компонент означает модуляцию высокочастотного колебания частотами 2W, т.е. искажение огибающей.
 |
На практике в качестве нелинейных элементов модуляторов чаще используют не диоды, а транзисторы. Модулируемое высокочастотное напряжение подают во входную цепь нелинейного элемента. Модулирующий же сигнал вводят в цепи различных электродов: в транзисторах – в цепь базы или коллектора (соответственно базовая или коллекторная модуляция). Рассмотрим схему базовой модуляции на транзисторе (рис. 3). Напряжение на базе содержит, кроме смещения Еб, определяющего положение рабочей точки, колебания низкой и высокой частот
uб = u1 + u2 + Eб .
Здесь u1=U1 cosw0t- высокочастотное напряжение; u2=U2 cosWt - модулирующее низкочастотное напряжение. На (рис. 4а – в) по характеристике прибора iк = F( uб) методом проекций построена зависимость iк от времени. Коллекторный ток представляет последовательность импульсов, отличающихся друг от друга высотой Iмах и углом отсечки q. Если разложить каждый из этих импульсов тока в ряд Фурье за период высокой частоты T0=2p/w0, получим постоянную составляющую и гармоники высокой частоты. Напряжение на контуре, настроенном на частоту w0 , создается только первой гармоникой iк1=Iк1 cosw0t :
uвых = iк1 Rэ= Iк1×cosw0 t.
Изменение высоты и ширины импульсов тока во времени приводит к изменению амплитуды Iк1 с низкой частотой W. Поэтому выходной напряжение получается модулированным по амплитуде (рис. 4г ).
Режим работы модулятора, определяемый величинами Eб , U1 и U2 , нельзя
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.