Разработка обобщенной структурной схемы системы связи для передачи непрерывных сообщений дискретными сигналами (амплитуда канальных сигналов – 21 мВ, дисперсия шума – 67.032 мкВт)

Чтобы сделать отношение мощностей сигнала и шума одинаковым при разных амплитудах, необходим переменный шаг квантования. Для уменьшения шума квантования нужно увеличить число разрядов, поэтому следует увеличить полосу частот, но увеличивать разрядность двоичного кода – не выгодно.

3.10. Использование сложных сигналов и согласованного фильтра

Считаем, что символ “1” и “0” передаются сложными сигналами S₁(t) и S₂(t), которые представляют собой последовательности прямоугольных импульсов положительной и отрицательной полярности длительности t.

Прием этих сигналов ведется с помощью согласованного фильтра, т.е. такого, который обеспечивает потенциальную помехоустойчивость, т.е. минимальную вероятность ошибки. Преимуществом использования сигналов с большой базой является то, что повышается помехоустойчивость, т.е. вероятность ошибки уменьшается. Недостатком является уменьшение скорости передачи по каналам связи.

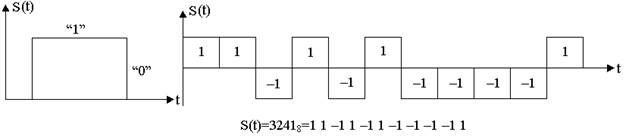3.11.  Форма сложных сигналов при передаче по каналу связи

                                            символов “1” и “0”

Изобразим сигналы S₁(t) и S₂(t) при передачи по каналу связи:

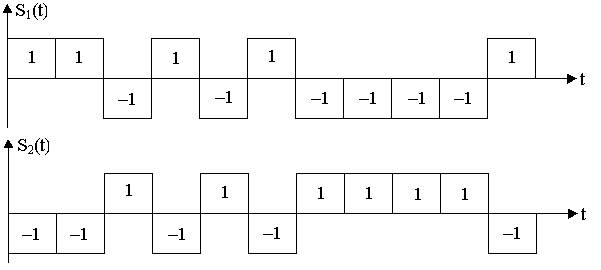
3.12.  Импульсная характеристика согласованного фильтра

Импульсная характеристика – есть отклик цепи на d-функцию.

      

         

;   ;

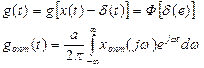
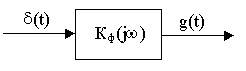
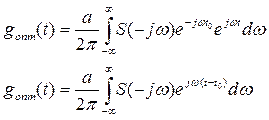
Импульсная характеристика согласованного фильтра представляет собой зеркальное отображение S(t) с точностью до некоторого постоянного множителя и со сдвигом влево на величину Т.

Основным соотношением для оптимального фильтра считают импульсную характеристику, которая является зеркальным отображением схемы.

Другие считают основным соотношением такого фильтра – это рассмотрение работы фильтра в частотной области.

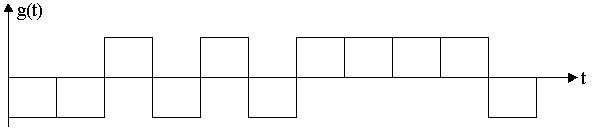
Изобразим импульсную характеристику для сигнала S₁(t)

3.13.  Схема согласованного фильтра для приема сложных сигналов

Приведем схему согласованного фильтра для заданного сигнала

1 1 –1 1 –1 1 –1 –1 –1 –1 1

1)  при синхронном способе приема

При приеме, последовательность импульсов продвигается по линии задержки и в момент, когда все отрицательные импульсы совпадают по знаку с цифровым инвертором. Все импульсы складываются, на выходе решающего устройства (РУ) появляется импульс – согласованный фильтр зафиксирует данную комбинацию. При двух сдвигах изолирование производится не в фазе и на выходе РУ появляются максимальные уровни.

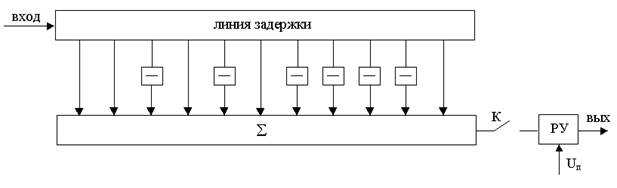Оптимальный фильтр, построенный по синхронной схеме, используется при точно известных комбинациях.

Причем, U_п=0, т.к. значения побочных максимумов не влияет на выносимое решение.

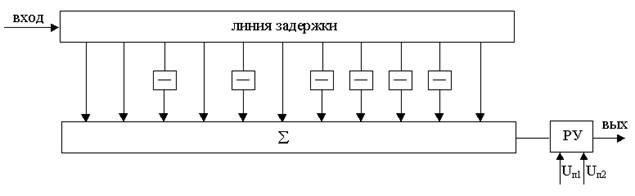
2) при асинхронном приеме

При асинхронном методе расчитываются U_пор, т.к. на вход согласованного фильтра поступают сигналы “1” и “0”, из-за чего появляются дополнительные максимумы.

3.14.  Форма сигналов на выходе согласованного фильтра при передаче сигналов “1” и “0”

Расчитаем форму сигнала на выходе согласованного фильтра при передаче “1”.

Изобразим форму этого сигнала, кодовая последовательность которого :

1 1 –1 1 –1 1 –1 –1 –1 –1 1

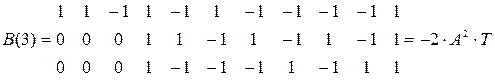
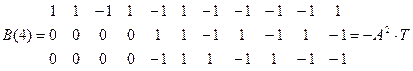
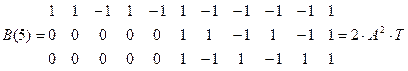
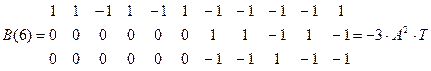
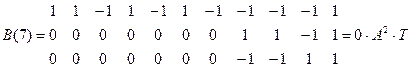
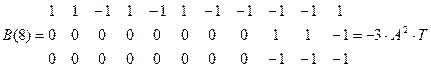
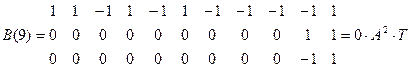
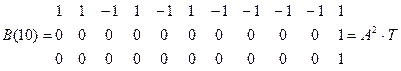
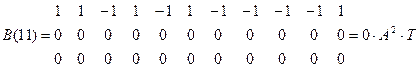
t\с	1	1	-1	1	-1	1	-1	-1	-1	-1	1	В(t)
11	1	1	-1	1	-1	1	-1	-1	-1	-1	1	11
10		1	1	-1	1	-1	1	-1	-1	-1	-1	-4
9			1	1	-1	1	-1	1	-1	-1	-1	3
8				1	1	-1	1	-1	1	-1	-1	-2
7					1	1	-1	1	-1	1	-1	1
6						1	1	-1	1	-1	1	-4
5							1	1	-1	1	-1	3
4								1	1	-1	1	-2
3									1	1	-1	1
2										1	1	0
1											1	-1
0											0	0

В(-t) будет симметричен относительно оси В(t). При передаче “0” на выходе согласованного фильтра будет сигнал симметричный сигналу при передаче “1” относительно оси t.

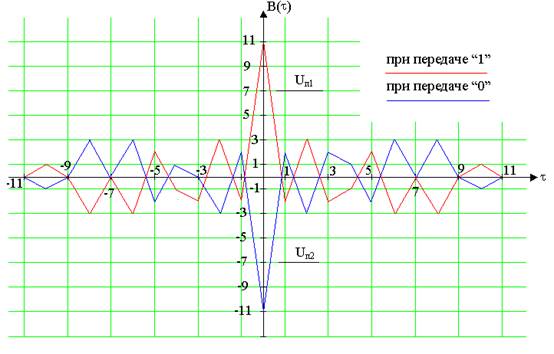Форма сигнала на выходе согласованного фильтра при переходе сигнала “1” соответствует виду функции корреляции, сдвинутой на длительность сигнала 11t. Форма сигнала при передаче “0” симметрична форме сигнала при подаче “1” относительно временной оси t.

3.15.  Оптимальные пороги при синхронном и асинхронном способах приема сигналов в схеме с согласованным фильтром

Расчитаем оптимальные значения порогов и нанесем их на график для синхронного и асинхронного способов приема.

Для схемы с синхронным приемом U_п=0, т.к. значения побочных максимумов не влияют на выносимое решение. Но при асинхронном способе приема , потому что возможно ложное