Разработка устройств цифрового формирования и обработки сигналов системы передачи дискретных сообщений по частотно ограниченным каналам связи (удельная скорость передачи – 2,5 бит∙с/Гц, разрядность ЦАП – 6, вид модуляции – ФМ на поднесущих)

Прием  решения  можно  производить   в   средней,   наименее искаженной  части  сигнала.  Для  уменьшения  межканальных   искажений  поднесущие    должны  быть  ортогональны   на   длительности  элементарного  сигнала .

Условие  ортогональности сигналов может быть записано в следующем виде:

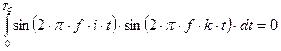         ,  если  [3,стр.270]         (2.24)

Если в сигналах будут присутствовать помехи, то условие ортогональности выполняться не будет.

Поскольку используется передача на поднесущих частотах, то можно записать  аналитические выражения сигналов используемых для передачи:

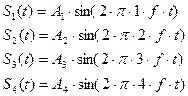           [3, стр.268]          (2.25)           где А_i-амплитуда сигнала.

Пусть нам требуется передать двоичную последовательность 00101101. Количество информации, переносимое элементарным сигналом, определяется выражением:

, где N – число элементарных сигналов

N = 4 следовательно каждый сигнал несет 2 Бит.

Разобьем данную последовательность на 4 пары: 00, , 10, 11,01.

Пусть последовательность 00 будет передаваться сигналом S₁, 10-S₂, 11-S₃, 01-S₄.

Графически формирование выходного сигнала изображено на рисунках 2.6, 2.7

Таблица 2.1 – Отсчеты сигнала S₁(t) во временной области

	0	0.0625	0.125	0.1875	0.25	0.3125	0.375	0.4375
	0	0.383	0.707	0.924	1	0.924	0.707	0.383
0.5	0.5625	0.625	0.6875	0.75	0.8125	0.875	0.9375	1
0	-0.383	-0.707	-0.924	-1	-0.924	-0.707	-0.383	0

Таблица 2.2 – Отсчеты сигнала S₂(t) во временной области

	0	0.0625	0.125	0.1875	0.25	0.3125	0.375	0.4375
	0	0.707	1	0.707	0	-0.707	-1	-0.707
0.5	0.5625	0.625	0.6875	0.75	0.8125	0.875	0.9375	1
0	0.707	1	0.707	0	-0.707	-1	-0.707	0

Таблица 2.3 – Отсчеты сигнала S₃(t) во временной области

	0	0.0625	0.125	0.1875	0.25	0.3125	0.375	0.4375
	0	0.924	0.707	-0.383	-1	-0.383	0.707	0.924
0.5	0.5625	0.625	0.6875	0.75	0.8125	0.875	0.9375	1
0	-0.924	-0.707	0.383	1	0.383	-0.707	-0.924	0

Таблица 2.4 – Отсчеты сигнала S₄(t) во временной области

	0	0.0625	0.125	0.1875	0.25	0.3125	0.375	0.4375
	0	1	0	-1	0	1	0	-1
0.5	0.5625	0.625	0.6875	0.75	0.8125	0.875	0.9375	1
0	1	0	-1	0	1	0	-1	0

Изобразим отсчеты сигнала на длительности сигнала между двумя характеристическими моментами восстановления, условившись, что  (рисунок 2.1).

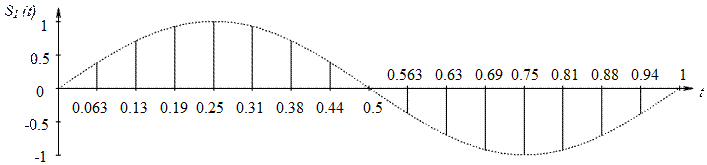
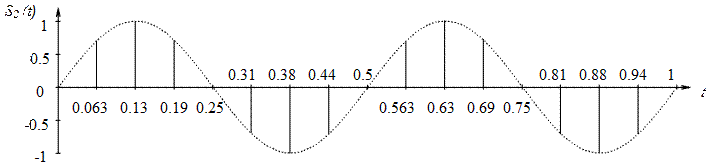
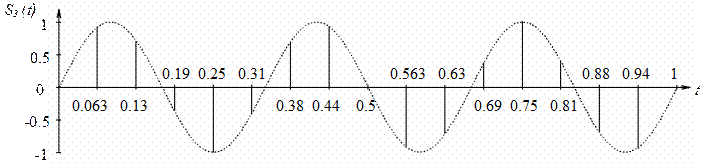
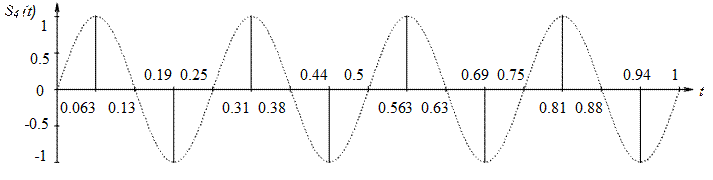 Рисунок 2.4 – Отсчеты сигнала на длительности сигнала между двумя характеристическими моментами восстановления

Рассчитаем суммарные отсчеты сигнала на длительности между двумя характеристическими   моментами восстановления. Результаты сведем в таблицу 2.5

Таблица 2.5 – Суммарные отсчеты на длительности между двумя моментами восстановления

	0	0.0625	0.125	0.1875	0.25	0.3125	0.375	0.4375
	0	3.014	2.414	0.248	0	0.834	0.414	-0.401
0.5	0.5625	0.625	0.6875	0.75	0.8125	0.875	0.9375	1
0	0.401	-0.414	-0.834	0	-0.248	-2.414	-3.014	0

По результатам вычислений построим суммарные отсчеты сигналов (рис. 2.5).

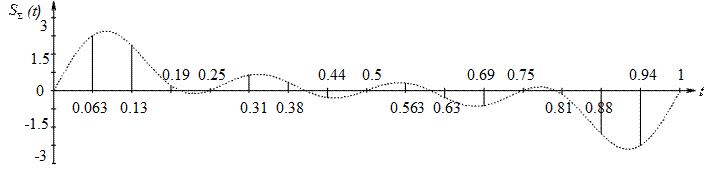 Рисунок 2.5 – Суммарные отсчеты сигнала

С учетом того, что каждая поднесущая модулируется сигналом вида , то  графически формирование выходного сигнала будет выглядеть как показано на рисунках

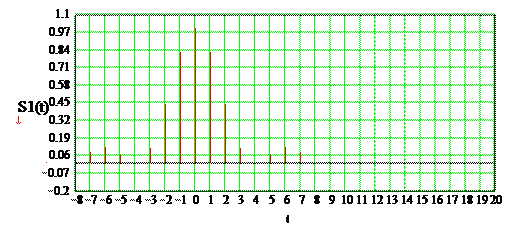
Рисунок 2.6 – Отсчеты сигнала S₁

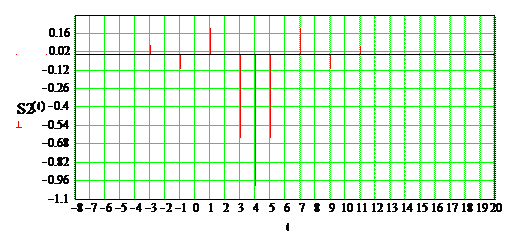
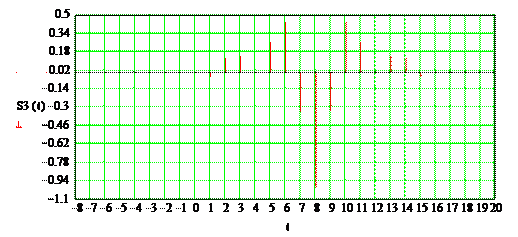
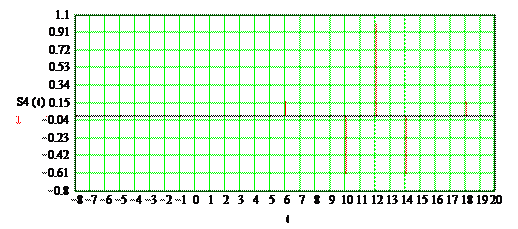
По результатам вычислений построим суммарные отсчеты сигналов (рис. 2.7).

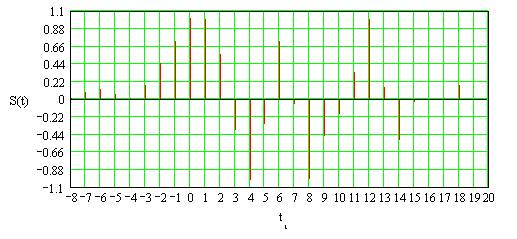
 Рисунок 2.7 – Суммарные отсчеты сигнала

Учитывая, что сигнал на выходе цифрового формирователя определяется суммированием только четырех отсчетов на каждом элементе и на том элементе, где присутствуют одновременно все четыре сигнала, то выдаваться будут только отсчеты 4,5,6,7 из суммы отсчетов. Причем эти отсчеты будут квантованными (в соответствии с разрядностью ЦАПа). .

2.6 Спектр сигнала на выходе цифрового формирователя

Расчет спектров дискретных сигналов производится с использованием дискретного преобразования Фурье по формуле:

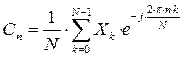                                     .                                                  (2.26)

Количество отсчетов в спектральной области С₀, С₁, …, С_N-1 равно количеству отсчётов сигнала X₀, X₁, …, X_K-1 взятых во временной области.  N – это количество отсчётов.

Для расчета спектра сигнала воспользуемся программой DPF.EXE (Лабораторная работа №3).

Таблица 2.6– Амплитуда и фаза отсчетов в спектральной области

Xk	0	3.014	2.414	0.248	0	0.834	0.414	-0.401
Cn	0	0.545	0.511	0.415	0.24	0.286	0.178	0.147
Qn	0	-79.41	-68.82	-58.24	-47.65	-3706	-26.47	-15.88
0	0.401	-0.414	-0.834	0	-0.248	-2.414	-3.014	0
0.136	0.136	0.147	0.178	0.286	0.24	0.415	0.51	0.545
-5.29	5.29	15.88	26.47	37.06	47.65	58.24	68.82	79.41

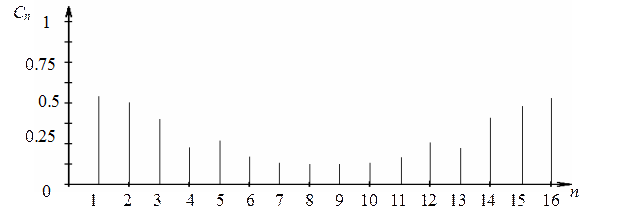
Рисунок 2.8– Амплитудный спектр

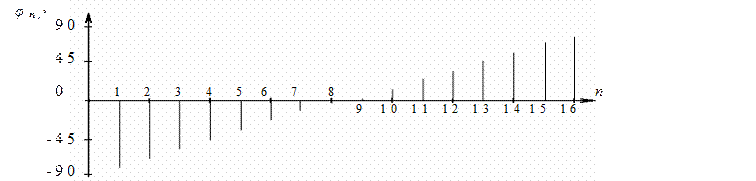
Рисунок 2.9– Фазовый спектр

Спектр сигнала вида   рассчитывается по формуле:

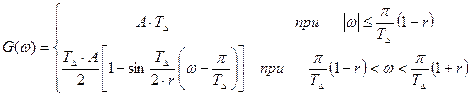       [4]      (2.27)

С учетом того, что в данной работе r =0,6 и примем А=1, получаем

  

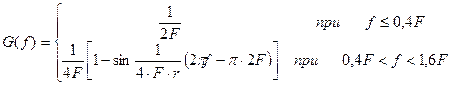
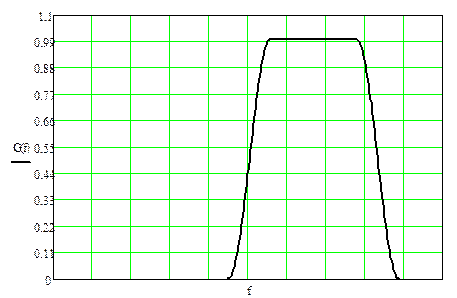
Спектр на выходе  формирователя,  и полосового фильтра представлен на рисунке 2.10.

Рисунок 2.10– Спектр сигнала на выходе  формирователя

2.7 Расчет мощности шума квантования на выходе цифрового формирователя сигнала

Основным недостатком цифровой обработки сигналов является наличие шумов квантования. Поэтому при расчете любой аппаратуры ЦОС необходимо учитывать шум квантования, так как он может приводить к ошибкам при передачи информации.

Шум квантования целиком и полностью определяется выбором уровней квантования, то есть разрядностью ЦАП.

Шум квантования рассчитывается по формуле:

, где ,

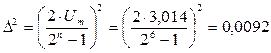, мВт.

Для уменьшения шума квантования можно увеличить разрядность ЦАП, но это приведет к увеличению стоимости аппаратуры.

.

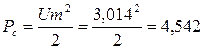Значение отношения «сигнал/шум»  или 37,75 дБ, что вполне достаточно для надежного определения решения на приеме.

2.8 Функциональная схема устройства цифрового формирования

Функциональная схема устройства цифрового формирования представлена на рисунке 2.11. 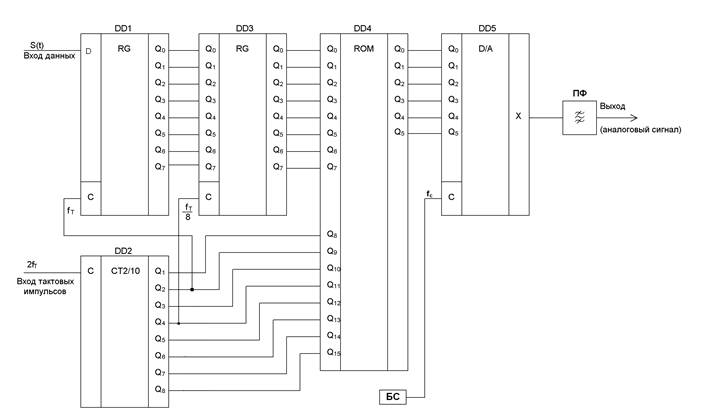            Рисунок 2.11 – Функциональная схема устройства цифрового формирования

На вход сдвигового регистра DD1 подается последовательная комбинация