Определение потокораспределения в линиях с двухсторонним питанием

8.2. Определение потокораспределения  в линиях

с двухсторонним питанием

          Возможны различные варианты работы электрической сети, как линии с двухсторонним питанием (рис.8.3). Простейшая кольцевая электрическая сеть (рис.8.3, а) превращается в линию с двухсторонним питанием при условном разрезании ее по источнику питания. Характерным в этом случае считается равенство напряжений  по концам линии .Другим примером линии с двухсторонним питанием является часть сети, связывающая электростанцию с электрической системой (рис.8.3, б) или две системы друг с другом (рис.8.3, в). В этих случаях напряжения на шинах электростанции и системы или разных систем, как правило, различны  .

На рис.8.3, г приведен вариант линии, связывающей  две системы, но с ответвлением на участке ij от магистрали. Такая сеть для расчета линии с двухсторонни питанием приводится к варианту, аналогичному рис.8.3, в. При этом нагрузка узла j приводится к узлу i с учетом потерь мощности на участке ij и зарядной мощности его и суммируется с нагрузкой узла i. При расчете потокораспределения во всех рассматриваемых вариантах характерным является то, что заданными являются напряжения по концам линии и мощности (или токи) нагрузки в промежуточных точках линии. Фактически расчет потокораспределения в линиях с двухсторонним питанием включает два этапа:

 - без учета потерь мощности на участках линии;

            -  с учетом потерь мощности.

Определение потокораспределения без учета потерь мощности. Пусть задана линия с двухсторонним питанием, в которой нагрузка узлов представлена в виде комплексных значений токов  (рис.8.4). Известны также сопротивления участков линии  и напряжения  на шинах источников питания, т.е. по концам линии   и . Направим токи на участках произвольно так, как указано на схеме. В соответствии со вторым законом Кирхгофа запишем следующее уравнение

                               -=(           ( 8.1)

Заметим, что при =  оно примет вид

                             (=0                      (8.2)

          По первому закону Кирхгофа выразим токи на участках линии через заданные токи в узлах нагрузки   и ток , вытекающий из источника А:

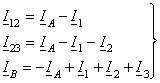                                                          (8.3)

          Подставим значения токов из выражений (8.3) в (8.1):

Сгруппируем члены, содержащие одинаковые токи

Отсюда

                                    ,                               (8.4)

где   ;

         ;

        

В общем случае, когда к линии  с двухсторонним питанием  с источниками  в точках А и В подключены нагрузки в  n узлах, последнее выражение примет вид

                                                                                        (8.5)

где  - ток нагрузки в i-ом узле;  - сопротивление от i-ого узла до источника питания В.

Аналогичным образом для тока  источника питания В можно получить

                                     =                                           (8.6)

Первый член в выражении (8.5) представляет собой сквозной уравнительный ток

                                              (8.7)

Он обусловлен разностью напряжений источников и сопротивлением всей линии между ними.

Если  =, то  =0  и выражения (8.5) и  (8.6)  принимают вид

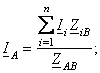
                                                                     (8.8)

Как отмечалось, равенство напряжений источников   характерно для кольцевой замкнутой сети (рис.8.3, а), следовательно для нее и справедливы выражения (8.8).

Рассмотрим случай, когда нагрузки в узлах заданы мощностями. Фактически ток и мощность в любом узле связаны формулой

Так как напряжения в узлах нагрузки не известны, то примем их одинаковыми и равными номинальному .

Если формулы (8.5) и (8.6) преобразовать относительно определения сопряженных комплексов тока  и  и умножить левые и правые части полученных выражений на  , то получим формулы для расчета мощностей, отдаваемых в линию источниками А и В:

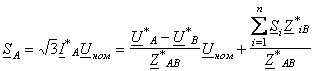;                        (8.9)

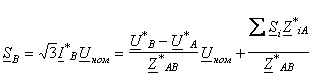                       ,                        (8.10)   

где    и   - соответственно сопряженные комплексы напряжения и сопротивления;    - мощность нагрузки сети в  i-ом узле.

          Переход от строгих выражений для токов (8.5), (8.6) к выражениям для мощностей (8.9), (8.10) осуществлен с допущением, что напряжения во всех точках сети одинаковы. Это является основанием того, что расчет по формулам (8.9) и (8.10)  позволяет найти потоки мощности  источников  без учета потерь мощности  на участках линии. Сумма этих мощностей должна быть равна сумме мощностей нагрузок в узлах

Последнее уравнение является условием проверки правильности нахождения мощностей  и .

          Первая составляющая выражений  (8.9) и (8.10)  представляет сквозную уравнительную мощность, протекающую на всех участках между точками А и В вследствие их различных напряжений

                                                                                            (8.11)

Если   , то   и формулы  (8.9) и  (8.10)  принимают вид

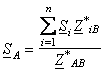                                                    ;                                                (8.12)

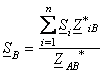                                                     ;                                               (8.13)

Сравнение выражений (8.9), (8.10) с (8.11), (8.12), (8.13) дает основание применить для расчета потокораспределения без учета потерь мощности при различных напряжениях источников известный метод наложения. Согласно ему, потоки мощности в исходной линии (рис.8.5, а) можно получить в результате наложения (суммирования) потоков мощности, определенных по формуле (8.12), (8.13), в линии с равными напряжениями  по концам источников  согласно рис.8.5, б  и сквозной уравнительной мощности , найденной по формуле (8.11), в соответствии со схемой, приведенной на рис.8.5, в.

          Линию с двухсторонним питанием, в которой все участки между источниками выполнены проводом одного сечения с одинаковыми расстояниями и расположением проводов  между фазами, называют однородной. В ней для каждого участка   . Поэтому для однородной линии при         выражения  (8.12), (8.13) можно представить в виде

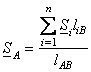 =;                   (8.14)                                                        

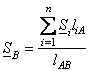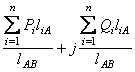  =;                           (8.15)

Последние выражения показывают, что в однородных линиях распределение активных и реактивных мощностей не зависят друг от друга.

По найденным значениям ,  и мощностям узлов нагрузок, исходя из первого закона Кирхгофа на основе уравнений, аналогичных (8.3), можно найти потоки мощности на всех участках линии. Так, мощность на участке 12

Допустим, что в результате расчета потокораспределения направления потоков мощности на участках оказались такими, как указано на рис 8.5, а. Здесь узел 3 получает питание от двух источников А и В. Узел сети, нагрузка которого питается с двух сторон, называется точкой потокораздела.

Расчет потокораспределения с учетом потерь мощности. Пусть в результате расчета потокораспределения без учета потерь мощности получены направления и значения потоков мощности на участках, нанесенные на рис. 8.6, а. Как видно, узел 2 является точкой потокораздела активных и реактивных мощностей. При правильном определении нанесенных мощностей

или

Поэтому найденные мощности на участках вблизи точки потокораздела можно принять за действительные потоки мощности в конце этих участков (рис.8.6, б)

;

Исходную схему можно представить в виде двух разомкнутых, разрезав ее по узлу 2 (рис.8.6, б). Таким образом дальнейший расчет фактически сводится к расчету потокораспределения в разомкнутых  сетях при заданных напряжениях источников  А и В и мощностях в узлах нагрузки. По мощности  и номинальному напряжению находят потери мощности на участке 12    и с их учетом мощность в начале этого участка    (рис.8.6, в)

;

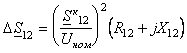          По первому закону Кирхгофа для узла 1 определяют  и так далее.

На рис. 8.6, г  представлен случай, когда в результате расчета потокораспределения без учета потерь мощности точки потокораздела активных и реактивных мощностей не совпадают. Здесь узел 2 - точка потокораздела активной мощности, а узел 1 - реактивной.

          В данном случае линия с двухсторонним питанием также может быть разделена на две разомкнутые. Для этого находят предварительно потери мощности на участке между точками потокораздела

Затем составляют две разомкнутые сети (рис.8.6, д) без участка между точками потокораздела 1 и 2.  При этом нагрузка  в точке потокораздела  активных мощностей 2 (рис.8.6, д) включает мощность участка 32, найденную без учета потерь мощности,    и потери реактивной мощности    между точками потокораздела

Нагрузка  в точке потокораздела реактивных мощностей 1 состоит из мощности участка А1, определенной без учета потерь мощности  и потерь активной мощности      между точками потокораздела

Дальнейший расчет сводится фактически к расчету разомкнутых сетей (рис.8.6, д).