Построение эпюр изгибающих моментов поперечных сил

12.6. Построение эпюр изгибающих моментов М_и  поперечных сил Q.

Пример 1. Построить эпюры изгибающих моментов М_и  поперечных сил Q для балки, нагруженной силой Р (рис.39).

Рис.39

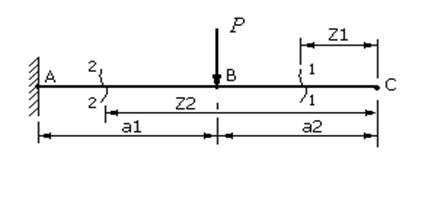
Для определения значений внутренних силовых факторов (изгибающих моментов и поперечных сил) используем метод сечений. Проводим сечение 1-1 на расстоянии z₁ от правого конца балки (справа от точки приложения силы P). Поскольку справа от сечения на балку не воздействуют ни внешние силы, ни внешние пары, то очевидно, что сумма моментов справа от сечения равна нулю.

Следовательно, на участке балки В-С изгибающий момент .

Проводим на расстоянии z₂ сечение 2-2 на участке балки А-В и определяем изгибающий момент как сумму моментов всех внешних сил справа от сечения:

  при . Знак минус, поскольку балка изгибается выпуклой частью вверх (момент внешних сил справа от сечения действует по часовой стрелке).

Получили уравнение наклонной прямой линии. Для построения эпюры изгибающих моментов вычислим два значения M_и:   при z₂=a₂ и  при z₂=a₁ + a₂. Величину  в выбранном масштабе откладываем вниз от оси эпюры и полученную точку соединяем с нулевой в т. z₂=a₂ .

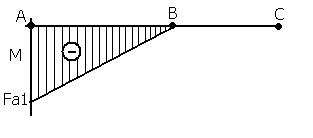
Из эпюры изгибающих моментов видно, что максимальный изгибающий момент возникает у заделки .

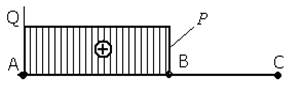
Для построения эпюры поперечных сил проецируем на вертикальную ось силы, расположенные справа от сечения 1-1, получаем  . Для сечения 2-2 по аналогии получим  .

Знак «+» потому, что внешняя сила справа от сечения направлена сверху вниз, или потому, что при движении слева направо эпюра М восходящая.

Пример 2. Построить эпюры М_и (изгибающих моментов) и поперечных сил Q для консольно закреплённой балки (рис.40), нагруженной распределенной нагрузкой q.

Рис.40

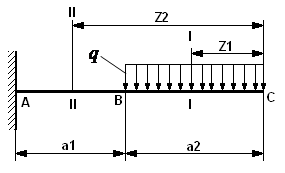Рассмотрим участок В-С балки, нагруженной распределённой нагрузкой q.  Сделаем сечение I-I на расстоянии z₁ от конца балки C на участке действия распределённой нагрузки q. Величину изгибающего момента определим, заменив распределённую нагрузку q её равнодействующей q* z₁, приложенной к середине участка z₁:

 при

Знак минус указывает на то, что при изгибе у балки выпуклость сверху. Для построения эпюры изгибающих моментов необходимо определим хотя бы три точки (в начале, в середине и в конце участка В-С):

при z₁ =0  -                                                ;

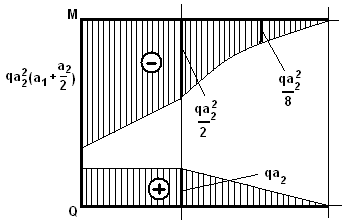
при z₁ =a₂ /2  -                                            ;

при z₁ =a₂  -                                               .

В выбранном масштабе строим эпюру изгибающих моментов для участка В-С.

Делаем сечение на расстоянии z₂ для участка А-В. Распределённую нагрузку q на длине a2 заменяем её равнодействующей , приложенной к середине участка В-С.

Изгибающий момент в сечении II-II: . Это уравнение прямой. Для её построения определим две точки: при - получим   и при   соответственно получим -  .

Поперечная сила в сечении I-I определяется как сумма проекций на вертикаль правых от сечения сил:

  (соответственно, при z1=0 -     Q=0, а при z1=a2 -      Q=q*a2).

Поперечная сила в сечении II-II: Q=q*a2. Знак «+» поскольку M восходящая при движении слева направо (равнодействующая внешних сил справа от сечения направлена сверху вниз).

С другой стороны, по формуле Журавского:  , поэтому можно записать:  (соответственно, при z1=0 -     Q=0, а при z1=a2 -      Q=-q*a2). В этом случае требуется изменить знак минус на плюс, поскольку по правилу знаков поперечная сила должна быть положительной.

По результатам проведенных расчетов и с учетом формул Журавского можно сделать следующие выводы:

·  для тех участков балки, где изгибающий момент изменяется по параболической зависимости (кривая второго порядка), поперечная сила изменяется по линейному закону, т.е. эпюра Q – наклонная прямая;

·  для тех участков балки, где изгибающий момент изменяется по линейному закону, т.е. эпюра изгибающих моментов – наклонная прямая, поперечная сила постоянна (эпюра поперечной силы – горизонтальная прямая, т.е. линия нулевого порядка);

·  в точках максимума или минимума эпюры изгибающего момента поперечная сила равна нулю.