5.4. Методы определения потерь электроэнергии в электрических сетях
Потери электроэнергии - это есть потери мощности за какой-то промежуток времени. Величина потерь существенно зависит от характера изменения нагрузки в течение этого периода времени.
В элементе электрической
сети, работающем с неизменной нагрузкой и имеющем потери активной мощности ![]() , потери электроэнергии за время
, потери электроэнергии за время ![]() составят
составят
![]() . (5.25)
. (5.25)
В действительности нагрузки элементов сети не остаются постоянными, а изменяются в соответствии с графиками нагрузки потребителей, режимами работы отдельных электростанций.
В общем случае потери
электроэнергии в элементе электрической сети с неизменными сопротивлением ![]() и напряжением
и напряжением ![]() за промежуток времени
за промежуток времени ![]() составят
составят
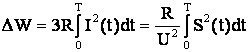 , (5.26)
, (5.26)
где ![]() ,
, ![]() - соответственно протекающие по
элементу сети ток и мощность в момент времени
- соответственно протекающие по
элементу сети ток и мощность в момент времени ![]() .
.
Расчет
потерь электроэнергии по формуле (5.26) требует знания закона изменения тока
или мощности во времени. Однако в общем случае этот закон математическому
описанию не поддается. Поэтому для учета изменения тока или мощности во времени
применяют различные математические и алгоритмические приемы, позволяющие
упростить определение значения интеграла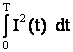 или
или 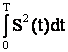 . Они определяют погрешность методов и ограничивают
область их применения.
. Они определяют погрешность методов и ограничивают
область их применения.
Метод графического
интегрирования основан на знании графика нагрузки (рис.5.4). Весь
промежуток времени ![]() делится на
делится на ![]() равных частей длительностью
равных частей длительностью ![]() . Каждому
. Каждому ![]() - му промежутку времени соответствует определенное значение
тока
- му промежутку времени соответствует определенное значение
тока ![]() или мощности
или мощности ![]() . Выполнив интегрирование графическим
путем, получим
. Выполнив интегрирование графическим
путем, получим
![]() . (5.27)
. (5.27)
Данный метод обладает высокой точностью, но весьма трудоемок. Он хорошо реализуется при расчетах потерь электроэнергии за небольшой промежуток времени, например, по суточным графикам нагрузки. Однако оценка потерь электроэнергии за большой промежуток времени на основании найденных потерь по характерным суточным графикам не обеспечивает нужной точности, так как режимные параметры характерных суток не являются неизменными на протяжении всего периода. Тем не менее, иногда пользуются этим методом для вычисления годовых потерь энергии, применяя формулу
![]() ,
,
где ![]() - соответственно число зимних и
летних суток в году, для условий Республики Беларусь можно принять
- соответственно число зимних и
летних суток в году, для условий Республики Беларусь можно принять ![]() и
и ![]() - потери электроэнергии за
характерные зимние и летние сутки.
- потери электроэнергии за
характерные зимние и летние сутки.
Метод
среднеквадратичного тока базируется на введении понятия условного
неизменного тока ![]() , который называется среднеквадратичным
(рис.5.5, а). При протекании его по элементу сети за время
, который называется среднеквадратичным
(рис.5.5, а). При протекании его по элементу сети за время ![]() в нем выделяются такие же потери электроэнергии, что и при
протекании за это же время действительного тока в соответствии с графиком
нагрузки. На рис. 5.5, а эти потери энергии в определенном масштабе
соответствуют площадкам оабв и огдв. На основании этого определ
ения можно записать соотношение
в нем выделяются такие же потери электроэнергии, что и при
протекании за это же время действительного тока в соответствии с графиком
нагрузки. На рис. 5.5, а эти потери энергии в определенном масштабе
соответствуют площадкам оабв и огдв. На основании этого определ
ения можно записать соотношение
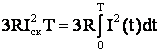 ,
,
откуда
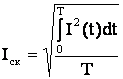 . (5.28)
. (5.28)
Исходя из метода
среднеквадратичного тока, потери электроэнергии в сопротивлении ![]() за промежуток времени
за промежуток времени ![]() можно найти по формуле
можно найти по формуле
![]() . (5.29)
. (5.29)
Если расчет выполняется в мощностях, то используют аналогичное понятие среднеквадратичной мощности
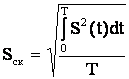 .
.
Тогда годовые потери энергии определяются в виде
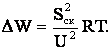
При нахождении среднеквадратичного тока используют ряд приемов, которые определяют точность данного метода расчета потерь электроэнергии.
Среднеквадратичный ток можно найти по суточному ступенчатому графику нагрузки, аналогичному рис. 5.4, с длительностью ступени, например, 1 час
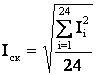 . (5.30)
. (5.30)
Тогда потери электроэнергии
![]() ,
,
что соответствует формуле (5.27). Значит, расчет среднеквадратичного тока по графику нагрузки эквивалентен расчету потерь методом графического интегрирования и имеет те же недостатки.
В практике расчетов для
типовых графиков нагрузки величину ![]() находят по наибольшему току
находят по наибольшему току ![]() ,используя эмпирическую формулу А.М.Залесского
,используя эмпирическую формулу А.М.Залесского
![]() . (5.31)
. (5.31)
Здесь ![]() - время использования наибольшей
нагрузки, определение которого дано в § 4.8. Значение
- время использования наибольшей
нагрузки, определение которого дано в § 4.8. Значение ![]() , найденное по данной формуле, можно использовать только при
расчете годовых потерь электроэнергии. При этом наибольший ток можно определить
по количеству активной
, найденное по данной формуле, можно использовать только при
расчете годовых потерь электроэнергии. При этом наибольший ток можно определить
по количеству активной ![]() и реактивной
и реактивной ![]() электроэнергии, переданной за год
электроэнергии, переданной за год
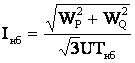 . (5.32)
. (5.32)
Среднеквадратичный ток
также можно рассчитать по среднему току ![]() (см. рис. 5.5, а) и
коэффициенту формы графика нагрузки
(см. рис. 5.5, а) и
коэффициенту формы графика нагрузки ![]() , определяемому выражением (4.43)
, определяемому выражением (4.43)
![]() . (5.33)
. (5.33)
Здесь величина среднего
тока за время ![]() равна
равна
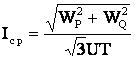 . (5.34)
. (5.34)
Значения величин ![]() и
и ![]() в формулах (5.31) и (5.33) носят
вероятностный характер. Поэтому результаты расчета потерь электроэнергии по
найденным с их использованием значениям
в формулах (5.31) и (5.33) носят
вероятностный характер. Поэтому результаты расчета потерь электроэнергии по
найденным с их использованием значениям ![]() определяются достоверностью задания
величин
определяются достоверностью задания
величин ![]() и
и ![]() .
.
Определять потери электроэнергии по среднеквадратичному току, вычисленному по формулам (5.31) и (5.33), рекомендуют в радиальных распределительных сетях.
Метод времени
максимальных потерь. Согласно ему потери электроэнергии в сопротивлении ![]() определяются по потерям мощности
определяются по потерям мощности ![]() , найденным для наибольшей нагрузки
, найденным для наибольшей нагрузки
![]() . (5.35)
. (5.35)
Здесь время максимальных потерь ![]() - есть условное время, в течение которого в элементе сети,
обладающем сопротивлением
- есть условное время, в течение которого в элементе сети,
обладающем сопротивлением ![]() и работающем с наибольшей нагрузкой,
выделялись бы такие же потери электроэнергии, что и при работе по
действительному графику нагрузки в течение года (Т=8760 ч).
и работающем с наибольшей нагрузкой,
выделялись бы такие же потери электроэнергии, что и при работе по
действительному графику нагрузки в течение года (Т=8760 ч).
В соответствии с рис.5.5, б
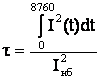 . (5.36)
. (5.36)
Аналогично можно записать выражение для τ через мощность:
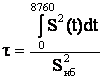 .
.
При этом предполагается, что
связь между графиками активной и реактивной мощности в течение всего
рассматриваемого периода определяется постоянным значением коэффициента
мощности ![]() .
.
Определение времени максимальных потерь по формуле (5.36) нерационально, так как в этом случае расчет потерь электроэнергии сводится к разновидности метода графического интегрирования.
В практических расчетах для типовых графиков время максимальных потерь часто рассчитывают по формуле В.В.Кезевича
![]() . (5.37)
. (5.37)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.