Мосты и трубы. Строительные нормы и правила

Расчетное внутреннее давление в дополнительном сочетании нагрузок принято с коэффициентом 1.

Наиболее невыгодным для работы трубопровода будет дополнительное сочетание нагрузок, т.е. при действии кратковременной нагрузки от транспорта.

Расчет трубы на трещиностойкость в стадии эксплуатации

Определение геометрических характеристик расчетного продольного сечения стенки трубы.

Принимаем s=22 - шаг навивки напрягаемой спиральной арматуры, мм (п. 7.8); d=5 мм -диаметр напрягаемой спиральной арматуры, мм.

Площадь напрягаемой спиральной арматуры, см²/см, в расчетном сечений трубы определяем по формуле

  (46)

где f_a = 0,196 - площадь сечения, см², арматурной проволоки диаметром 6 мм.

Коэффициент армирования продольного сечения трубы определяем по формуле

  (47)

В данном случае: b = 1 - расчетная ширина продольного сечения стенки трубы, см; h=7,5 - толщина стенки, см.

Площадь приведенного сечения определяем по формуле

F_nc = bh(1+n)     (48)

где n  = М _i == 5,56.- отношение модуля упругости арматуры к начальному модулю упругости бетона.

В данном случае: Е_л = 2* 10⁶ - модуль упругости арматуры, кгс/см² (табл. 29 СНиП П-21-75); Е₆ = 0,36 * 10⁶ - начальный модуль упругости бетона, кгс/см² (табл. 18 СНиП П-21-75).

Подставляем численные значения а формулу (48), получаем

F_n._c= 1 * 7,5(1+5,56 * 0,0119) = 8 см²/см.

Статический момент продольного приведенного сечения относительно его внутренней грани определяем по формуле

 (49)

Принимаем а’ -1,8 - расстояние от наружной грани бетона до центра тяжести напрягаемой спиральной арматуры, см.

Подставив значения в формулу (49), получаем

+ 5,56 * 0,0891 (7,5 - 1,8) = 30,95 см³ /см.

Расстояние от внутренней грани продольного приведенного сечения до его центра тяжести определяем по формуле

 (50)

Момент инерции продольного приведенного сечения относительно проходящей через его центр тяжести, определяем по формуле

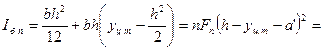
=.(51)

Момент сопротивления продольного приведенного сечения стены трубы для внутренней грани с учетом пластической работы бетона определяем по формуле, приведенной в п. 5.7

W_Т=1,75W₀,           (52)

где W₀ - момент сопротивления продольного приведенного сечения трубы для рассматриваемой грани, определяемый по формуле

 (53)

Подставив значения в формулу (52), получаем

W_т= 1 ,75 * 9,54 = 16,7 см³/см

 

Эксцентрицитет приложения силы обжатия относительно центра тяжести приведенного сечения определяем по формуле, приведенной в п. 5.5

е₀ = =0,12 см.            (54)                                                                                                                                                                                                                                                                                                                                                  

Эксцентрицитет приложения равнодействующей растягивающей силы от внутреннего гидравлического давления определяем по формуле

В данном случае а = 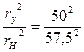=0,756;

 и ln  = ln 1,15 = 0,1397

г_n = r_у + h = 50+7,5 = 57,5 наружный радиус трубы, см, значения формулу (55), получаем

eon=3,.87-50=0,243см

Определение величины обжатия расчетного продольного сечения стенки трубы

Принимаем а₀ за величину предварительного напряжения в специальной напрягаемой арматуре по п.4.1:

 R_а^Н (56)

В данном случае R_а^Н = 17000 - нормативное сопротивление арматуры класса В-П, кгс/см² (табл. 20 СНиП П-21-75).

Подставив значения в формулу (56), получаем:

₀= 0,75 х 17000 = 12750 кгс/см².

Потери от релаксации напряжений в спиральной арматуре определяем по формуле

 (57)

Требуемое напряжение в спиральной арматуре с учетом половины потерь от релаксации стали составляет

`₀ =₀- 0,5 ₁ = 12750 - 0,5-1307 = 12097 кгс/см².     (58)                                                                                                                                                                                                                                                                               

Определим величину опрессовочного давления по формуле (3), приведенной в п. 4.2

`₀  = 0.9m_T,(59)

откуда

P_M =(59')

В данном случае:

р_п = 4 - величина потерь опрессовочного давления, кгс/см², принимаемая по п. 4.2;

m_T=1 - коэффициент точности натяжения спиральной армшуры, принимаемый по п. 4.2;

r_a - радиус окружности, по которой располагается центр тяжести спиралькой арматуры, определяемый по формуле

r_a = r_y + h-a = 50 + 7,5- 1,8 = 55,7 см. Подставив соответствующие значения в формулу (59¹) получим: