Экзаменационные билеты № 1-28 по математике (Определение предела функции по Гейне и по Коши, эквивалентность этих определений. Определение арктангенса и арккотангенса), страница 2

Билет 15

1. Предельный переход в неравенствах.

2. Определение и признак перпендикулярности двух плоскостей

3. Исследовать на периодичность и четность функции .

4. В правильной четырехугольной пирамиде EABCD точка M - середина BE. Построить линейный угол между плоскостями ADM и CDE.

Билет 16

1. Сумма бесконечно убывающей геометрической прогрессии. Обращение периодической десятичной дроби в обыкновенную.

2. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми, инвариантность определения угла.

3. При каждом значении параметра b указать, для каких значений x выполняется неравенство .

4. В правильной четырехугольной пирамиде EABCD точка M - середина BC. Построить линейный угол между плоскостями AEM и BED.

Билет 17

1. Теорема о сходимости монотонной ограниченной последовательности.

2. Теорема о существовании и единственности проходящей через данную точку прямой, параллельной данной прямой.

3. Решить неравенство         .

4. В правильной четырехугольной пирамиде EABCD построить линейный угол между плоскостями ABE и BEC.

.

Билет 18

1. Принцип двусторонней ограниченности для последовательностей.

2. Теорема о взаимоотношении двух параллельных прямых и плоскости.

3. Найти предел          

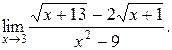
4. В правильной четырехугольной пирамиде EABCD точки M и N - середины AB и CE. Построить линейный угол между плоскостями DMN и ABCD.

Билет 19

1. Определение арксинуса и арккосинуса. Решение уравнений вида  sin и .

2. Теорема о трех параллельных прямых.

3. Найти предел         .

4. В правильной четырехугольной пирамиде EABCD точка M - середина BC. Построить линейный угол между плоскостями AEM и CDE.

.

Билет 20

1. Определение предела числовой последовательности. Теорема о единственности предела.

2. Определение и признак скрещивающихся прямых.

3. Найти корни уравнения  + ׀׀ = 1, принадлежащие интервалу (- π, π).

4. В правильной треугольной призме ABCDEF все ребра равны 1, точки M и N - середины AD и BE соответственно. Построить угол между плоскостями ANF и CME.

Билет 21

1. Формулы приведения. Тригонометрические функции половинного аргумента.

2. Теорема о скрещивающихся прямых

3. При каждом значении параметра b указать, для каких значений x выполняется неравенство .

4. В правильной треугольной призме ABCDEF точка M - середина AD. Построить угол между плоскостями CEM и ABED

Билет 22

1.  Логарифмы и их свойства. Логарифм произведения, степени, частного.

2. Взаимное расположение прямой и плоскости. Определение и признак параллельности прямой и плоскости

3. Исследовать на периодичность и четность функции .

4. В правильной треугольной призме ABCDEF точки M и N принадлежат AD и EF соответственно, причем AM=MD, EN:NF = 2. Построить угол между плоскостями CEM и ADN.

Билет 23

1. Логарифмическая функция, ее свойства и график.

2. Определение и признак параллельности двух плоскостей.

3. Найти предел         .

4. В правильной треугольной призме ABCDEF точка M - середина DE. Построить угол между плоскостями AMC и ABED.

Билет 24

1. Показательная функция, ее свойства и график.

2. Свойства параллельных плоскостей.

3. Найти предел .

4. В правильной треугольной призме ABCDEF точка M - середина DE. Построить угол между плоскостями AMC и DEC.

Билет 25

1. Определение, свойства, непрерывность и графики функций y = sin x и y= cos x.

2. Теоремы о взаимоотношении двух плоскостей и прямой.

3. Найти предел         .

4. В правильной треугольной призме ABCDEF все ребра равны 1. Построить линейный угол между плоскостями AEC и ABF.

Билет 26

1. Определение, свойства, непрерывность и графики функций y = tg x и y= ctg x.

2. Определение и признак перпендикулярности прямой и плоскости.

3. При каждом значении параметра b указать, для каких значений x выполняется неравенство .

4. В правильной треугольной призме ABCDEF все ребра равны 1. Построить линейный угол между плоскостями AEC и BEFC.

.

Билет 27

1. Тригонометрические функции cуммы и разности двух аргументов, тригонометрические функции двойного аргумента.

2. Прямая и обратная теоремы о двух параллельных прямых, перпендикулярных к плоскости.

3. Найти предел         .

4. В правильной четырехугольной пирамиде EABCD точки M и N на ребрах BE и DE, причем BM:ME = EN:ND = 2:1. Построить линейный угол между плоскостями AMN и CDE.

.

Билет 28

1. Определение арктангенса и арккотангенса. Решение уравнений вида  и с.

2. Теорема о трех перпендикулярах.

3. Найти предел         .

4. В правильной четырехугольной пирамиде EABCD точки M и N на ребрах BE и DE, причем BM:ME = EN:ND = 2:1. Построить линейный угол между плоскостями AMN и ABCD.