Определение средней численности работников на одно предприятие. Расчет дисперсии и среднего квадратического отклонения

Содержание

Задача 1. 3

Задача 2. 5

Задача 3. 6

Задача 4. 8

Задача 5. 10

Задача 6. 11

Задача 7. 13

Список литература. 15

Задача 1

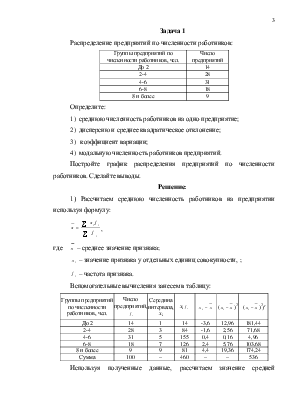
Распределение предприятий по численности работников:

Определите:

1)  среднюю численность работников на одно предприятие;

2)  дисперсию и среднее квадратическое отклонение;

3)   коэффициент вариации;

4)  модальную численность работников предприятий.

Постройте график распределения предприятий по численности работников. Сделайте выводы.

Решение:

1) Рассчитаем среднюю численность работников на предприятии используя формулу:

,

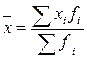где     – среднее значение признака;

 – значение признака у отдельных единиц совокупности, ;

 – частота признака.

Вспомогательные вычисления занесем в таблицу:

Используя полученные данные, рассчитаем значение средней численности работников на предприятии:

чел.

2) Определим показатели вариации – дисперсию и среднее квадратическое отклонение:

Дисперсия равна:

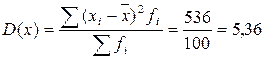чел.

Среднее квадратическое отклонение:

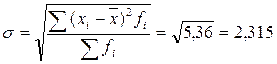чел.

3) Определим степень отклонения индивидуальных значений признака от среднего уровня:

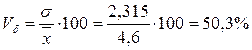
4) Значение моды определяем по формуле:

,

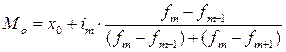где     – начало модального интервала (минимальное значение признака в модальном интервале);

 – величина соответственно модального интервала;

 – частота модального, до и послемодального интервалов соответственно.

Модальный интервал – интервал с наибольшей частотой признака, в нашей задаче это интервал от 4 до 6 чел. Подставляем исходные значения и получаем:

чел.

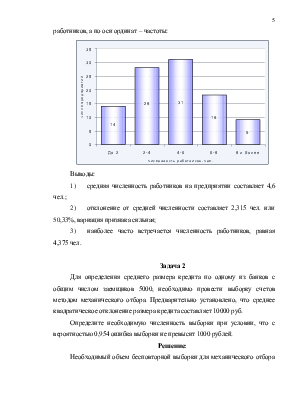
Построим гистограмму распределения численности работников по предприятиям, для этого по оси абсцисс отложим значения численности работников, а по оси ординат – частоты:

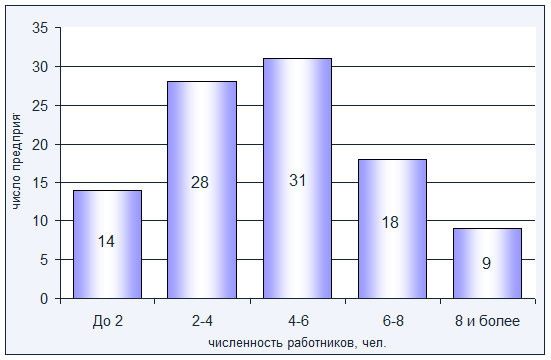
Выводы:

1)  средняя численность работников на предприятии составляет 4,6 чел.;

2)  отклонение от средней численности составляет 2,315 чел. или 50,33%, вариация признака сильная;

3)  наиболее часто встречается численность работников, равная 4,375 чел.

Задача 2

Для определения среднего размера кредита по одному из банков с общим числом заемщиков 5000, необходимо провести выборку счетов методом механического отбора. Предварительно установлено, что среднее квадратическое отклонение размера кредита составляет 10000 руб.

Определите необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит 1000 рублей.

Решение:

Необходимый объем бесповторной выборки для механического отбора можно определить при помощи формулы:

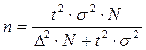, где    Δ – предельная ошибка выборки;

σ² – выборочная дисперсия;

t – коэффициент доверия, который вычисляется при помощи таблицы;

N– объем генеральной совокупности;

n – численность выборки.

Коэффициент доверия при вероятности Р = 0,954 составляет t = 2.

Подставив исходные данные получим:

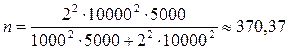
Вывод: для того, чтобы ошибка выборки при проведении исследования не превысила 1000 руб. с вероятностью 0,954, необходимо исследовать не менее 371 заемщика.

Задача 3

Ежегодные темпы прироста реализации товара «А» составили в % к предыдущему году: 1998 – 5,5; 1999 – 6,2; 2000 – 8,4; 2001 – 10,5; 2002 – 9,2.

Исчислите за приведенные годы базисные темпы динамики по отношению к 1997 году и среднегодовой темп прироста за 1998-2002 гг.

Решение:

Вычислим коэффициенты цепные коэффициенты роста для каждого года:

,

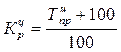где     – цепной темп прироста.

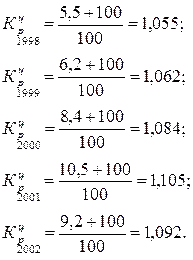
Далее вычислим базисные коэффициенты роста, используя связь цепных и базисных показателей:

Соответственно темпы роста и прироста составят:

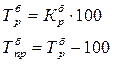
Занесем показатели в таблицу:

Определим среднегодовой темп роста:

Среднегодовой темп прироста:

Задача 4

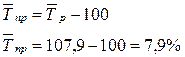
Имеются данные о спросе на книжную продукцию и структуре оборота книжного издательства в отчетном году:

Определите уровень согласованности между спросом на книжную продукцию и структурой оборота издательства с помощью коэффициентов корреляции Спирмена и Фехнера.

Решение:

Коэффициент ранговой корреляции Спирмена рассчитывается следующим образом:

,

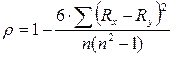где    R_x – ранг признака Х;

R_y – ранг признака У;

n– число наблюдений.

Составим вспомогательную таблицу:

Подставляя полученные значения в формулу, получаем:

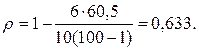
Коэффициент корреляции рангов Фехнера равен:

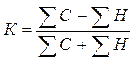, где    С – ситуация совпадений знаков отклонений от среднего ранга;

Н – ситуация несовпадений знаков отклонений от среднего ранга.

Средний ранг равен: .

Составим вспомогательную таблицу для расчета коэффициента Фехнера:

Итак,

Рассчитанные коэффициенты позволяют говорить о слабой зависимости