Передача электрической энергии вдоль проводов, преобразование электроэнергии одного напряжения в электроэнергию другого напряжения, а также преобразование электрической энергии в механическую совершается посредством электромагнитного поля. Перечисленные процессы связаны с изменениями и колебаниями электромагнитной энергии. Колебания электромагнитной энергии происходят между элементами электрической системы, в том числе между источником энергии и приемником: в некоторые моменты времени энергия поступает не от источника к приемнику, а наоборот, от приемника к источнику. Однако энергия, поступающая от источника за период, превосходит энергию, возвращаемую ему остальными элементами электрической сети. Среднее значение мощности, отдаваемое однофазному приемнику, равно:
Р = U I cosj.
Это значение носит название активной мощности.
Активной мощности соответствует активный ток Ia, который является только составляющей полного тока I. Все элементы электрической сети должны быть рассчитаны на прохождение полного тока. Поэтому трансформаторы, генераторы и двигатели характеризуются величиной UI, называемой условно полной мощностью.
Вторая составляющая полной мощности ‑ UIsinj носит название реактивной мощности. Это название чисто условно, так как реактивная мощность не создает работы. Реактивная мощность характеризует колебания электромагнитной энергии. Для простейшей цепи из R, L и С реактивная мощность равна скорости поступления энергии в магнитное и электрическое поле. Все элементы электрической сети должны рассчитываться на прохождение не только активной, но и реактивной мощности. Приемники электрической энергии, работе которых сопутствуют электромагнитные поля, следует рассматривать как потребителей активной и реактивной мощности одновременно.
Линии и трансформаторы также связаны с электромагнитным полем, поэтому должны рассматриваться как потребители реактивной мощности.
Значения реактивной мощности, необходимые для линий и трансформаторов, рассматриваются как потери реактивной мощности.
Если за 100% принять всю реактивную мощность, циркулирующую в системе, то эта мощность распределяется следующим образом:
асинхронные двигатели 65 – 75%
трансформаторы 15 – 30%
воздушные линии 5 – 10%.
Таким образом, потребителям должны доставляться активная и реактивная мощности. Одновременно необходимо покрывать потери активной и реактивной мощности (последние условно) в элементах электрической сети.
Реактивная мощность доставляется от генераторов или от компенсаторов.
Рассмотрим возможные варианты снабжения реактивной мощностью, анализируя при помощи векторных диаграмм изменение коэффициента мощности.
1. Генератор работает на нагрузку, имеющую индуктивный характер; компенсаторы отсутствуют (рис. 4.8).
Из векторной диаграммы видно, что коэффициент мощности в начале электропередачи cosj, меньше, чем у потребителя cosj2, за счет преобладания в электропередаче реактивных потерь мощности над потерями активной мощности.
2. Потребитель часть реактивной мощности получает от компенсатора (рис. 4.9).
3. Потребитель полностью получает реактивную мощность от компенсатора (рис. 4.10).
4. Компенсатор выдает реактивную мощность потребителю и покрывает потери реактивной мощности (рис. 4.11).
5. Компенсатор выдает реактивную мощность потребителю, электропередаче и генератору (рис. 4.12).
Из векторных диаграмм видно, что чем меньше вырабатывает генератор реактивной мощности, тем больше повышается его коэффициент мощности, а при потреблении реактивной мощности генератором его cosj становится опережающим.
Для обозначения полной мощности в символическом методе имеются два различных выражения, отличающиеся для одного и того же вида нагрузки только знаком у реактивной мощности.
В первом обозначении полная мощность при индуктивной нагрузке будет:
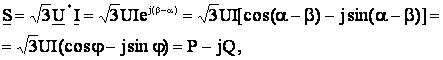(4.64)
где обозначения даны на рис. 4.13. Аналогично при емкостной нагрузке:
.
При втором обозначении для случая индуктивной нагрузки получим:
(4.65)
и для случая емкостной:
S = P – jQ.
Полагая вектор напряжения совпадающим с положительным направлением действительной оси, для тока в случае индуктивной нагрузки можем написать
и при опережающем токе
Сравнивая выражения мощности и тока, можно заметить однотипность формул полного тока и полной мощности при первом ее обозначении, т.е.
В этом состоит преимущество такого обозначения. Однако, далее будем пользоваться обозначением (4.65), так как ему соответствует большая часть программ на ЭВМ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.