Учёт согласованности и непротиворечивости для структурированных критериев. Учёт фактора времени в оценочных функциях. Дисконт ирование. Функции эффекта и затрат. Распределение эффекта по сроку эксплуатации. Примеры детерминированных и рандомизированных критериев. Виды экономических критериев. Размерные и безразмерные технические показатели. Социальные и эстетические требования. Виды свёрток оценочных функций качественных характеристик.
Взаимодействие математической модели и алгоритма оптимизации. Классификация методов оптимизации. Логическая схема алгоритма оптимизации. Алгоритм приведения любой задачи ЛП к канонической форме. Идея симплекс-метода. Базис задачи и опорный вектор системы линейно независимых векторов. Пример решения задачи ЛП симплекс-методом. Графическая интерпретация решения задачи ЛП.
Блок-схема сеточного алгоритма полного перебора значений аргуменгтов. Пример поиска экстремума функции сеточным алгоритмом. Градиентный алгоритм оптимизации. Пример минимизации нелинейной функции градиентным методом. Траектория поиска градиентным методом. Сущность релаксационного алгоритма. Релаксационный алгоритм Хука-Дживса. Блок-схема алгоритма Хука-Дживса. Траектория поиска методом Хука-Дживса. Блок-схема алгоритма случайного поиска. Формула шага оптимизации для непрерывных компонент вектора Х. Траектория поиска экстремума функции алгоритмом случайного поиска.
Необходимое условие адекватности проектируемой системы и её моделью. Соотношение между сложностью модели и её адекватностью. Интервал гносеологической точности.. Нормируемая степень адекватности математической модели. Взаимозависимость проектных запасов. Достаточность степени адекватности модели синтеза. Связь достаточной адекватности с исследованием чувствительности решения при изменении правых частей ограничений и параметров исходных данных. Алгоритм оценки адекватности модели. Оценка адекватности и инженерный анализ результатов проектирования.
Цель изучения окрестности оптимальной точки пространства состояний проектируемой системы. Замена целевой функции линейным приближением. Определение зависимости компонентов оптимального решения от значений элементов технического задания. Построение зависимости критерия от компонентов вектора оптимизируемых переменных. Коэффициенты эластичности решения и зона безразличия при решении задачи синтеза.
Задачи
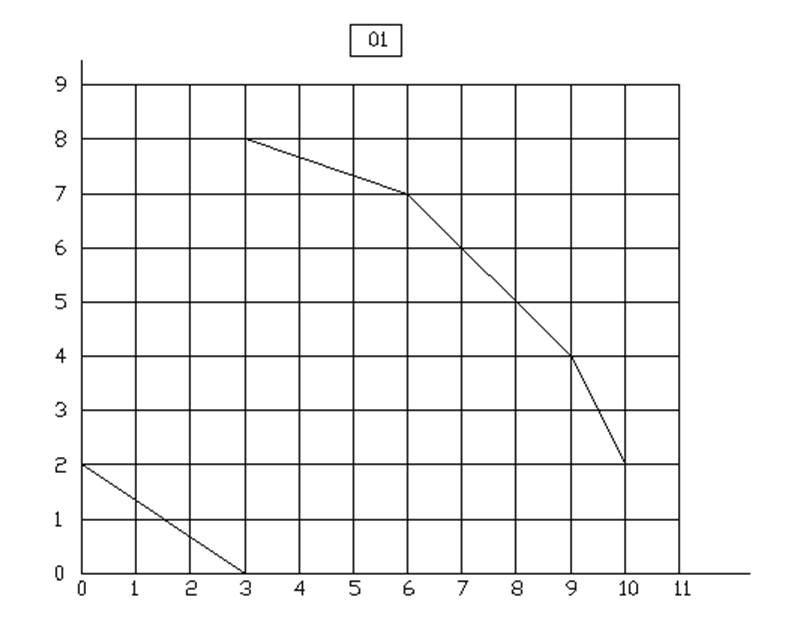
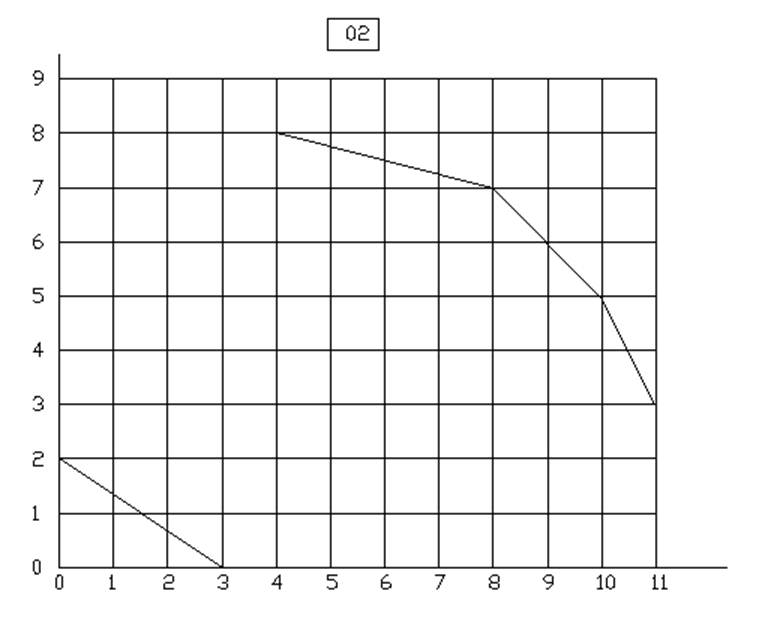
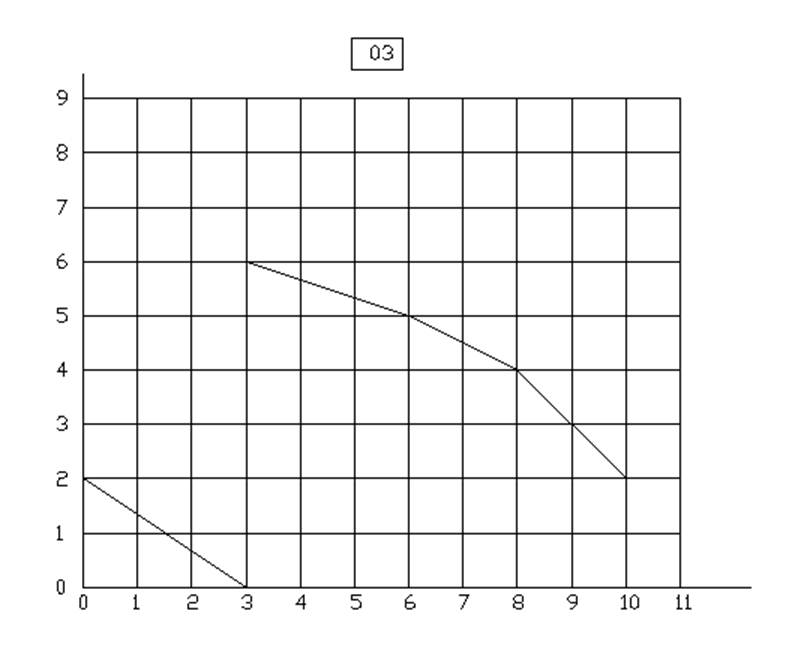
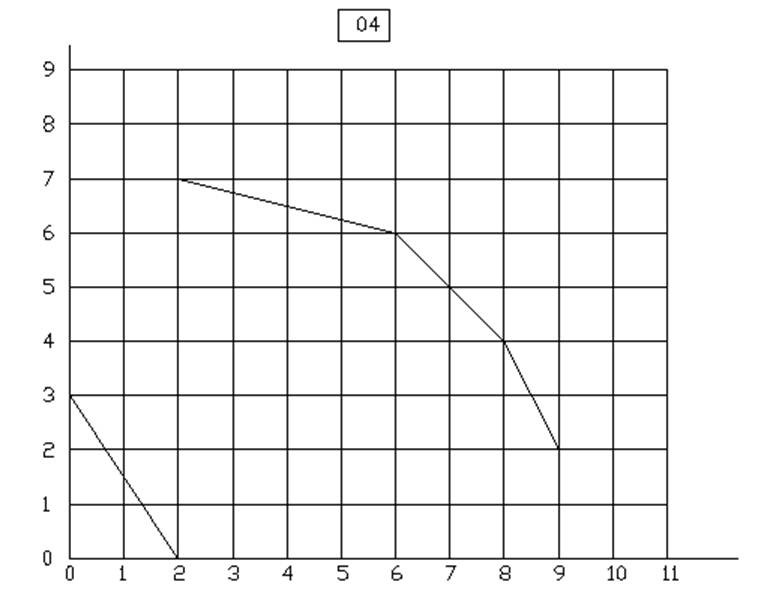
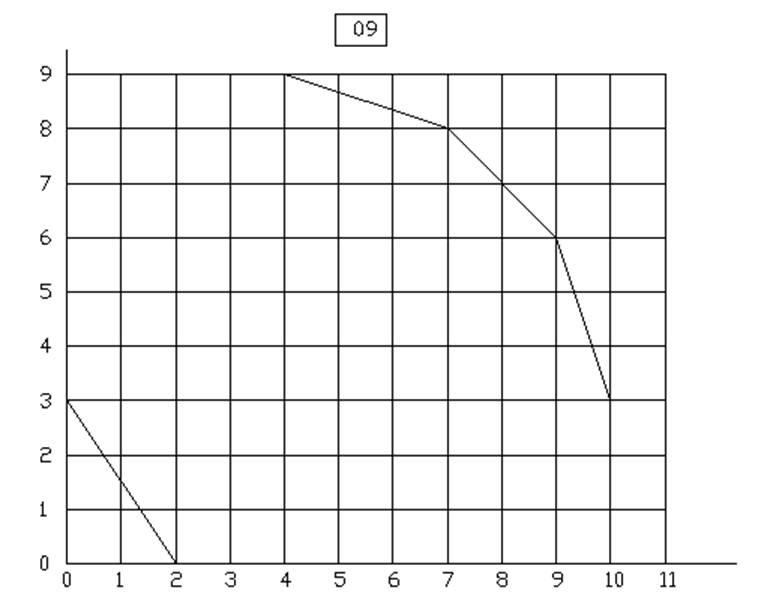
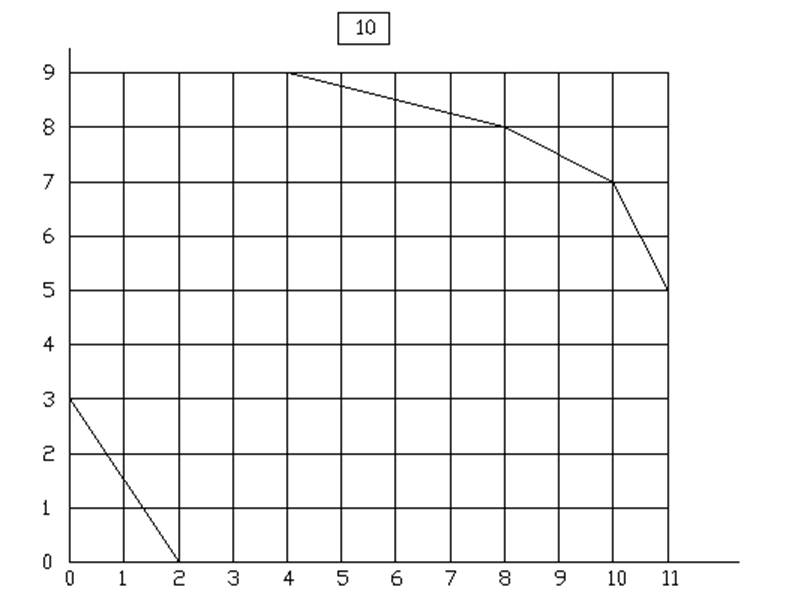
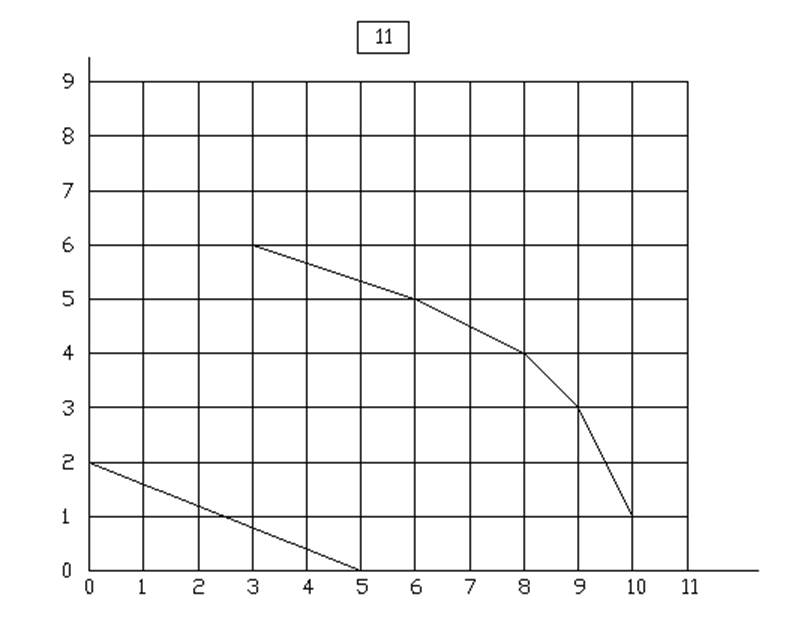
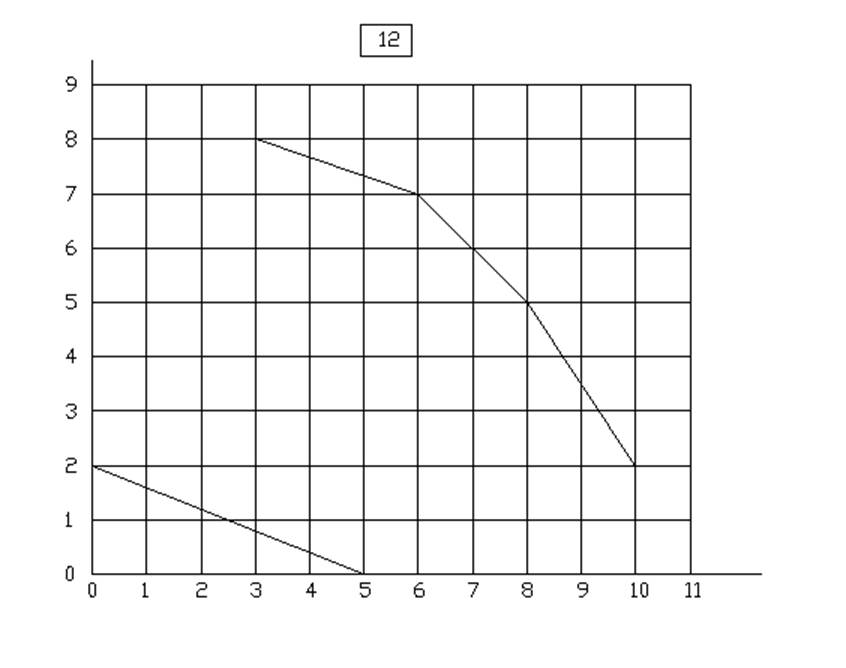
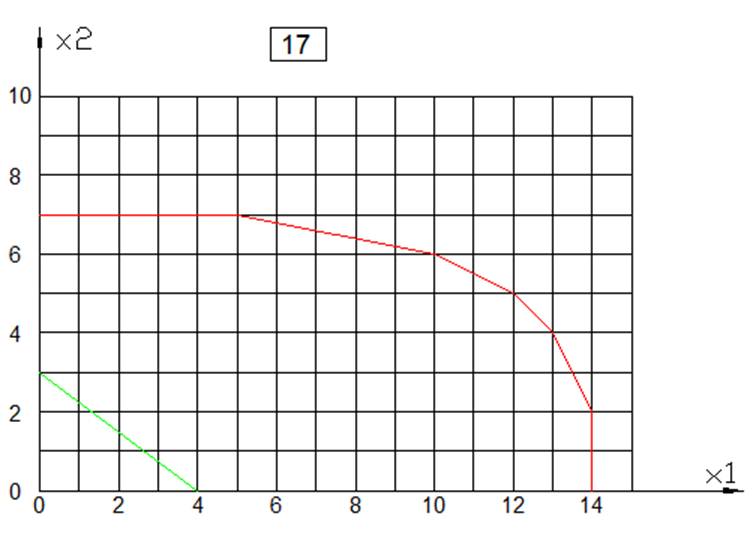
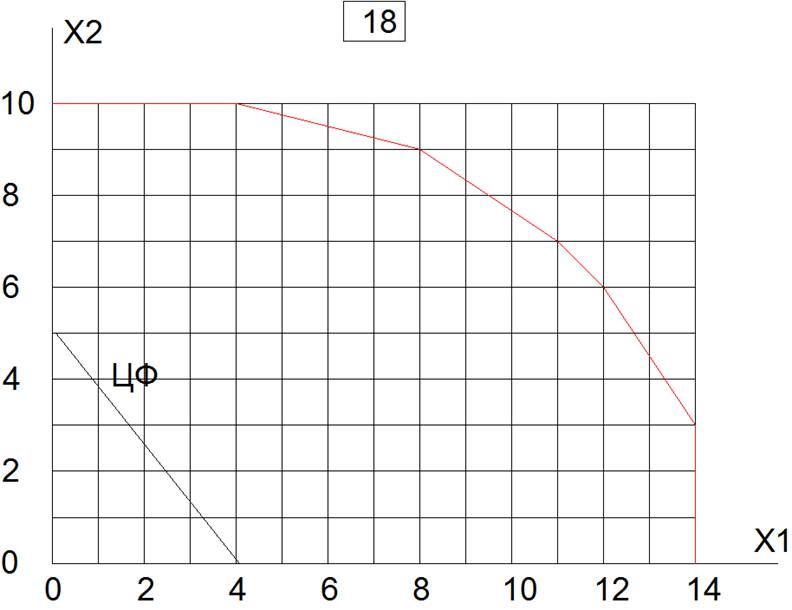
10.
1.1 2X14 + X24 -( X1 + X2)2 à max(min), X έ R2
20.2 2X14 + 2X24 -( X1 + X2)2 à max(min), X έ R2
20.3 2X14 + X24 -( 2X1 + X2)2 à max(min), X έ R2
20.4 2X14 + X24 -( X1 + 2X2)2 à max(min), X έ R2
20.5 X14 + 2X24 -( X1 + X2)2 à max(min), X έ R2
20.6 X14 + X24 -( 2X1 + X2)2 à max(min), X έ R2
20.7 X14 + X24 -( X1 + 2X2)2 à max(min), X έ R2
20.8 X14 + 3X24 -( X1 + X2)2 à max(min), X έ R2
20.9 X14 + 3X24 -( 2X1 + X2)2 à max(min), X έ R2
20.10 X14 + 3X24 -( X1 + 2X2)2 à max(min), X έ R2
20.11 X14 + 3X24 -( 3X1 + X2)2 à max(min), X έ R2
20.12 2X14 + 3X24 -( X1 + X2)2 à max(min), X έ R2
20.13 2X14 + 3X24 -( 2X1 + X2)2 à max(min), X έ R2
20.14 2X14 + 3X24 -( X1 + 2X2)2 à max(min), X έ R2
20.15 2X14 + 4X24 -(2 X1 + X2)2 à max(min), X έ R2
20.16 2X14 + 4X24 -( X1 +2 X2)2 à max(min), X έ R2
20.17 X14 + 4X24 -( X1 + X2)2 à max(min), X έ R2
20.18 X14 + 4X24 -( 2X1 + X2)2 à max(min), X έ R2
20.19 2X14 + 4X24 -( 2X1 + X2)2 à max(min), X έ R2
23. Решить задачу методом множителей Лагранжа.
23.1 f(x) = x12 + 2x22 + x32 ->min при 2x1 - x2 + x3 ≤ 6 x1 + x2 + x3 = 4
23.2 f(x) = x12 + x22 + 2x32->min при 2x1 - 2x2 + x3 ≤ 7 x1 + x2 + x3 = 4
23.3 f(x) = 2x12 + x22 + x32->min при 2x1 - x2 +2 x3 ≤ 5 x1 + x2 + x3 = 5
23.4 f(x) = 3x12 + x22 + x32 ->min при 3x1 - 3x2 + x3 ≤ 7 2x1 + x2 + x3 = 6
23.5 f(x) = x12 + 4x22 + x32 ->min при 3x1 - x2 + 3x3 ≤ 6 x1 + 2x2 + x3 = 4
23.6 f(x) = x12 + x22 + 5x32 ->min при 3x1 - 4x2 + x3 ≤ 4 x1 + x2 + 2x3 = 6
23.7 f(x) = 2x12 + x22 + x32 ->min при 2x1 - 3x2 + 4x3 ≤ 6 3x1 + x2 + x3 = 5
23.8 f(x) = x12 + 2x22 + x32 ->min при 3x1 - x2 + 3x3 ≤ 7 x1 + 3x2 + x3 = 4
23.9 f(x) = x12 + x22 + 2x32 ->min при 4x1 - 2x2 + x3 ≤ 6 x1 + x2 + 3x3 = 6
23.10 f(x) = 3x12 + x22 + x32 ->min при 5x1 - x2 + 2x3 ≤ 4 4x1 + x2 + x3 = 5
23.11 f(x) = x12 + 3x22 + x32 ->min при 2x1 - 3x2 + x3 ≤ 7 x1 + 4x2 + x3 = 4
23.12 f(x) = x12 + x22 + 3x32 ->min при 3x1 - x2 + 3x3 ≤ 6 x1 + x2 + 4x3 = 6
23.13 f(x) = 4x12 +x22 + x32 ->min при 4x1 - 4x2 + 2x3 ≤ 4 5x1 + x2 + x3 = 5
23.14 f(x) = x12 + 4x22 + x32 ->min при 5x1 - 2x2 + x3 ≤ 7 x1 + 5x2 + x3 = 4
23.15 f(x) = x12 + x22 + 4x32 ->min при 2x1 - x2 + 2x3 ≤ 6 x1 + x2 + 5x3 = 6
23.16 f(x) = 5x12 + x22 + x32 ->min при 3x1 - 2x2 + x3 ≤ 4 6x1 + x2 + x3 = 5
23.17 f(x) = x12 + 5x22 + x32 ->min при 4x1 - x2 + 3x3 ≤ 7 x1 + 6x2 + x3 = 4
23.18 f(x) = x12 + x22 + 5x32 ->min при 5x1 - 3x2 + x3 ≤ 6 x1 + x2 + 6x3 = 6
23.19 f(x) = 6x12 + x22 + x32 ->min при 2x1 - x2 + 4x3 ≤ 4 7x1 + x2 + x3 = 5
24. Решить следующую задачу методом множителей Лагранжа.
24.1 f(x) = 2x12 + x22 ->max(min) при x14 - x24 = 1
24.2 f(x) = x12 + 2x22 ->max(min) при 2x14 - x24 = 1
24.3 f(x) = 3x12 + x22 ->max(min) при x14 - 2x24 = 1
24.4 f(x) = x12 + 3x22 ->max(min) при 3x14 - x24 = 1
24.5 f(x) = 4x12 + x22 ->max(min) при x14 - 3x24 = 1
24.6 f(x) = x12 + 4x22 ->max(min) при x14 - x24 = 1
24.7 f(x) = 2x12 + x22 ->max(min) при 2x14 - x24 = 1
24.8 f(x) = x12 + 2x22 ->max(min) при x14 - 2x24 = 1
24.9 f(x) = 3x12 + x22 ->max(min) при 3x14 - x24 = 1
24.10 f(x) = x12 + 3x22 ->max(min) при x14 - 3x24 = 1
24.11 f(x) = 4x12 + x22 ->max(min) при x14 - x24 = 1
24.12 f(x) = x12 + 4x22 ->max(min) при 2x14 - x24 = 1
24.13 f(x) = 5x12 + x22 ->max(min) при x14 - 2x24 = 1
24.14 f(x) = x12 + 5x22 ->max(min) при 3x14 - x24 = 1
24.15 f(x) = 2x12 + x22 ->max(min) при x14 - 3x24 = 1
24.16 f(x) = x12 + 2x22 ->max(min) при x14 - x24 = 1
24.17 f(x) = 3x12 + x22 ->max(min) при 2x14 - x24 = 1
24.18 f(x) = x12 + 3x22 ->max(min) при x14 - 2x24 = 1
24.19 f(x) = 4x12 + x22 ->max(min) при 3x14 - x24 = 1
МЕТОД ВЕТВЕЙ И ГРАНИЦ
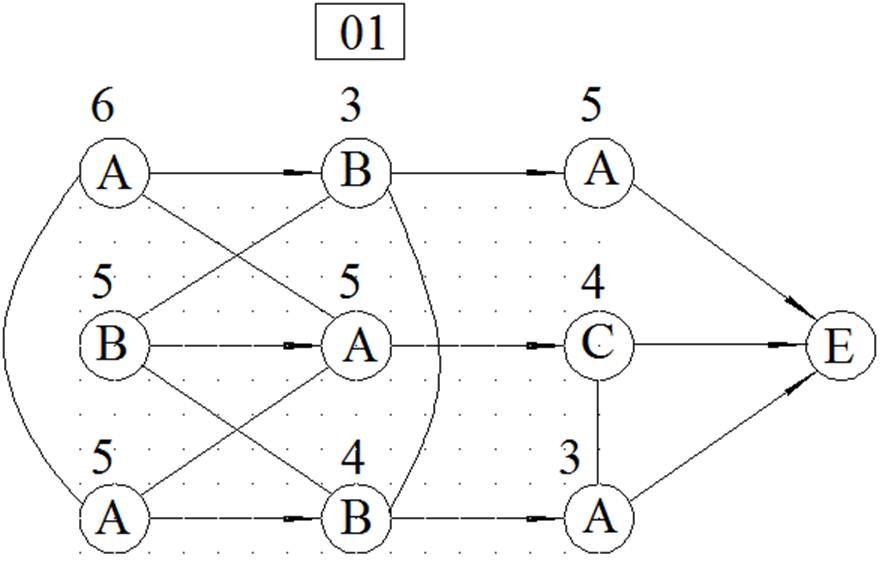
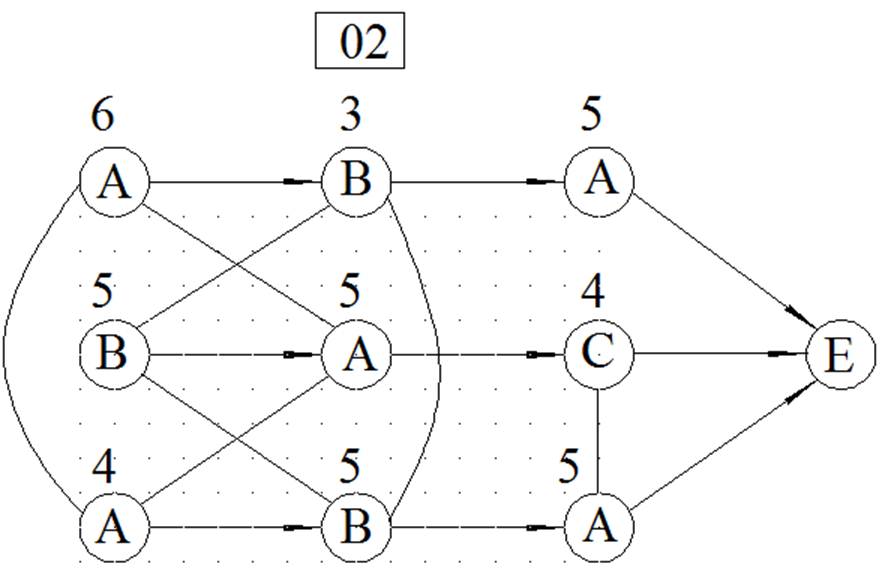
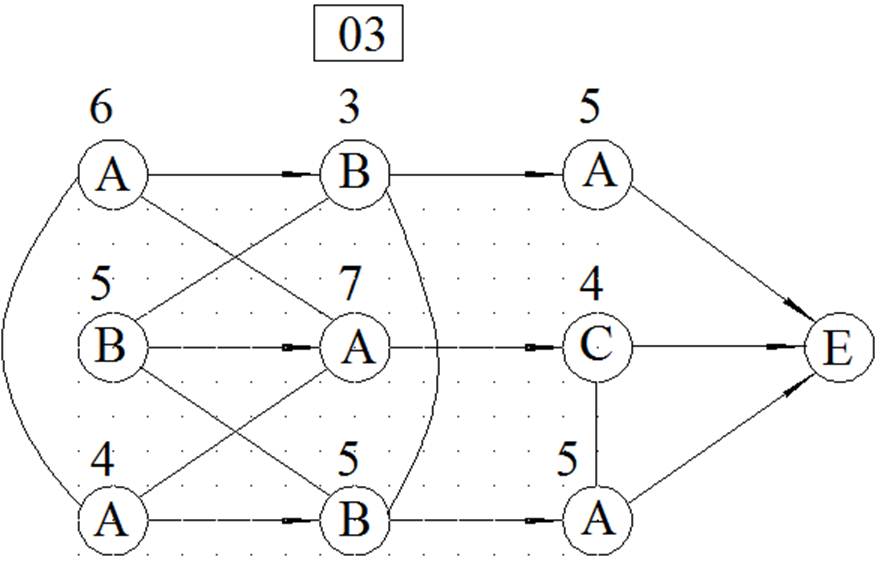
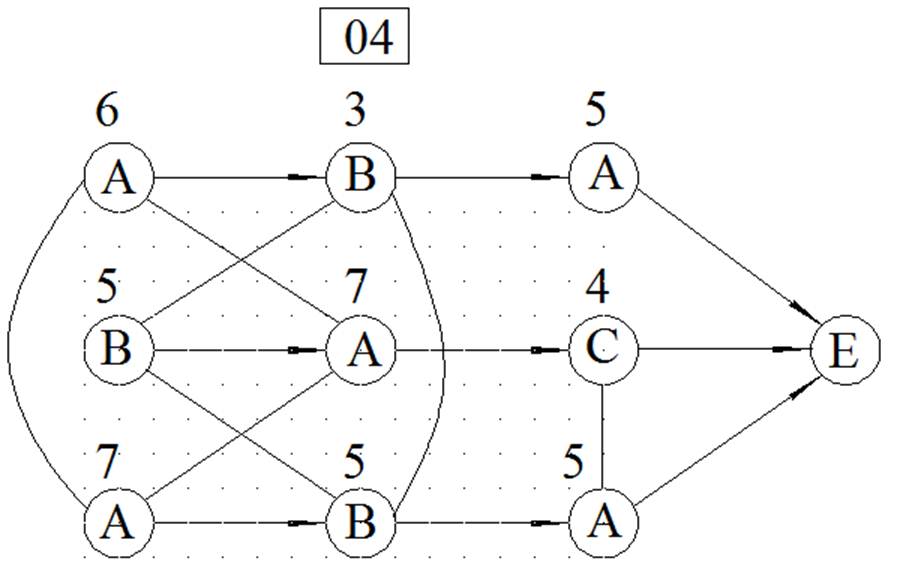
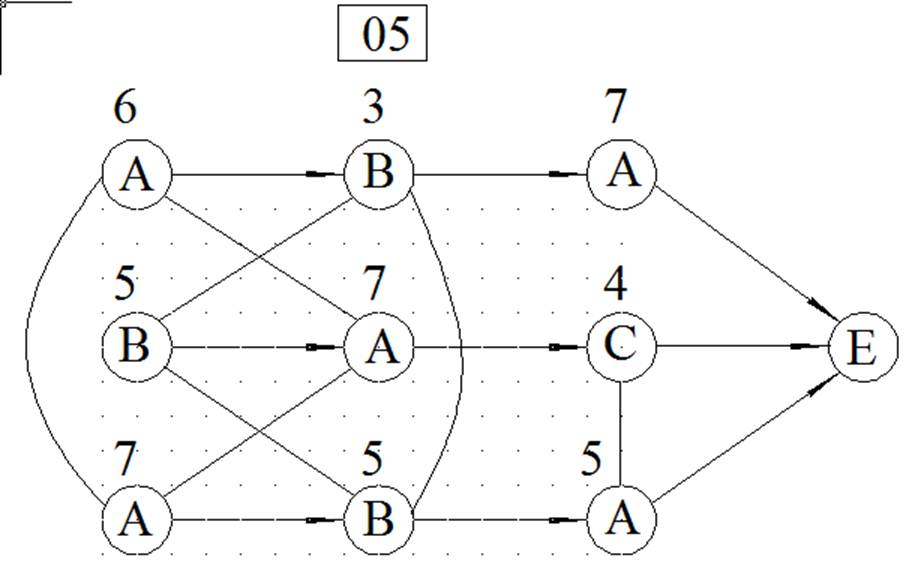
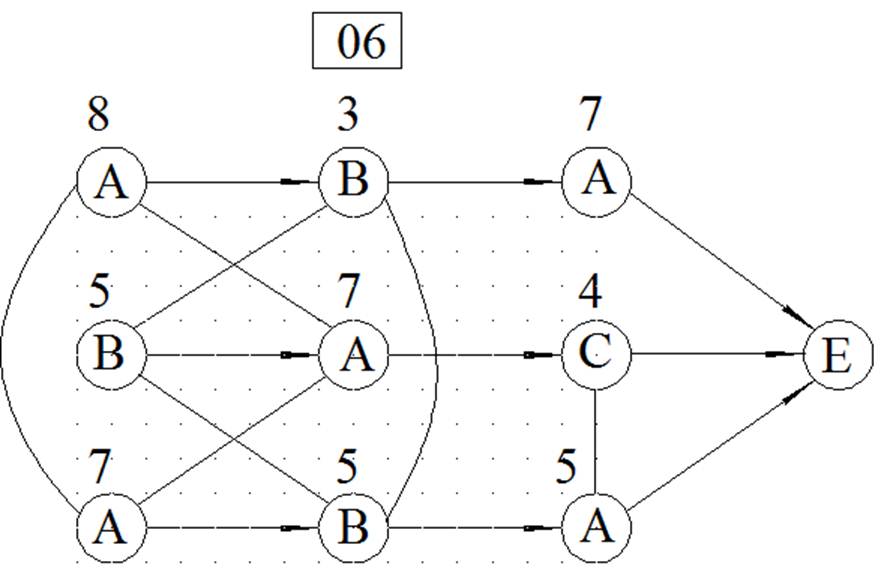
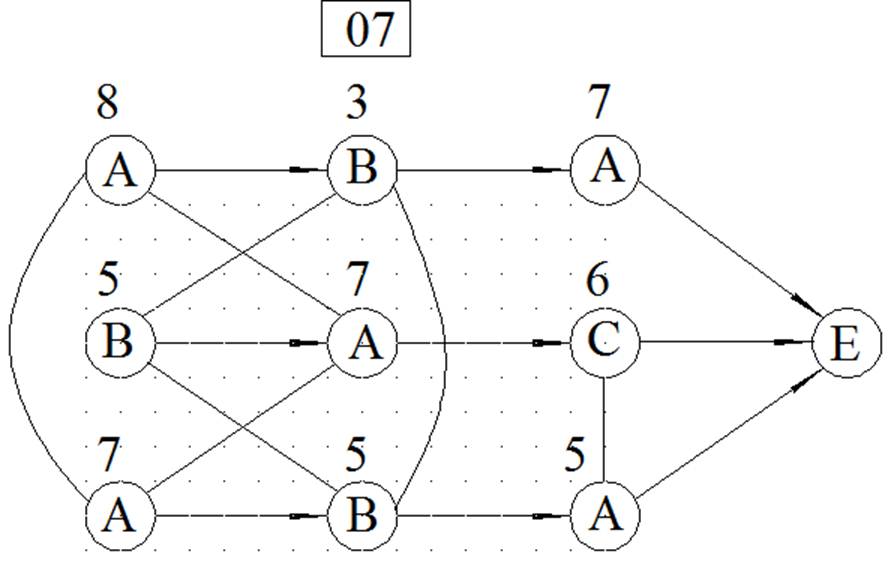
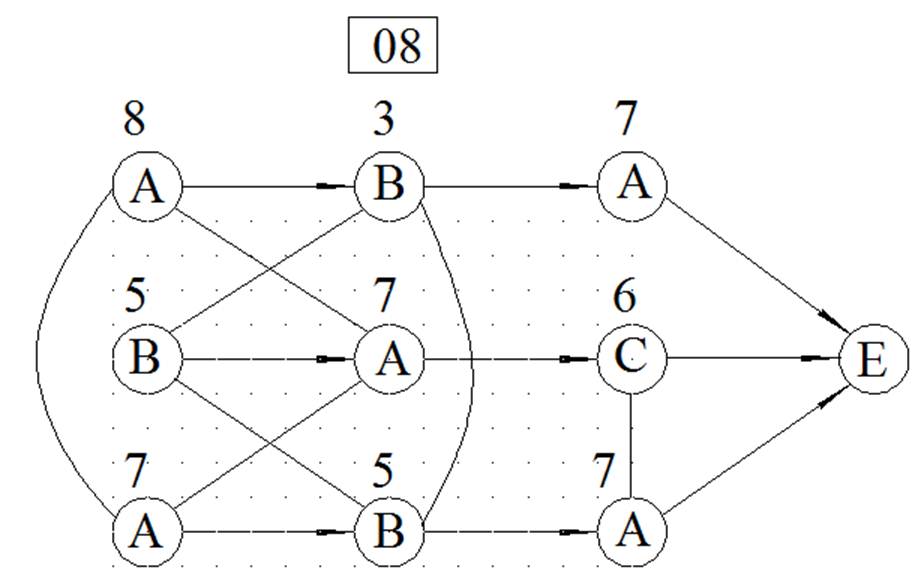
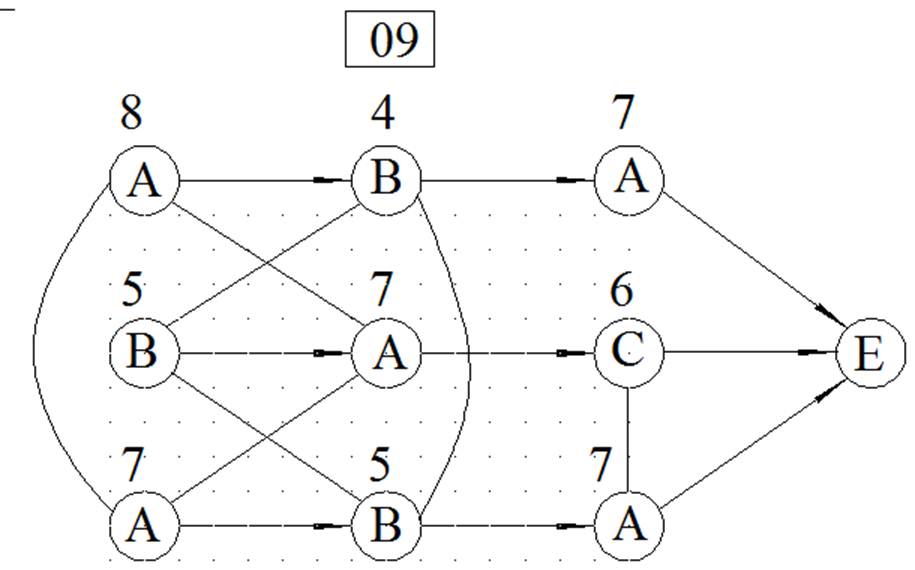
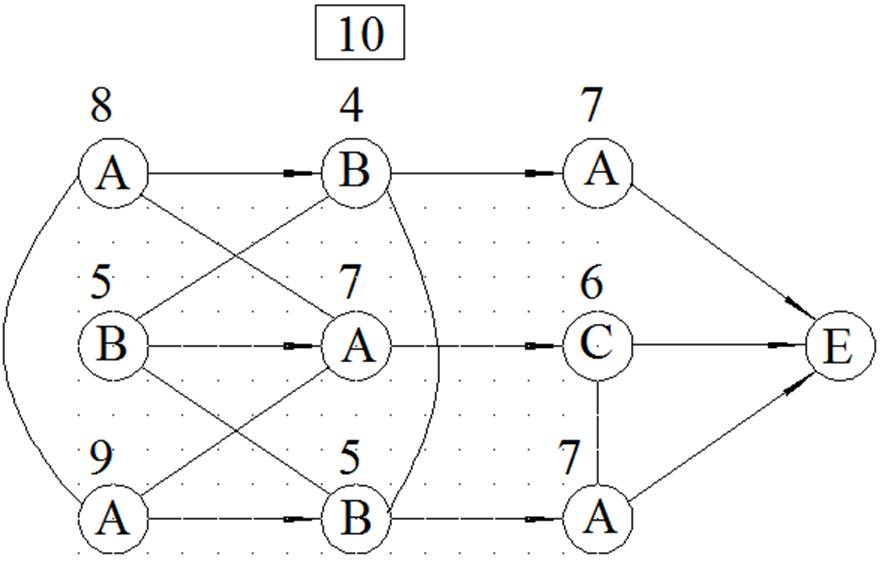
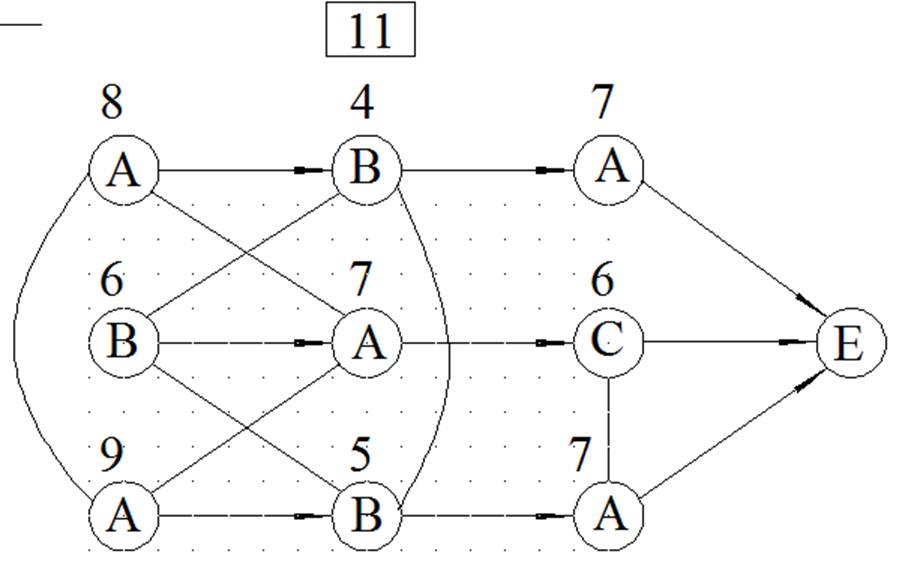
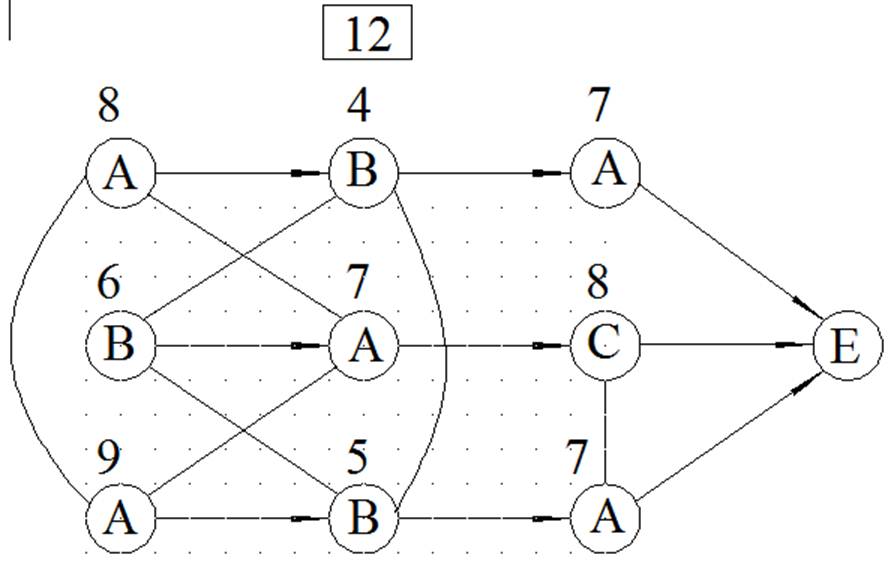
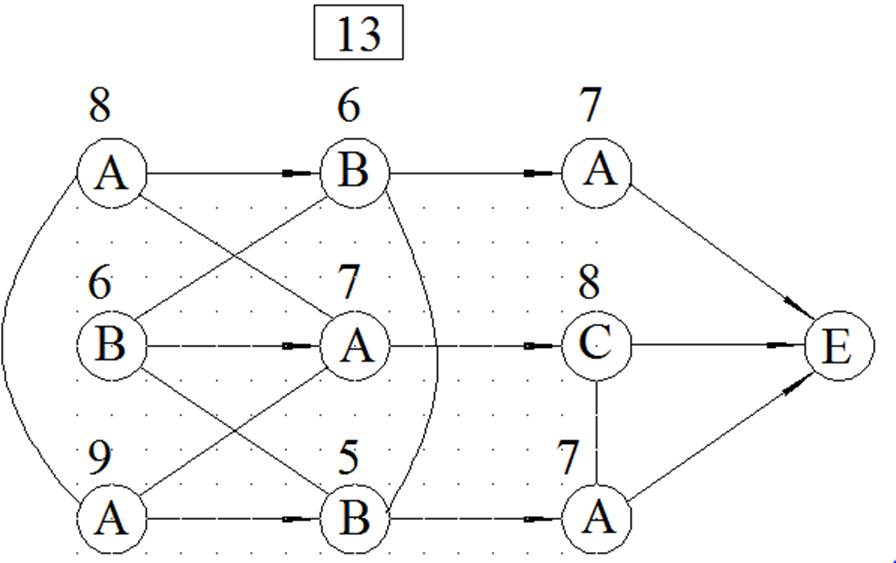
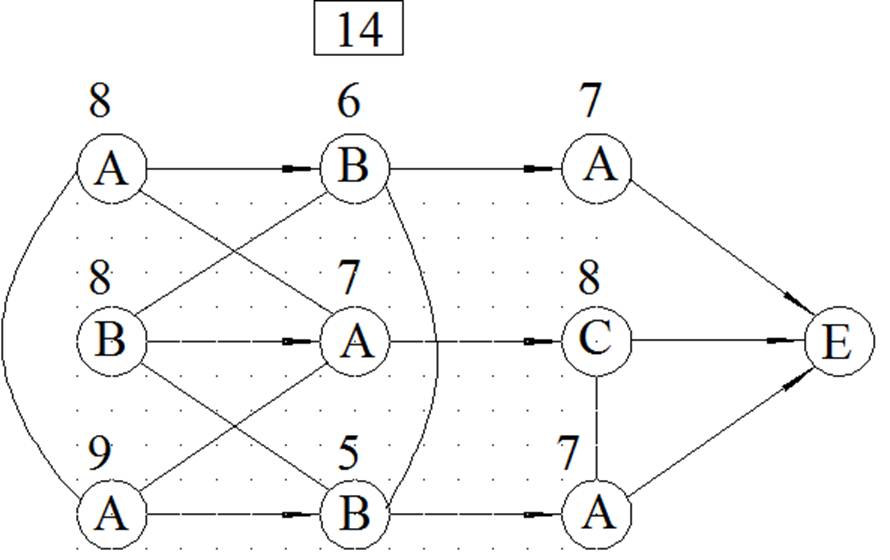
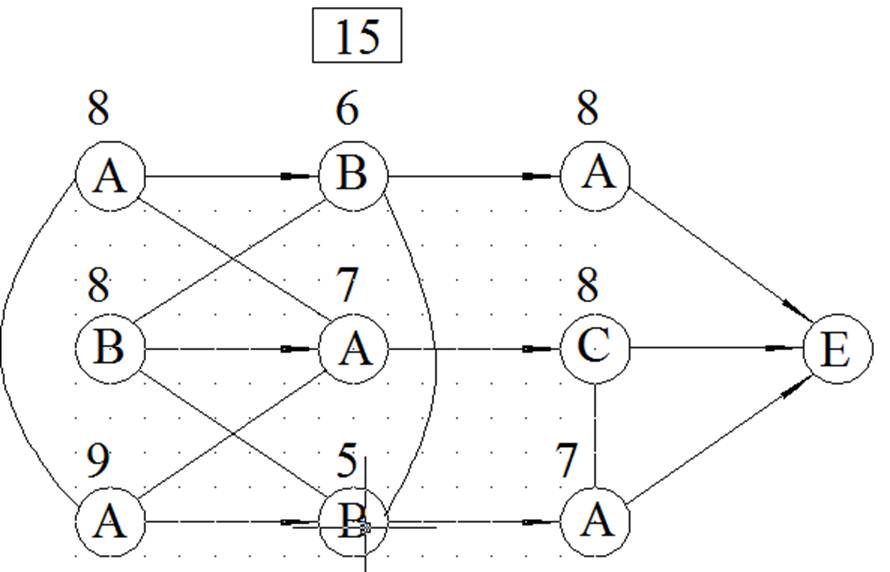
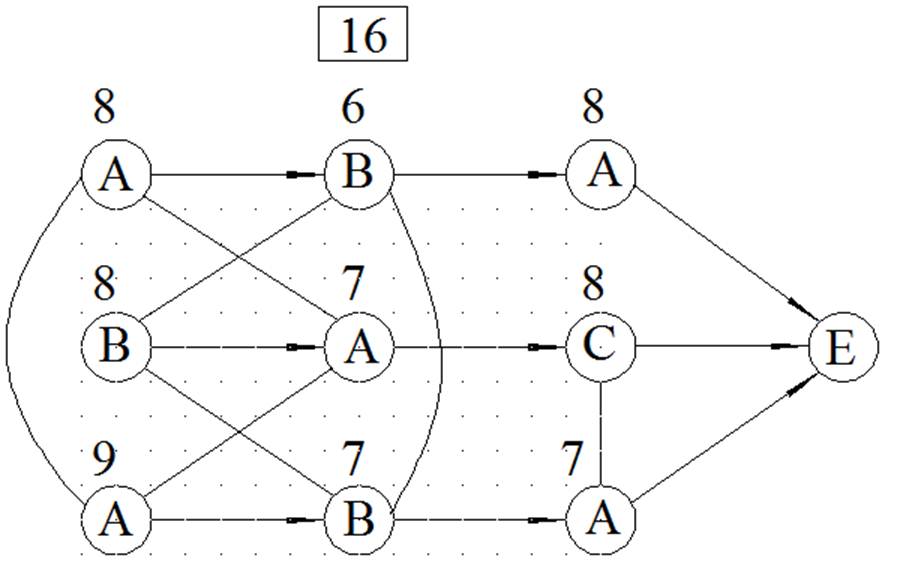
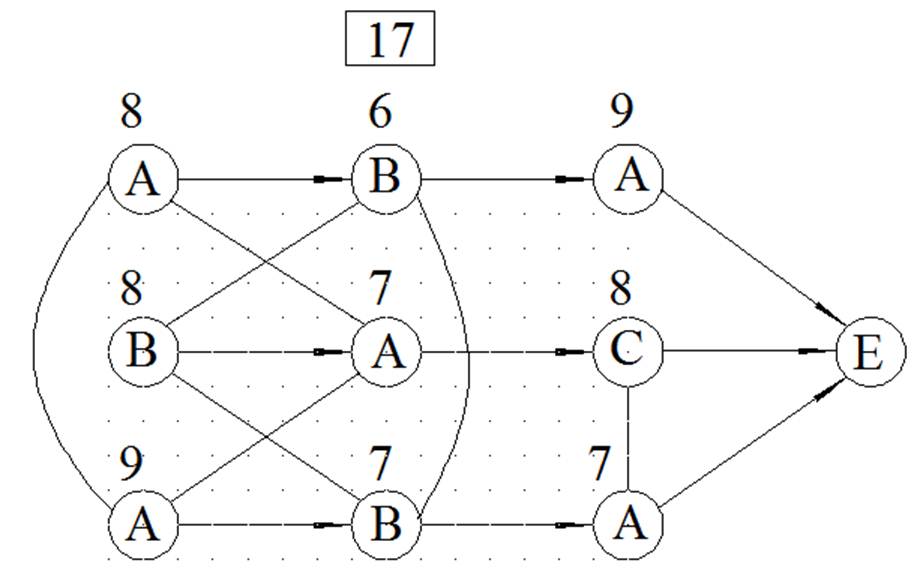
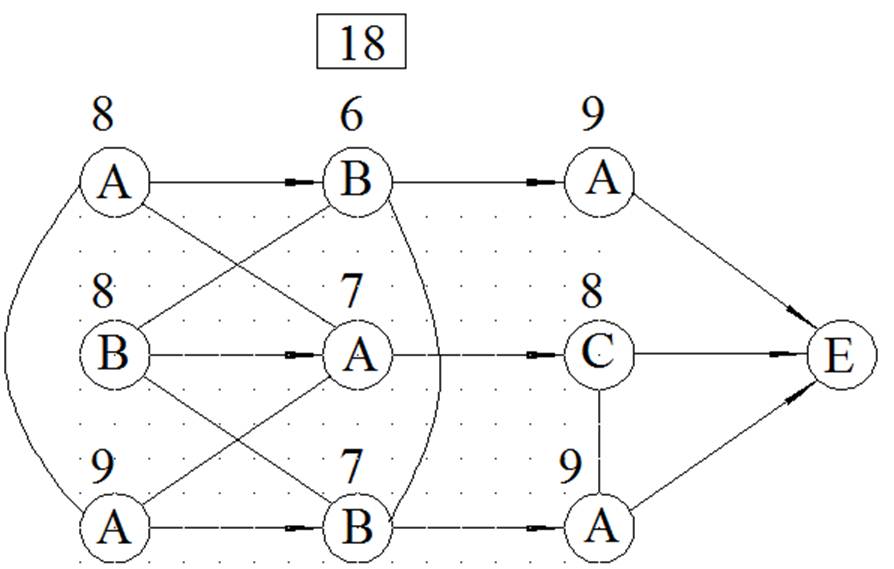
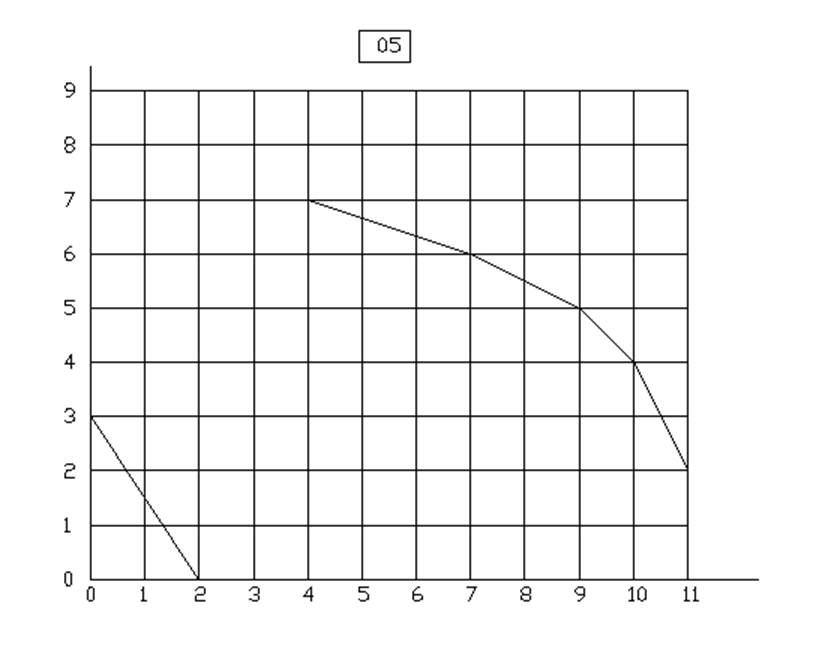
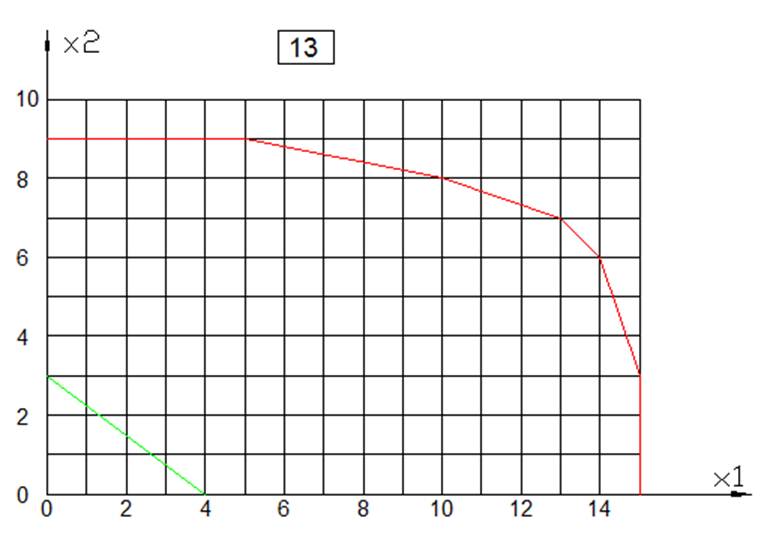
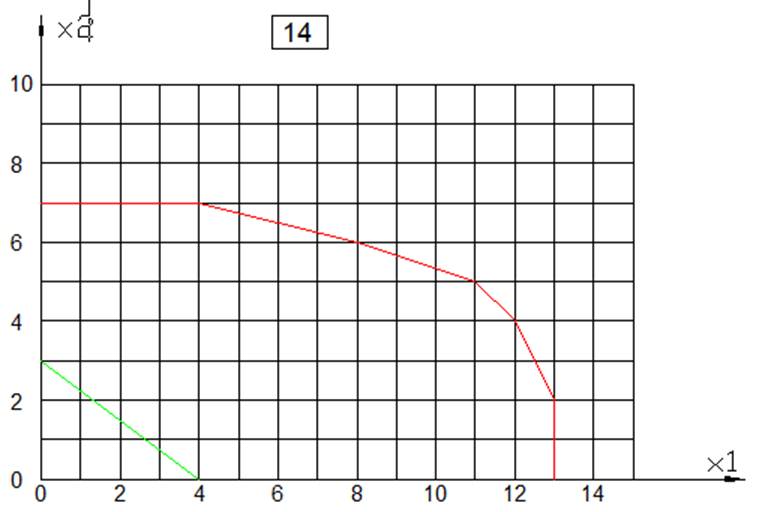
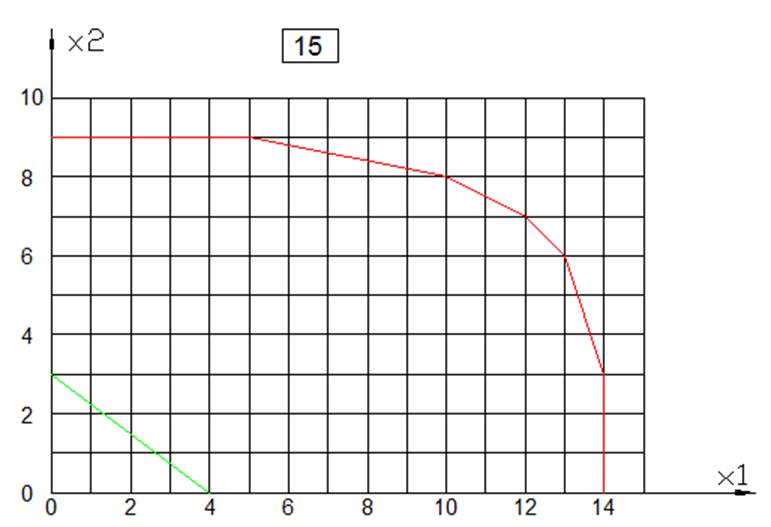
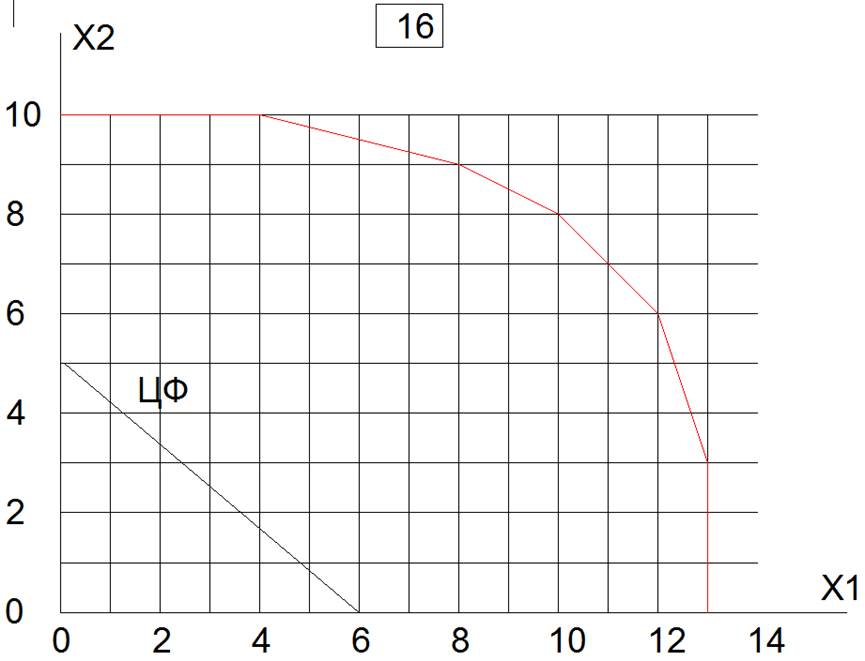
ЦЕЛОЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ
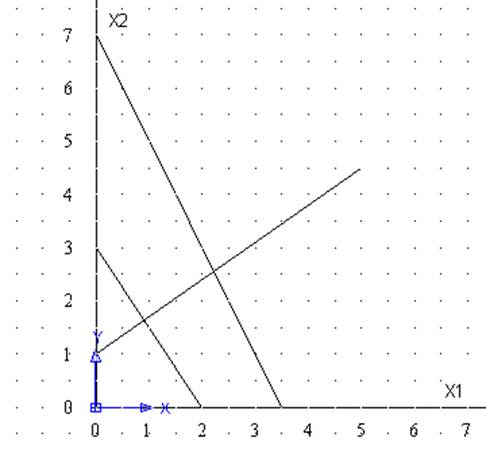
Вариант 1 у=3Х1+2Х2
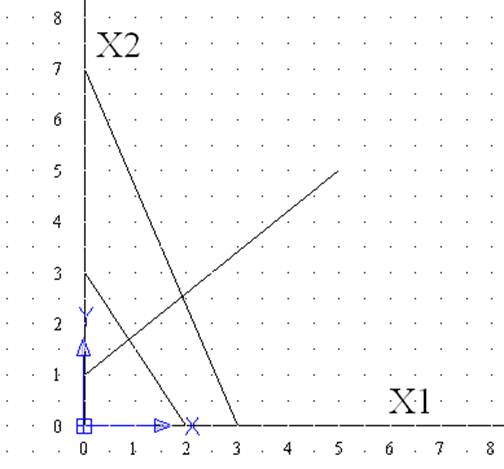
Вариант 2 у=3Х1+2Х2
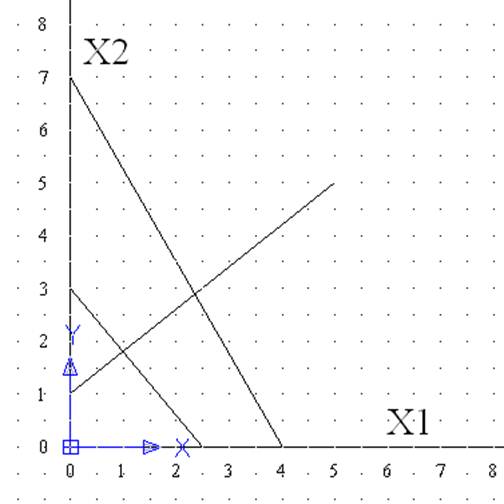
Вариант 3 у=3Х1+2.5Х2
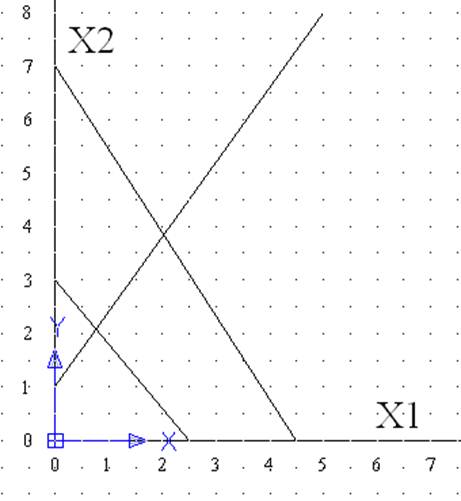
Вариант 4 у=3Х1+2.5Х2
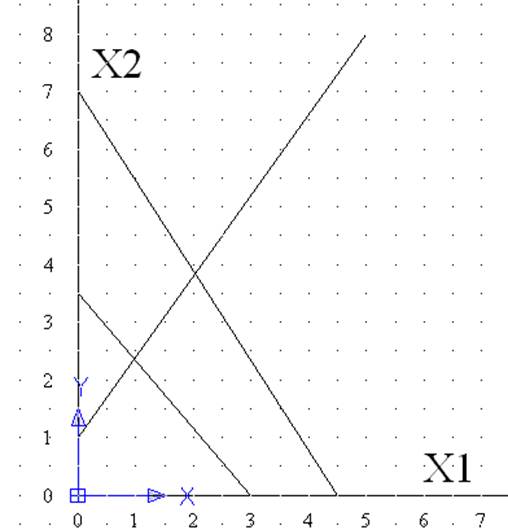
Вариант 5 у=3.5Х1+3Х2
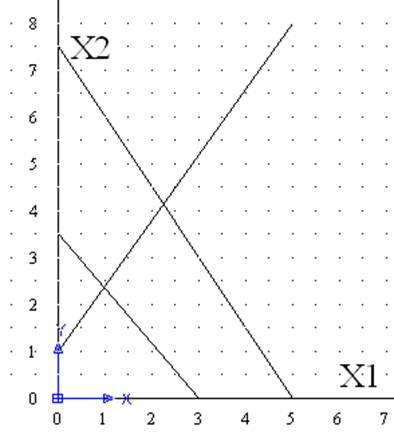
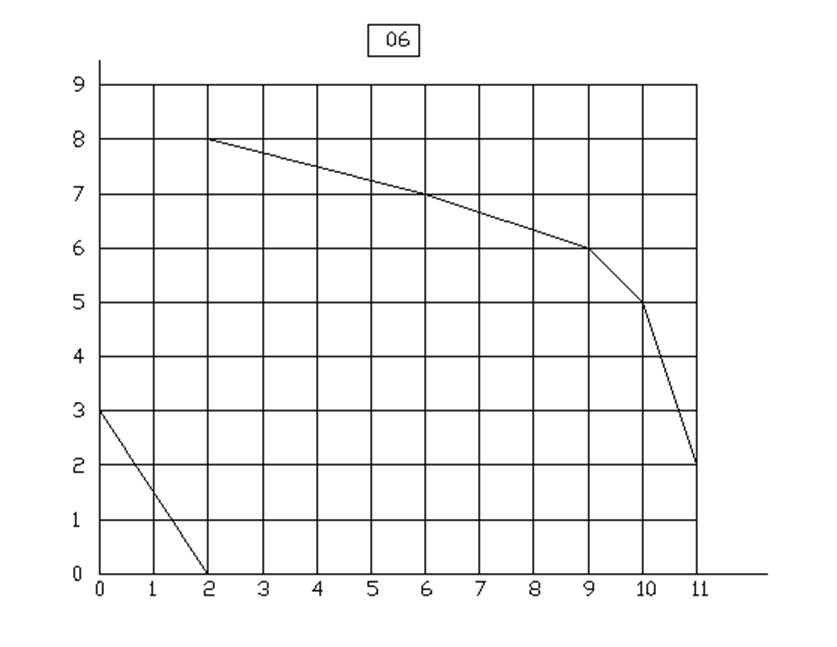
Вариант 6 у=3.5Х1+3Х2
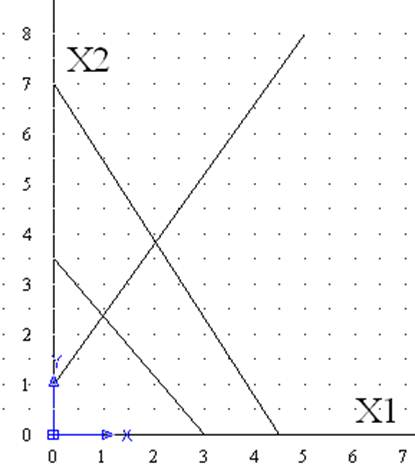
Вариант 7 у=3.5Х1+3Х2
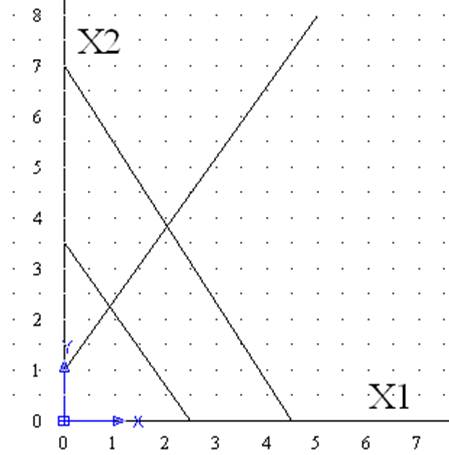
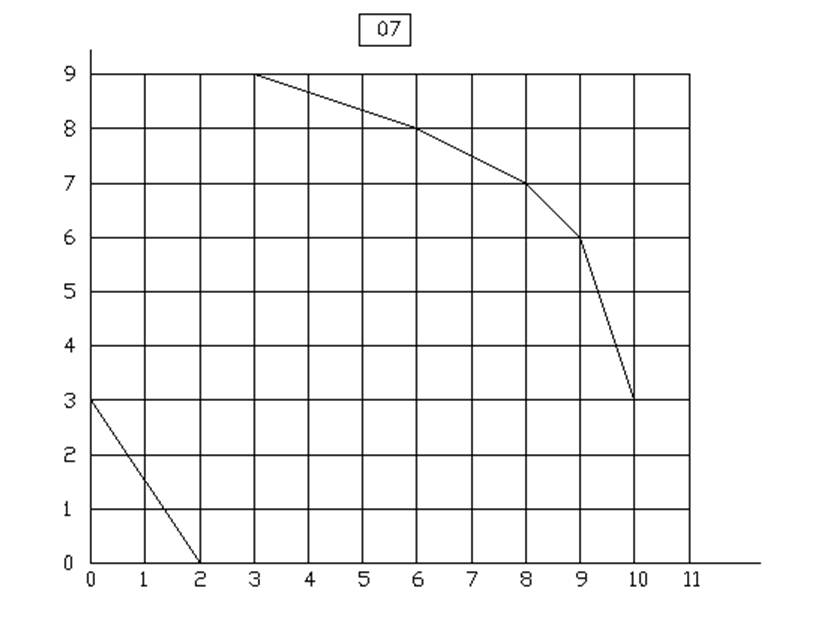
Вариант 8 у=3.5Х1+2.5Х2
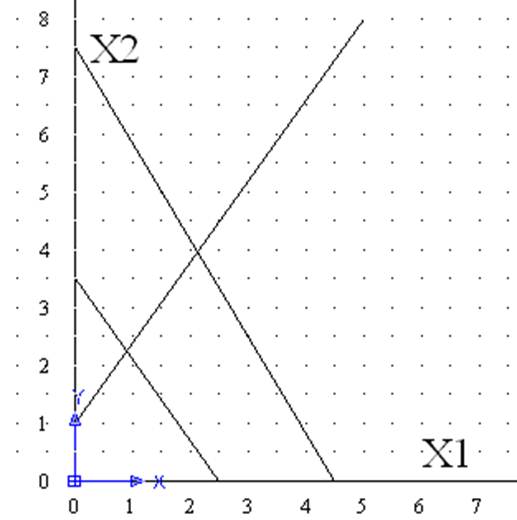
Вариант 9 у=3.5Х1+2.5Х2
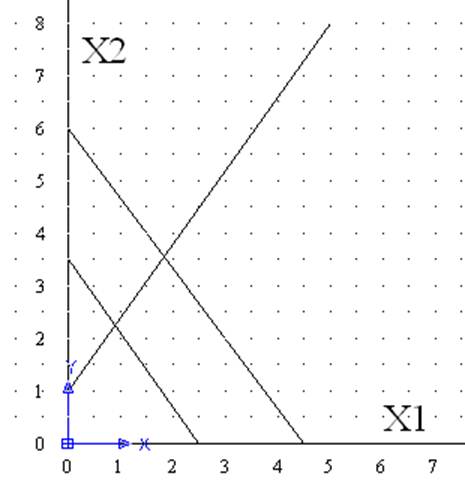
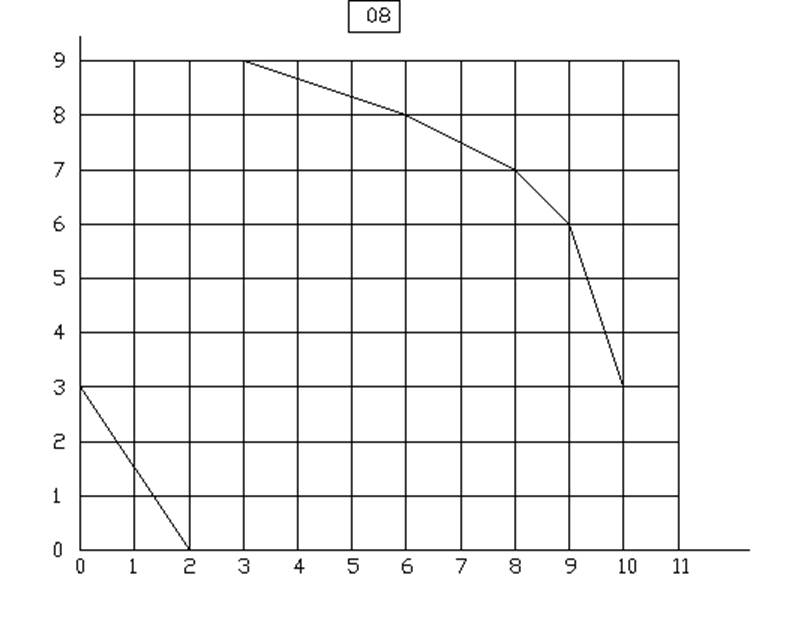
Вариант 10 у=3.5Х1+2.5Х2
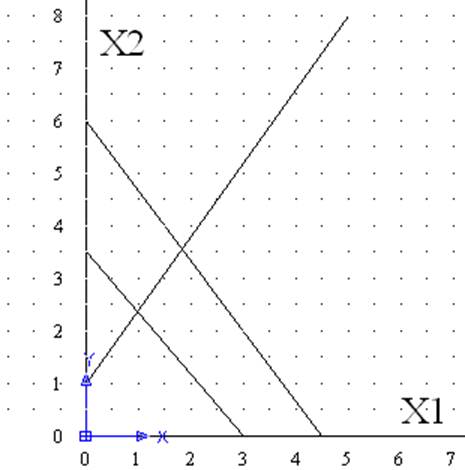
Вариант 11 у=3.5Х1+3Х2

Вариант 12 у=3.5Х1+3Х2
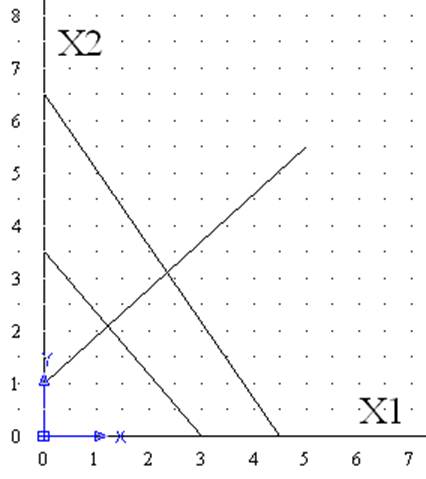
Вариант 13 у=3.5Х1+3Х2
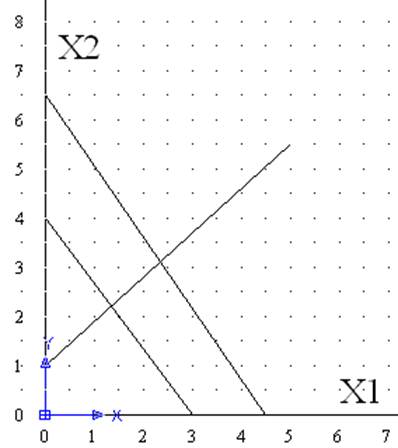
Вариант 14 у=3.5Х1+3Х2
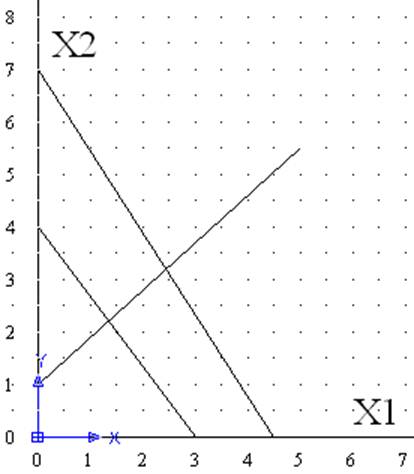
Вариант 15 у=4Х1+3Х2
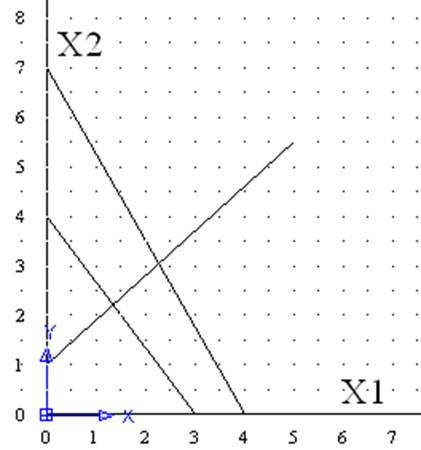
Вариант 16 у=4Х1+3Х2
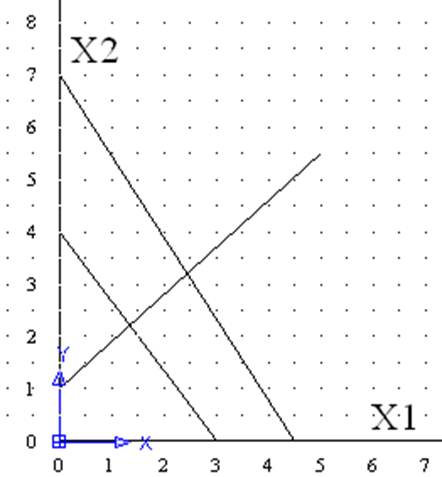
Вариант 17 у=4Х1+3Х2
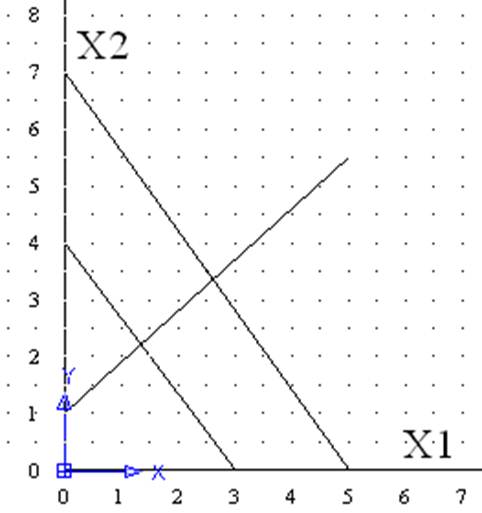
Вариант 18 у=4Х1+3Х2
1 Артамонов Сергей Иванович
1-13
2 Дворников Иван Валентинович
1-7
3. Ильичев Игорь Васильевич
1-2
4 Крылов Дмитрий Иванович
5 Любимов Алексей Сергеевич
1-4 -8
6 Николаев Владимир Юрьевич
7 Новиков Алексей Евгеньевич
1-3-24
8 Пирогов Дмитрий Сергеевич
1-3-16
9 Полозов Алексей Юрьевич
10 Родин Алексей Михайлович
1-2
11 Сатаров Алексей Юрьевич
12 Фофанов Сергей Иванович
13 Черепанов Павел Александрович
14 Шейн Андрей Александрович
1-3-6
15 Василов Артем Георгиевич
16 Морозов Павел Викторович
1-2
17 Петров Борис Леонидович
1-2
18 Рытов Павел Александрович
1-2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.