Исследование простых цепей синусоидального тока

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

КАФЕДРА ТЕОРЕТИЧЕСКИХ ОСНОВ ЭЛЕКТРОТЕХНИКИ

ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2

ПО ТЕМЕ

“ИСССЛЕДОВАНИЕ ПРОСТЫХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА”

ВЫПОЛНИЛИ:                                                                                     ПРОВЕРИЛ:

СТУДЕНТЫ ГРУППЫ 851003                                                       ПРЕПОДАВАТЕЛЬ

МИНСК, 1999

ЦЕЛЬ РАБОТЫ

Приобрести навыки работы с вольтметром, генератором, фазометром. Экспериментально проверить законы распределения тока и напряжения в последовательной, параллельной и последовательно-параллельной цепях гармонического тока.

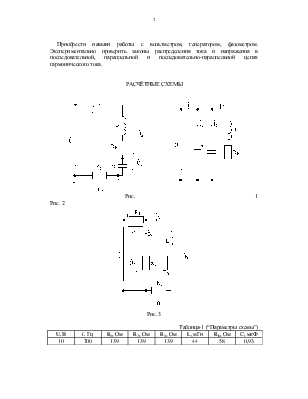
РАСЧЁТНЫЕ СХЕМЫ

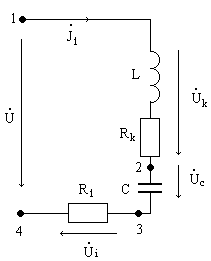
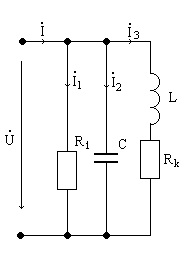
Рис. 1                                                       Рис. 2

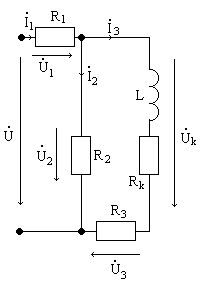
Рис. 3

Таблица-1 (“Параметры схемы”)

ТЕОРЕТИЧЕСКИЙ РАСЧЁТ

1.   Для последовательной цепи на рис.1:

а) Рассчитать сопротивления X_L и X_C реактивных элементов, комплексное входное сопротивление цепи, комплексный ток I и комплексные напряжения элементов U_K, U_c, U_i. Параметры цепи и генератора заданы в “Таблице-1”. Напряжение генератора U=10В. Начальную фазу напряжения генератора принять нулевой.

б) По результатам расчётов построить топографическую диаграмму напряжений всех элементов с указанием вектора тока.

Решение: U=10 (В), f=700 (Гц), R₁=139 (Ом), R_k=58 (Ом), L=44 (мГн), C=0,93 (мкФ)

X_C=1/(wC)=1/(2pfC)=1/(6,28×700×0,93×10^-6)=244,6 (Ом)

Z_C= -jX_C= -j244,6=244,6e^-j90 (Ом)

X_L=wL=2pfL=6,28×700×44×10^-3=193,424 (Ом)

Z_L=jwL=j193,424=193,424e^j90

Z_ВХ=R₁+R_k+jX_l-jX_C=R₁+R_k+j(X_L+X_C)=139+58+j(139,424-244,6)=197-j51,176=

=203,539e^{-j14  30}  (Ом)

J₁=U/Zl_X=(10/203,539e^{-j14  30} )×10^-3 = 49,13e^{j14   30}   (мА)

U₁=J₁R₁=49,13e^{j14   30} ×139×10^-3 = 6,829e^{j14   30}  (В)

Z_k=R_k+jX_L=58+j193,424=201,933e^{j75  20}  ;

U_k=J₁Z_k=49,13e^{j14   30} × 201,933e^{j75  20}  ×10^-3 = 9,92e^{j87   50}    (В)

U_C=J₁Z_C=49,13e^{j14   30}   ×244,6e^j90 × 10^-3 = 12e^{-j75   30}   (В)

Расчёт потенциалов для топографической диаграммы (рис. 4)

Примем j₄=0

j₃=U₁=6,829e^{j14   30} = 6,829(cos14⁰30’  + jsin14⁰30’)=6,61+j1,71

j₂=j₃+U_C=6,61+j1,71+12(cos75⁰30’-jsin75⁰30’)=6,61+j1,71+3-j11,6=9,61-j9,89

j₁=j₂+U_k=j₂+9,92e^{j87   50}  =9,61-j9,89 + 9,92(cos87⁰50’+j9,92sin87⁰50’=9,61-j9,89+0,346+j9,914=9,956+j0,024»10

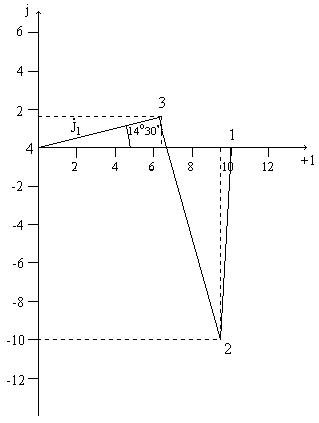
Рис. 4

2.   Для параллельной цепи на рис. 2 и указанных в пункте 1 параметров генератора:

а) Рассчитать по закону Ома комплексные токи I₁, I₂, I₃ ветвей и входной ток I как их сумму б) Построить векторную диаграмму токов и напряжений

Решение: U=10 (В), f=700 (Гц), R₁=139 (Ом), L=44 (мГн), R_k=58 (Ом), C=0,39 (мкФ)

Z_C= -jX_C= -j/(wC)= -j/(2pfC)= -j/(6,28×700×0,93×10^-6)= -j244,6=244,6e^-j90  (Ом)

Z_k=R_k+jwL=58+j2pfL=58+j6,28×700×44×10^-3=58+j193,424=201,933e^{j73  20}   (Ом)

I₁=U/R₁=(10/139)×10^-3=72 (мА)

I₂=U/Z_C=(10/244,6e^-j90   )×10^-3=40,88e^j90  (мА)

I₃=U/Z=(10/201,933e^{j73  20}  )×10^-3=49,5e^{-j73   20} (мА)

I= I₁+I₂+ I₃=72+40,88(cos90⁰+jsin90⁰)+49,5(cos73⁰20’-jsin73⁰20’)=

=72+j40,88+14,22-j47,41=86,22-j6,53=86,47e^{-j4  20}    (мА)

Векторная диаграмма токов и напряжений

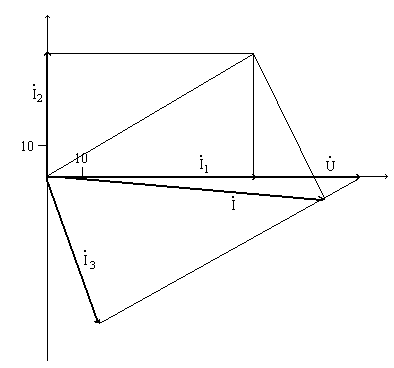
(В 1 см = 10 мА)

Рис. 5

3.   В разветвлённой цепи (рис. 3):

а) Рассчитать, используя метод эквивалентных преобразований, комплексные токи I₁, I₂, I₃ ветвей и комплексные напряжения всех элементов (U₁, U₂, U₃ ¾ напряжения на резисторах R₁, R₂, R₃)

б) Построить топографическую диаграмму напряжений всех элементов и совмещённую с ней векторную диаграмму токов.

в) Составить и рассчитать уравнения баланса активных и реактивных мощностей цепи. Вычислить коэффициент мощности цепи.

Решение: U=10 (В), f=700 (Гц), R₁=139 (Ом), R₂=139 (Ом), R₃=139 (Ом), L=44 (мГн), R_k=58 (Ом)

X_L=wL=2pfL=6,28×700×44×10^-3=193,424 (Ом)

Z_L=jwL=j193,424=193,424e^j90

Z_k=R_k+jwL=58+j193,424=201,933e^{j73  20}  (Ом)

Z₃=R₃+R₄+Z_L=139+58+j193,424=197+j193,424=276,083e^{j44  30}   (Ом)

Z₂₃=(R₂×Z₃)/(R₂+Z₃)=[139(197+j193,424)]/[139+197+j193,424]=

=(27383+j26885,936)/(336+j193,424)=(27383+j26885,936)/(336+j193,424)=

=[(27383+j26885,936)(336-j193,424)]/[336²+193,424²]=

=(9200688-j5296529,392+j9033674,496+5200385,285)/(112896+37412,844)=

=(14401073,285+j3737145,104)/150308,844=95,81+j24,863=98,983e^{j14  35}  ;

Z_ВХ=R₁+Z₂₃=139+95,81+j24,863=234,81+j24,863=236,123^j6   ;

I₁=U/Z_ВХ=10/236,123e^j6  = 42,35e^-j6   (мА)

I₂=(I₁×Z3)/(R₂+Z₃)=(42,35e^-j6×276,083e^{j44   30}  )/(139+197+j193,424)=

=11692,115e^{j38   30}  /(336+j193,424)=11692,115e^{j38   30}  /387,697e^{j29   50} = 30,158e^{j8 40} (мА)

I₃=(I₁×R₂)/(R₂+Z₃)=(42,35e^j6  ×139)/387,697e^{j29  50}  =15,184e^{-j35   50}   (мА)

U₁=I₁R₁=42,35e^-j6×139×10^-3=5,887e^-j6   (В)

U₂=I₂R₂=30,158e^{j8   40}  ×139×10^-3=4,129e^{j8  40}  (В)

U₃=I₃R₃=15,184e^{-j35  50}  ×139×10^-3=2,11e^{-j35   50}   (В)

U_k=I₃Z_k=I₃(R_k+jwL)=15,184e^{-j35  50}  =201,933e^{i73  20}  ×10^-3=3,066e^{j38  30}  (В)

U_L=I₃Z_L=15,184e^{-j35  50} × 193,424e^j90 × 10^-3 = 2,937e^{j54  10}  (В)

Топографическая диаграмма (расчёт)

Принимаем j_А=0

j_В=j_А+I₃R₃=U₃=2,11e^{-j35  50}  =2,11(cos35⁰50’-jsin35⁰50’)=2,11×0,8114-j2,11×0,5855=

=1,712-j1,235;

j_Г=j_В+I₃R₄=1,712-j1,235+15,184e^{-j35 50} ×58×10^-3=1,712-j1,235+