Математика \ Дискретная математика

Минимизация системы булевых функций. Синтез ПЛМ с заданной выходной матрицей, страница 11

Очевидно, что решение данной задачи единственно — это совокупность строк 3, 4 и 8. Ему соответствует интервал — — 00 — — — 1 и интервальный минор (2, 6) х (d, n, о, р) — четвертый элемент минорного покрытия матрицы Y.



Далее аналогичным образом рассматриваются непокрытые единицы строки 6, образующие вместе с соответствующими элементами строки 1 интервальный минор (1,6) х  (с, g, h, j, t), расширить который не удается, затем — непокрытый остаток единиц в строке 1, образующий с соответствующими элементами строки 5 интервальный минор (1,5) x (c, n, q, r), расширенный на столбец с, наконец, все остальные непокрытые единичные элементы матрицы Y входят в интервальный минор (5) x(а, f, l, т, п, p, q, r).

Так находится минорное семиэлементное покрытие матрицы Y.  Переходя от образующих его интервальных к соответствующим парам столбцов в матрицах X* и Y* реализующей системы, получаем следующий результат:

X* =

-

-

1

-

-

-

-

1

-

-

-

-

-

1

1

2

1

-

-

0

-

-

-

3

-

-

-

0

1

-

-

4

1

0

-

-

-

1

-

5

-

-

1

-

-

0

-

6

-

-

-

-

1

-

0

7

-

1

-

1

-

-

-

8

Y* =

0

0

0

0

1

1

0

1

0

0

1

1

0

0

0

2

1

0

0

0

0

0

0

3

1

1

0

0

0

0

0

4

0

0

0

0

0

1

1

5

1

0

0

1

1

0

0

6

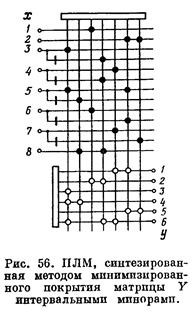
По найденным матрицам легко строится схема, изображенная на рис. 56.


Рассмотренный пример оказался относительно легким, и его удалось решить своеобразным редуцированием, гарантирующим в данном случае оптимальность полученного результата. В более сложных ситуациях описанный метод таких гарантий не дает.

21. Синтез ПЛМ с заданной выходной матрицей

Постановка задачи. Вернемся к рассмотрению задачи построения схемы, генерирующей заданное множество выходных булевых векторов. Ранее мы искали такую схему в классе одноярусных схем, описываемых операторами ВÚ или TÑ, теперь будем искать ее среди ПЛМ—двухъярусных схем, описываемых операторной композицией *) ВÚ T^.

Представляя, как обычно, множество выходных векторов булевой матрицей Y, опишем поведение ПЛМ матричным уравнением

Y = ВÚТ^Х,

в котором все величины, кроме Y, неизвестны.

Синтез искомой схемы сводится к решению данного уравнения, т. е. к нахождению удовлетворяющих ему значений матриц В, Т и X. При этом важно найти не просто некоторое решение (это довольно легко), а по возможности оптимальное решение. Критерием оптимальности в данном случае служат те размеры рассматриваемых матриц, которые можно варьировать.

Допустим, что исходная матрица Y содержит m строк и l столбцов. Обозначив это соответствующей индексацией матрицы (Y = Y(m, l)), укажем аналогичным образом размеры остальных матриц:

Y(m, I) = BÚ (m, р)Т^ (р, n)Х(п, I)

Соседние матрицы в правой части уравнения оказываются равными по значению одного из введенных параметров, что позволяет записать уравнение в более компактной.

*) Выражаясь точнее,  ПЛМ  описывается композицией Ø В^Т^Ø, однако исследование последней сводится к исследованию В^Т^.

Скачать файл