Дифференциальные уравнения (Методические указания к контрольной работе № 7)

Контрольная работа №7

Дифференциальные уравнения

Литература:  [2], гл.ХIII; [4], гл.1;   [5], ч. III,  гл.8.

Основные теоретические сведения

I.   Общим решением дифференциального уравнения первого порядка  называется дифференцируемая функция , которая при любом значении произвольной постоянной  С  является решением данного уравнения. Решения, получающиеся из общего решения   при определенном значении произвольной постоянной  С , называются частными решениями. Задача нахождения частного решения, удовлетворяющего начальным условиям    при  , называется задачей Коши.

а)  Уравнение вида

называется дифференциальным уравнением с разделяющимиcя переменными. Разделив обе части уравнения на , получим общий интеграл уравнения

.

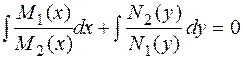б)   Уравнение вида    называется однородным уравнением, если    при любом  . С помощью подстановки  , уравнение приводится к уравнению с разделяющимися переменными.

в)   Уравнение вида   называется  линейным.

Если , то оно называется однородным линейным и его решение может быть получено путем разделения переменных. Если , то уравнение называется линейным неоднородным; его общее решение получается из общего решения соответствующего линейного однородного уравнения с помощью вариации произвольной постоянной интегрирования  С. Данное уравнение можно также решить с помощью подстановки  , где   и   - две неизвестные функции.

2.  При решении дифференциального уравнения высшего порядка необходимо помнить, что его общее решение или общий интеграл содержит столько произвольных постоянных, каков порядок уравнения. С помощью введения новой функции в некоторых случаях можно понизить порядок уравнения, в частности уравнение второго порядка   свести к уравнению первого  порядка, метод решения которого известен.

3.   Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

,                                        (2)

где  - числа.

Задача нахождения решения данного уравнения, удовлетворяющего начальным условиям  ,   , называется задачей Коши.

Если  , то уравнение (2)  называется линейным однородным уравнением. Для его решения составляется характеристическое уравнение

.                                                (3)

а)   Если корни характеристического уравнения   различны и действительны, то общее решение однородного уравнения имеет вид

.

б)   Если корни  , т.е. совпадают, то

.

в)  Если корни   и    комплексные, т.е.  ,  то 

.

Решение линейного неоднородного уравнения (2)  основывается на следующей теореме.

Теорема.      Если   - некоторое частное решение, неоднородного уравнения (2), а    - общее решение соответствующего однородного уравнения, то общее решение уравнения (2)  имеет вид .

Правила для нахождения частного решения   неоднородного уравнения (2) следующие а)  Пусть  .

Если    не является корнем уравнения (3), то частное решение ищется в виде

.

Если   - k-кратный корень уравнения  (3)  , то

   (  или  2).

б)   Пусть   .

Если   не является корнем  уравнения (3), то

.

Если   - корень уравнения  (3), то

.

Здесь числа     находятся в результате подстановки частных решений в исходное уравнение и приравнивания коэффициентов при одинаковых степенях.

4.   Пусть дана система  двух  линейных дифференциальных уравнений с постоянными коэффициентами

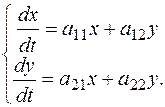                                            (4)

В матричном виде систему (4)  можно записать в виде одного матричного дифференциального уравнения

,

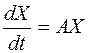где              ,            .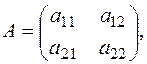

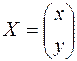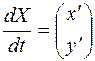Будем искать частные решения в виде  , где   - константы.

Подставляя это решение в систему  (4), получим систему уравнений для определения    и    :

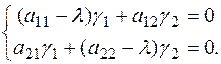
Таким образом, задача нахождения чисел   и    сводится к задаче нахождения координат собственных векторов матрицы  А.  Пусть    и   - собственные векторы  матрицы  А . Тогда общее решение системы (4)  имеет вид 

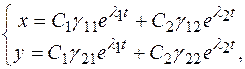
где ,   - корни характеристического уравнения

          .

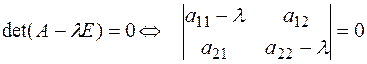В матричном виде  .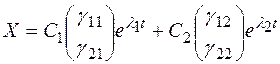

5.   При решении физических задач сначала надо решить, какую переменную нужно принять за искомую функцию. Далее, используя физические законы, составить для ее нахождения