Синтез цифровых схем арифметических устройств, выполняющих операции сложения и умножения над числами, представленными в форме с плавающей запятой в двоичной и двоично-четверичной системах счисления

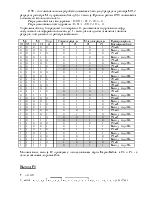
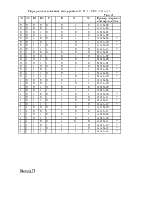
Курсовой проект предполагает синтез цифровых схем арифметических устройств, выполняющих операции сложения и умножения над числами, представленными в форме с плавающей запятой в двоичной и двоично-четверичной системах счисления, в дополнительных кодах.

По исходным данным необходимо разработать и определить:

1.   Алгоритм выполнения операции умножения, для чего потребуется:

Перевести исходные числа из десятичной системы счисления в четверичную;

Представить числа в форме с плавающей запятой;

Произвести умножение чисел согласно заданному алгоритму;

Оценить погрешность вычислений после перевода результата в исходную систему        счисления.

2.   Алгоритм выполнения операции сложения.

3.   Структурную схему устройства, выполняющего сложение и умножение, содержащую узлы для действия над мантисcами и порядками; определить время умножения с учетом временных задержек в комбинационных схемах.

4.   Функциональные схемы основных узлов устройства в заданном логическом базисе. Для этого провести:

Логический синтез комбинационного одноразрядного четверичного сумматора (ОЧС) на    основе составленной таблицы истинности для суммы слагаемых с учетом переноса из младшего разряда, используя при этом карты Карно-Вейча и оценить эффективность минимизации;

Логический синтез одноразрядного четверичного умножителя (ОЧУ) путем минимизации переключательных функций по каждому выходу схемы, используя алгоритм Рота, с последующей оценкой эффективности минимизации;

Логический синтез комбинационной схемы преобразователя множителя(ПМ).

Построить схему ОЧС  в заданном логическом базисе и на мультиплексорах.

Построить схему ОЧУ и ПМ  в заданном логическом базисе.

5.   Время умножения на один разряд и на n разрядов множителя.

2. Исходные данные

Для синтеза устройства, выполняющего операцию сложения и умножения двоично-четверичных чисел в форме с плавающей запятой в дополнительных кодах, были получены следующие исходные данные:

1.   Исходные операнды – десятичные числа с целой и дробной частью, над которыми производится операция умножения: Мн=28,69, Мт=21,59.

2.   Алгоритм выполнения операции умножения ¾ “Б”, (умножение начинается с младших разрядов множителя со сдвигом частичных произведений вправо).

3.   Метод ускоренного умножения : умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах.

4.   Кодирование четверичных цифр двоичными эквивалентами:

0₄ ® 01; 1₄ ® 10; 2₄ ® 11; 3₄ ® 00

5.   Логический базис для реализации ОЧС:

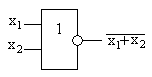
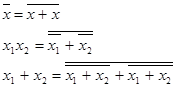
Логический базис для реализации ОЧУ:

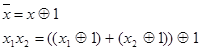
3. Разработка алгоритма умножения

1.   Переведем сомножители из десятичной системы счисления в четверичную:

МНОЖИМОЕ

Мн₁₀ ® Мн₄

Мн₁₀=28,69    Мн₄=130,230             Мн_{2 / 4}= 10 00 01 , 11 00 01

МНОЖИТЕЛЬ

Мт₁₀ ® Мт₄

Мт₁₀=21,59    Мт₄=111,211              Мт_{2 / 4}=01 01 01, 10 01 01

2.   Представим сомножители в форме с плавающей запятой:

Мн      = 0, 10 00 01 11 00 01          P_мн =0. 01 00    +03₁₀ закодирован по заданию 

Мт      = 0, 01 01 01 10 01 01           P_мт =0. 00 11    +03₁₀ закодирован традиционно

3.   Порядок произведения равен сумме порядков множителей:

Результат закодирован в соответствии с заданием на кодировку множимого.

Знак произведения определяется суммой по модулю два знаков сомножителей, т.е.:

зн Мн Å зн Мн = 0 Å 0 = 0 => знак результата “плюс”.

Для умножения мантисс необходимо предварительно преобразовать множитель. При умножении чисел в дополнительных кодах диада 11 (3₄) заменяется на триаду 

Преобразованный множитель имеет вид : Мт^п₄ = или  Мт^п₂ =

Перемножение мантисс по алгоритму “Б” приведено в таблице :

4.   После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение (Мн*Мт₄ = 0,131003320000 P_Мн*Мт4 = 12₄) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:

Мн*Мт₄ = 13100,3320000     P_Мн*Мт = 0;

Мн*Мт₁₀ = 1936, 9681

Результат прямого перемножения операндов дает следующее значение:

Мн*Мт₁₀ = 36,39 * 53,25 = 1937, 7675

Абсолютная погрешность:

∆= 1937,7675 – 1936,9681=0,7994

Относительная погрешность:

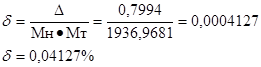
Эта погрешность накоплена за счет приближенного перевода из 10 системы счисления в четверичную обоих сомножителей, а также за счет округления полученного результата произведения.

4. Разработка алгоритма сложения.

1. Представим слагаемые в форме с плавающей запятой:

А₄      = 0,210120                          P_А =+03

А_{2 / 4} = 0, 10 00 01 00 10 01        P_А =0. 01 11    закодированы по заданию 

Б₄     = 0,311100                          P_Б =+03  

Б_{2 / 4} = 0, 11 00 00 00 01 01         P_Б =0. 01 11    закодированы по заданию

2. Проведем сравнение порядков. 

3.   Если порядки не равны необходимо произвести сдвиг мантиссы числа А вправо, если порядок этого числа   меньше, или мантиссы числа Б, если его порядок  меньше. Порядок суммы этих чисел равен большему порядку исходных чисел.

В данном случае сдвиг мантиссы не производится. Однако, во избежание переполнения разрядной сетки увеличим порядок обоих чисел:

А₄      = 0,0210120                          P_А =+10

А_{2 / 4} = 0, 01 10 00 01 00 10 01     P_А =0. 00 01    

Б₄     = 0,0311100                          P_Б =+10  

Б_{2 / 4} = 0, 01 11 00 00 00 01 01     P_Б =0. 00 01   

4.  Получим дополнительные коды слагаемых и произведем их сложение:

[А₄]      = 0,0210120                         

[А_{2 / 4}] = 0, 01 10 00 01 00 10 01         

[Б₄]     = 0,0311100                           

[Б_{2 / 4}] = 0, 01 11 00 00 00 01 01       

Число (А+Б)₄= 0,1121220  ,а его порядок P_{(А+Б) 4} =+04

Для оценки погрешности сложения полученная сумма  приводится