Случайный процесс. Исследование законов распределения случайных процессов

Лабораторная работа № 1.4

ИССЛЕДОВАНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
СЛУЧАЙНЫХ ПРОЦЕССОВ

Случайный процесс – это функция, значения которой в любой момент времени являются случайными величинами. Статистические закономерности, присущие данному виду случайного процесса, можно установить, располагая бесконечным или конечным, но достаточно большим, ансамблем реализаций, путём усреднения соответствующей характеристики. Вероятность того, что в произвольный момент времени t случайный процесс Х(t)  имеет значения, не превосходящие уровень x, определяется одномерным интегральным законом, или функцией распределения F(x, t) . Производная этой функции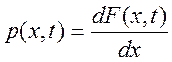 , характеризующая вероятность нахождения значений случайного процесса в момент времени t в интервале (x, x+dx), называется одномерным дифференциальным законом или одномерной плотностью вероятности случайного  процесса в момент времени t.

Случайный процесс, статистические характеристики которого неизменны во времени, называется стационарным. Одномерные функция распределения F(x) и плотность распределения р(х) такого процесса не зависят от времени.

Стационарный случайный процесс, для которого усреднение по ансамблю реализаций даёт тот же результат, что и усреднение по времени для одной реализации достаточно большой длительности, называют эргодическим.

В настоящей лабораторной работе исследуются одномерные  интегральный и дифференциальный законы распределения некоторых видов стационарных эргодических случайных процессов. Для оценки вероятности нахождения процесса в некоторой области значений в лабораторной установке  определяется эмпирическое среднее относительного времени пребывания процесса в рассматриваемой области значений.    Измерение временных интервалов производится  путём счёта формируемых в установке в течение этих интервалов измерительных импульсов.

Порядок выполнения лабораторной работы

Перед началом измерений проверить схему соединений и установить необходимые режимы работы приборов.

Осциллограф GOS-620:  вход «СН 1» подключён к одному из разъёмов «Входной сигнал» лабораторной установки,  переключатель режима «VERTICAL-MODE» – в положении «СН 1», переключатель режима входа «СН 1» – в положении «DС», переключатель режима запуска развёртки «TRIGGER-MODE» – в положении «AUTO», переключатель сигналов синхронизации «TRIGGER-SOURCE» – в положении «СН 1».

Генератор Г3-118:  выход «II» подключён к одному из входов «Входной сигнал» лабораторной установки, переключатель «dB» установлен в положение «10», переключатели  «Hz» и «Множитель» - в положения, соответствующие частоте 1 кГц.

Частотомер Ч3-35 (Ч3-34): вход «А» подключён к разъёму «ВЫХОД» лабораторной установки, переключатель режима работы «РУЧНОЙ – АВТОМАТИЧЕСКИЙ» - в положении «q», переключатель «МЕТКИ ВРЕМЕНИ» - в положении «Вх. А», переключатель «ВРЕМЯ ИЗМЕРЕНИЯ» - в положении «0,1 S», переключатель «РОД РАБОТЫ» - в положении «Частота А», переключатель аттенюатора входа «А» - в положении «1:10», переключатель полярности запуска канала «А» - в положении «П».

Мультиметр  АРРА-203 (205): входные гнёзда «VWHz» и «COM» соединены  с гнёздами «Пороговое напряжение» макета, переключатель режимов - в положении «V=».

Задание 1. Исследование интегрального закона распределения гармонического колебания со случайной начальной фазой

1.1 Включить питание лабораторной установки и приборов (выключатель сети мультиметра АРРА находится на задней панели прибора). Включить питание термостата (тумблер «Ï») частотомера. Переключатель на передней панели установки поставить в положение «Интегральный закон». Наблюдая осциллограмму гармонического колебания на осциллографе, с помощью потенциометра регулировки выходного напряжения генератора

Г3-118 установить амплитуду колебания А = 1,5 В.

1.2  Установить с помощью потенциометров на передней панели установки пороговое напряжение, измеряемое мультиметром,  х = + 2,0 В. Подключить вход осциллографа к разъёму «Выход» установки, отключив от него вход частотомера. Определить параметры

 T =…,  t_и =… наблюдаемой последовательности измерительных импульсов.

1.3  Установить переключатель скорости развёртки «TIME/DIV» в положение «0,2 mS».Уменьшая пороговое напряжение, наблюдать образование бланкируемых интервалов импульсной последовательности вплоть до полного исчезновения импульсов. Установить пороговое напряжение х = 0,0 В. Зарисовать осциллограмму. Измерить отношение длительности пачки импульсов к периоду следования пачек … .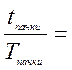

1.4   Подключить вход осциллографа к разъёму «Входной сигнал», а вход частотомера – к разъёму «Выход». Изменяя пороговое напряжение в пределах  х = ( - 1,5 В…+ 1,5 В), определить с помощью частотомера соответствующее  число импульсов n на выходе установки. Результаты измерений внести в таблицу 1.

Таблица 1

х, В	-1.5	-1.2	-0.9	-0.6	-0.3	0.0	0.3	0.6	0.9	1.2	1.5
n(x)
F(x)=10-3·n
F(x)теор..

Задание 2. Исследование дифференциального закона распределения гармонического колебания со случайной начальной фазой

2.1 Переключатель на передней панели установки поставить в положение «Дифференциальный закон». Установить с помощью потенциометров на передней панели установки пороговое напряжение, измеряемое мультиметром, х = 0,0 В. Подключить вход осциллографа к разъёму «Выход» установки, отключив от него вход частотомера. Измерить отношение длительности пачки импульсов к периоду следования пачек … .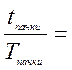

2.2   Подключить вход осциллографа к разъёму «Входной сигнал», а вход частотомера – к разъёму «Выход». Изменяя пороговое напряжение в пределах  х = ( - 1,5 В…+ 1,5 В), определить с помощью частотомера соответствующее  число импульсов n на выходе установки. Определить минимальное и максимальные значения n (см. рисунок).

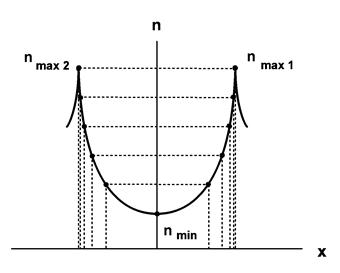
            Рис.  Зависимость числа импульсов на выходе установки от порогового

напряжения при измерении дифференциального закона распределения гармонического колебания со случайной начальной фазой

Разделив область значений функции n(x)на пять интервалов, произвести измерения в соответствующих точках. Результаты измерений внести в таблицу 2.

Таблица 2

n(x)
х, В
p(x)=6,67·10-3·n, В-1
p(x)теор.

Задание 3. Исследование интегрального закона распределения теплового шума

3.1  Выключить генератор Г3-118. Переключатель на передней панели установки поставить в положение «Интегральный закон». Подключить (с помощью преподавателя) генератор шума к разъёму «Входной сигнал» установки. По осциллограмме выборки шума определить наблюдаемую область значений шумового напряжения  rU_max. Рассчитать эмпирическое значение среднеквадратического отклонения шума 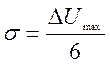. Изменяя пороговое напряжение в пределах  х = ( - 2s…+2s) с шагом, обеспечивающим получение  9…11  значений n(x), произвести измерения числа импульсов n(x). Составить и заполнить таблицу 3, по форме аналогичную таблице 1.

Таблица 3

х, В
n(x)
F(x)=10-3·n
F(x)теор..

Задание 4. Исследование дифференциального закона распределения теплового шума

4.1  Переключатель на передней панели установки поставить в положение «Дифференциальный закон». Изменяя пороговое напряжение в пределах  х = ( - 2s…+2s) с шагом, обеспечивающим получение  9…11  значений n(x), произвести измерения числа импульсов n(x). Составить и заполнить таблицу 4.

Таблица 4

х, В
n(x)
p(x)=6,67·10-3·n, В-1
p(x)теор.