Инвариантность. Комбинированное управление. Количественная оценка инвариантности, страница 3

При полной неопределенности условий работы САУ предлагается использовать либо интегральную оценку вида

, где  - весовая (импульсная переходная) функция;

- амплитудно-фазовая частотная характеристика;

- передаточная функция, либо максимум амплитудной частотной характеристики (АЧХ) на всем диапазоне частот

.                                        (6.23)

Примеры АЧХ абсолютно инвариантной и инвариантной до  систем представлены на рис. 6.11

 

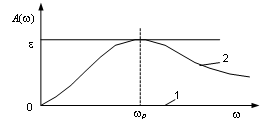Рис. 6.11 - АЧХ инвариантных систем:

1 - абсолютно инвариантной; 2 - инвариантной до

Инвариантность - это свойство систем по преобразованию сигналов. Если исследуется инвариантность САУ по задающему воздействию, то ее свойства сопоставляются с идеальной системой, выход которой абсолютно ковариантен со входом.

Примеры АЧХ абсолютно ковариантной и ковариантной до  систем изображены на рис. 6.12. Обычно используются косвенные показатели, рассмотренные выше (рис. 5.5): - резонансная частота и - показатель колебательности.

Рассмотрим показатели качества (количественные меры инвариантности) селективно инвариантных систем. Селективно абсолютно инвариантные системы имеют нулевую установившуюся ошибку по отношению к рассматриваемым воздействиям ( или ). В селективно инвариантных до  системах значения отличных от нуля установившихся ошибок могут служить количественной мерой их инвариантности.

 

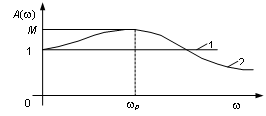Рис. 6.12 - АЧХ ковариантных систем :

1 - абсолютно ковариантной; 2 - ковариантной до

Очевидна аналогия данного подхода оценки инвариантности САУ с исследованием качества переходных процессов, проведенным выше в подразделе 5.2. Действительно, если априорной информации о воздействиях  и  недостаточно и указан только диапазон  существенных частот этих воздействий, то можно использовать оценку (6.23), которая для селективной инвариантности до  перепишется в виде .

Выполнение условий частичной (селективной абсолютной инвариантности) обеспечивает равенство нулю вынужденной (установившейся) составляющей ошибки  системы, однако, как следует из (6.14), на выходе САУ могут наблюдаться переходные процессы . Показателями их качества являются критерии, описанные выше в подразделе 5.2. Для иллюстрации их применимости для исследования проблем инвариантности приведем пример формулировки требований по инвариантности на основе прямых показателей качества, ограничивающих непосредственно переходные процессы (рис. 6.13).

 

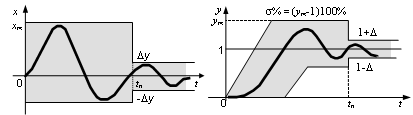             а)                                                                      б)

Рис. 6.13 - Прямые показатели качества инвариантных (а) и ковариантых (б) систем

Вычисление этих показателей проведено в подразделе 3.4. На рис. 6.13 заштрихованы области требований по инвариантности (сравните рис. 6.13, б) и рис. 5.4). Наиболее часто в качестве меры -«расстояния» реальной САУ до абсолютно инвариантной системы используются интегральные критерии качества переходных процессов в САУ.

Описание множества требований к системе, как правило, сводится к определению допустимого отклонения от идеальной желаемой системы. В такой системе мгновенно затухают переходные процессы, управляемая (регулируемая) величина абсолютно инвариантна к возмущениям, а вариации характеристик звеньев системы или их связей не влияют на идеальное поведение системы. Однако сопоставление реальной САУ с идеалом не всегда конструктивно. С позиций практики более конструктивными являются оценки, в которых сравниваются исследуемые процессы  () с желаемыми  (), т.е.

.

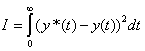Если используются квадратичные функционалы , вида (5.16) и (5.17), безусловные экстремали которых отвечают желаемым процессам  () и для которых , тогда разница  между значениями функционала может служить мерой «расстояния» исследуемой системы от желаемой.

Изложенный подход развивается и по другим направлениям формирования требований к процессам управления в САУ и реализуется в виде желаемой (эталонной) системы.

Таким образом, желаемые системы  учитывают естественную динамику объектов управления и ограничения на переменные.

Системы  задаются типовым (желаемым) распределением корней характеристических полиномов (нулей и полюсов передаточных функций), типовыми (эталонными) временными (переходными) и частотными характеристиками.

Показатели устойчивости и качества процессов управления в САУ являются количественной мерой отклонения  исследуемой системы  от желаемой (эталонной) системы .