Инвариантность. Комбинированное управление. Количественная оценка инвариантности, страница 2

- показательное воздействие (экспонента).

Ограниченную зависимость установившейся реакции САУ  на воздействие  определенного вида, например (6.15), (6.16), рассматривают как селективную инвариантность до .

Селективная инвариантность трактуется как обобщение понятия астатизма САУ на воздействия произвольного вида. Известно, что астатические САУ способны подавлять возмущающие и/или воспроизводить задающие степенные воздействия с нулевой или постоянной установившейся ошибкой. Изображения степенных воздействий (6.15) имеют нулевые полюсы кратности (), . Соответственно, передаточные функции астатических САУ, рассматриваемые от входа  до выхода , имеют нули кратности . В случае селективной инвариантности к воздействию произвольного вида  передаточная функция САУ обращается в нуль на необязательно нулевых полюсах  изображения . При этом селективная абсолютная инвариантность обобщает случай, когда порядок астатизма  превышает степень воздействия  (), а селективная инвариантность до  - случай, когда порядок астатизма равен степени воздействия ().

Из методов построения инвариантных САУ наиболее известно так называемое комбинированное управление.

6.8.2 Комбинированное управление

Под комбинированным управлением (регулированием) понимается такой метод построения замкнутых САУ, когда наряду с регулированием по отклонению или по ошибке используется управление (регулирование) по задающему или возмущающему воздействию. Таким образом, в системе комбинированного управления осуществляется управление (регулирование) по замкнутому и разомкнутому циклам.

Рассмотрим пример (рис. 6.9), когда дополнительно к регулированию по отклонению  используется регулирование по задающему воздействию .

 

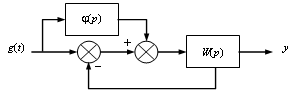Рис. 6.9 - Комбинированная САУ

При отсутствии регулирования по задающему воздействию () регулируемая величина  связана с  через передаточную функцию замкнутой системы:

.                                    (6.17)

Дополнительное введение регулирования по задающему воздействию изменит регулируемую величину следующим образом:

,                (6.18)

т.е. эквивалентная передаточная функция  замкнутой САУ с учетом регулирования по задающему воздействию имеет следующий вид:

.                                                 (6.19)

Преобразуем соотношение (6.19) :

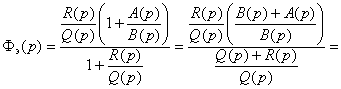
.                                           (6.20)

 в знаменателе передаточной функции дополнительной цепи регулирования по задающему воздействию можно подобрать равным  и сократить. Следовательно, введение регулирования по задающему воздействию не меняет характеристического уравнения САУ, работающей по отклонению, что является замечательным свойством систем комбинированного управления (регулирования). Это означает также, что введение дополнительного регулирования по задающему воздействию не меняет левой части дифференциального уравнения, следовательно, не будут нарушены не только условия устойчивости замкнутой САУ, но и сохранится оценка качества переходного процесса, основанная на использовании корней характеристического уравнения.

Передаточную функцию  эквивалентной схемы комбинированной САУ (рис. 6.10) получим из (6.19) путем несложных расчетов:

, .

Отсюда для передаточной функции по ошибке получим

.                             (6.21)

 

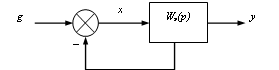Рис. 6.10 - Эквивалентная схема комбинированной САУ

Рассмотренное выше условие абсолютной инвариантности по ошибке  от воздействия  требует, чтобы для рассматриваемой САУ . Из (6.21) следует, что последнее будет выполнено при

.                                                                  (6.22)

Разложив (6.22) в ряд по возрастающим степеням , получим изображение по Лапласу необходимого вида функции, определяющей вводимый сигнал от управляющего воздействия:

.

Ряд может быть конечным и бесконечным.

Таким образом, при введении регулирования по задающему воздействию для получения абсолютной инвариантности необходимо вводить первую и высшие производные от задающего воздействия. Однако абсолютная инвариантность - свойство идеальных систем, которое практически не реализуемо. На практике все работоспособные системы обладают инвариантностью до  и/или селективной инвариантностью, однако количественная мера инвариантности может быть различной.

6.8.3 Количественная оценка инвариантности

Рассмотрим вначале количественные оценки инвариантности до . Логично в качестве таких оценок рассматривать меры отклонения реакций  исследуемой САУ от абсолютно инвариантной системы или, иными словами, предлагается использовать «расстояние» исследуемой САУ до абсолютно инвариантной системы.