








3 ЛИНЕЙНЫЕ ЗАКОНЫ РЕГУЛИРОВАНИЯ.
ТРЕБОВАНИЯ К ПРОЦЕССУ УПРАВЛЕНИЯ
3.1 Понятие о законах регулирования
Под законом
регулирования или, в более общем случае, законом управления понимается
математическая форма преобразований задающих воздействий, возмущений,
воздействий обратных связей, определяющих управляющие воздействия ![]() . Иными словами, это функциональная
зависимость, в соответствии с которой УУ формирует управляющие воздействия
. Иными словами, это функциональная
зависимость, в соответствии с которой УУ формирует управляющие воздействия ![]() . Она может быть представлена в
следующем виде:
. Она может быть представлена в
следующем виде:
![]() ,
(3.1)
,
(3.1)
где ![]() - некоторая, в общем
случае нелинейная, функция от ошибки
- некоторая, в общем
случае нелинейная, функция от ошибки ![]() , задающего
воздействия
, задающего
воздействия ![]() и возмущающего воздействия
и возмущающего воздействия ![]() , а также от их производных и
интегралов по времени. Если функция
, а также от их производных и
интегралов по времени. Если функция ![]() сепарабельная, то
формула (3.1) может быть записана в виде
сепарабельная, то
формула (3.1) может быть записана в виде
![]() .
(3.2)
.
(3.2)
Здесь первое слагаемое соответствует регулированию по отклонению (принцип Ползунова-Уатта), второе и третье - регулированию по внешнему воздействию (принцип Понселе).
Мы рассмотрим только
линейные законы, когда УУ (регулятор) вырабатывает величину ![]() в функции ошибки в соответствии с
линейной формой:
в функции ошибки в соответствии с
линейной формой:
![]() (3.3)
(3.3)
или в операторной форме
![]() .
(3.4)
.
(3.4)
Для упрощения
дальнейшего изложения сделаем следующие предположения о схеме рассматриваемой
САУ. Допустим, что это замкнутая САР и ее функциональная схема соответству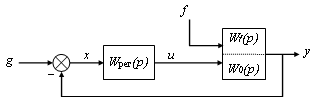 ет рис. 3.1.
ет рис. 3.1.
Рис. 3.1 - Функциональная схема САР
Если допустить, что элемент сравнения отсоединен от ОУ (ОР), то управляющее воздействие определится следующим выражением:
![]() ,
(3.5)
,
(3.5)
где ![]() - рассогласование на
выходе элемента сравнения;
- рассогласование на
выходе элемента сравнения;
![]() - передаточная функция
цепи регулирования.
- передаточная функция
цепи регулирования.
Регулируемая величина может быть найдена из выражения:
![]() ,
(3.6)
,
(3.6)
где ![]() - передаточная функция
ОУ (ОР) по регулирующему воздействию;
- передаточная функция
ОУ (ОР) по регулирующему воздействию;
![]() - передаточная функция
ОУ (ОР) по возмущающему воздействию.
- передаточная функция
ОУ (ОР) по возмущающему воздействию.
Подставляя (3.5) в (3.6), получим:
![]() ,
(3.7)
,
(3.7)
где ![]() - передаточная функция
разомкнутой системы :
- передаточная функция
разомкнутой системы :
![]() .
(3.8)
.
(3.8)
Рассмотрим теперь замкнутую систему, т.е. предположим, что элемент сравнения соединен с ОУ (ОР). При этом
![]() .
(3.9)
.
(3.9)
Решая совместно (3.7) и (3.9), получим для регулируемой величины следующее выражение:
![]() .
(3.10)
.
(3.10)
Аналогично для ошибки получим
![]() .
(3.11)
.
(3.11)
При рассмотрении линейных законов (3.3), (3.4) дополнительно предположим, что ОУ (ОР) представляет собой звено статического типа. Это означает, что в установившемся состоянии между регулируемой величиной и управляющим воздействием существует пропорциональная зависимость, вытекающая из (3.6) при равенстве нулю возмущающих воздействий:
![]() ,
,
где ![]() - коэффициент передачи
объекта управления.
- коэффициент передачи
объекта управления.
3.2 Пропорциональное регулирование
Для простейшего безынерционного УУ закон пропорционального регулирования имеет следующий вид:
![]() .
(3.12)
.
(3.12)
Передаточная функция ![]() может иметь более сложный вид,
например:
может иметь более сложный вид,
например:
![]() .
.
Однако существенным
здесь является то обстоятельство, что цепь регулирования представляет собой
статическое (позиционное) звено и при ![]() ,
, ![]() , где
, где ![]() - коэффициент передачи
цепи регулирования. Заметим, что режим
- коэффициент передачи
цепи регулирования. Заметим, что режим ![]() соответствует
установившемуся режиму, так как приравнивание к нулю оператора
дифференцирования означает приравнивание к нулю всех производных.
соответствует
установившемуся режиму, так как приравнивание к нулю оператора
дифференцирования означает приравнивание к нулю всех производных.
Передаточная функция
разомкнутой системы согласно (3.8) равна: ![]() .
.
В установившемся
состоянии передаточная функция стремится к величине ![]() ,
т.е.
,
т.е. ![]() . Эта величина называется общим
коэффициентом усиления разомкнутой системы и является безразмерной, так же, как
и передаточная функция разомкнутой системы.
. Эта величина называется общим
коэффициентом усиления разомкнутой системы и является безразмерной, так же, как
и передаточная функция разомкнутой системы.
Для установившегося
состояния замкнутой системы при постоянном задающем воздействии ![]() из формулы (3.11) получим следующее
соотношение:
из формулы (3.11) получим следующее
соотношение:
![]() ,
,
где ![]() - установившаяся
(статическая) ошибка;
- установившаяся
(статическая) ошибка;
![]() - установившееся
значение ошибки от возмущающих воздействий в ОУ (ОР).
- установившееся
значение ошибки от возмущающих воздействий в ОУ (ОР).
Поясним в этой связи,
что ошибка (рассогласование) системы ![]() обусловлена (рис.
3.2) как погрешностями реальной аппаратуры, так и самим принципом построения УУ
(регулятора).
обусловлена (рис.
3.2) как погрешностями реальной аппаратуры, так и самим принципом построения УУ
(регулятора).
При этом меняющаяся
в процессе регулирования так называемая динамическая ошибка ![]() в установившемся режиме может
перейти в некоторое постоянное отклонение регулируемой величины от
в установившемся режиме может
перейти в некоторое постоянное отклонение регулируемой величины от ![]() , называемое статической ошибкой
, называемое статической ошибкой ![]() .
.
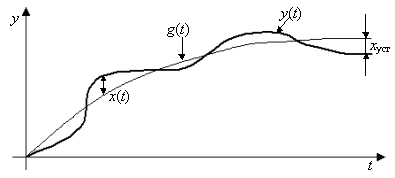
Рис. 3.2 - Процесс управления (регулирования)
Из приведенной выше формулы следует, что пропорциональное регулирование позволяет уменьшить установившиеся ошибки в объекте в (1+К) раз. Регулирование получается статическим, так как при любом конечном значении коэффициента усиления цепи установившаяся ошибка будет отличной от нуля.
Передаточная функция разомкнутой системы (3.8) для пропорционального регулирования может быть представлена в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.