Министерство образования и науки Российской Федерации
Томский Университет Систем Управления и Радиоэлектроники (ТУСУР)
Кафедра автоматизированных систем управления (АСУ)
Отчет по лабораторной работе №1
по дисциплине «Вычислительная математика»
_______
_______
_______
2005
Содержание
Задание …………………………………………………………………………………………………...…3
Краткая теория …………………………………………………………………………………………...…4
Результаты работы …………………………………………………………………………………………6
Приложение А
3
1. Написать программу отделения корней.
2. Написать программу поиска корней (5 методами). Выполнить тестирование. Всё оформить в виде подпрограмм.
Входные данные для головной программы:
-
функция ![]() и её первая и вторая производные;
и её первая и вторая производные;
-
интервал ![]() ;
;
- количество узлов;
-
точность ![]() и
и ![]() ;
;
- метод.
Выходные данные:
- промежутки (интервалы), где есть корни;
-
корни ![]() , точность;
, точность;
-
значения функции ![]() ;
;
- количество итераций n;
-
параметр сходимости 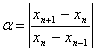 .
.
4
Для поиска приближённого значения корней на промежутке ![]() задаётся сетка
задаётся сетка ![]() и вычисляются значения функции
и вычисляются значения функции ![]() и если для двух соседних точек
выполняется неравенство
и если для двух соседних точек
выполняется неравенство ![]() , то в
интервале ограниченном этими точками расположен по крайней мере один корень
, то в
интервале ограниченном этими точками расположен по крайней мере один корень ![]() .
.
Если считать ![]() , то точность
определения корня равна
, то точность
определения корня равна ![]()
Пусть в интервале ![]() расположен один
корень функции, и его нужно найти с определённой точностью
расположен один
корень функции, и его нужно найти с определённой точностью ![]() .
.
Будем искать корень, вычисляя значения ![]() и
и
![]()
Если выполняется условие ![]() ,
где
,
где ![]() то процесс вычисления
заканчивается, а корень уравнения
то процесс вычисления
заканчивается, а корень уравнения ![]() .
.
Если условие ![]() не выполняется , то
проверяются следующие условия:
не выполняется , то
проверяются следующие условия:
А) если ![]() , то
, то ![]() , и продолжаем процесс деления
интервала
, и продолжаем процесс деления
интервала ![]() ;
;
Б) если ![]() , то
, то ![]() , и продолжаем процесс деления
интервала
, и продолжаем процесс деления
интервала ![]() . Процесс деления продолжаем до тех
пор, пока не будет выполнено либо условие
. Процесс деления продолжаем до тех
пор, пока не будет выполнено либо условие ![]() либо
условие
либо
условие ![]() , где
, где ![]() ,
,
![]() - границы интервала на n-ом
шаге деления исходного интервала. При выполнении условия
- границы интервала на n-ом
шаге деления исходного интервала. При выполнении условия
При заданных двух числах ![]() и
и
![]() . Итерационный процесс будет
строиться по формуле:
. Итерационный процесс будет
строиться по формуле: ![]()
Начальное приближение определяется из условия
![]()
где ![]() равно либо
равно либо ![]() либо
либо
![]() .
.
Если ![]() не задана, то начальное
приближение можно искать по формулам:
не задана, то начальное
приближение можно искать по формулам:
![]()
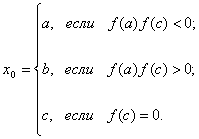
5
Условия завершения
поиска: ![]() ,
, ![]()
Значение корня
равно ![]() .
.
Итерационный процесс строится по формулам:
![]()
![]() , если
, если ![]() - неподвижен
конец
- неподвижен
конец ![]() , или
, или ![]()
![]() если
если ![]() -
неподвижен конец
-
неподвижен конец ![]() .
.
Окончание поиска по условию ![]() ,
где
,
где ![]() - заданная точность. Значение
корня равно
- заданная точность. Значение
корня равно ![]() .
.
Золотое сечение отрезка ![]() осуществляется
двумя точками
осуществляется
двумя точками ![]()
![]() , где
, где ![]() ;
;
![]() - золотое сечение. Алгоритм поиска
нулей функции
- золотое сечение. Алгоритм поиска
нулей функции ![]()
можно представить функции можно представить так:
Полагаем ![]()
![]()
![]()
Шаг первый:
Проверяется условие ![]() , где
, где ![]() - заданная точность.
- заданная точность.
Если данное
условие выполнено, то ![]() . Конец.
. Конец.
Если ![]() не выполнено то переход к шагу 2.
не выполнено то переход к шагу 2.
Ш2: Вычисление координат точек золотого сечения
![]()
![]() и
проверяем условия
и
проверяем условия
![]()
Если выполнено
условие ![]() , то
, то ![]() ;
;
![]() , на первый шаг.
, на первый шаг.
Если выполнено
условие ![]() , то
, то ![]() ;
;
![]() и переход на шаг 1.
и переход на шаг 1.
Исходное уравнение ![]() приводится к
виду
приводится к
виду ![]() , где
, где ![]() ,
а
,
а 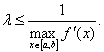 Итерационный процесс идёт по
формуле
Итерационный процесс идёт по
формуле ![]()
![]() .
.
Критерий завершения вычислений имеет вид
![]() где
где ![]() а
а
![]() -заданная точность.
-заданная точность.
6
Результаты работы программы
Входные данные:
Функция: f = exp (x) - 1/x;
Интервал: 0,1 – 2
Точность: 0,0001
Выходные данные:
|
Название метода |
Результат |
Кол-во итераций |
|
Дихотомии |
0,5672 |
15 |
|
Хорд |
0,5672 |
35 |
|
Касательных |
0,5671 |
5 |
|
Золотого сечения |
0,5640 |
11 |
|
Комбинированный |
0,5671 |
4 |
Вывод:
В результате выполнения работы реализованы метод отделения корней, метод дихотомии, метод Ньютона, метод хорд, метод Золотого сечения и метод итераций – поиск корней функции.
Анализ результатов показывает что для исследуемой функции самыми эффективными методами оказались: Метод Ньютона и Метод Итераций. Эти методы находят корни данной функции с за наименьшее число итераций, а следовательно с наименьшими затратами времени.
Приложение А
Листингпрограммы
uses
crt;
type
func=function(i:real):real;
var
i:word;
al,st:real;
const
eps=0.0001;
{====================================== ДИХОТОМИЯ }
function dihot (f:func; a:real; b:real):real;
var
c:real;
begin
i:=0;
repeat
inc(i);
c:=(a+b)*0.5;
if f(c)*f(a)<0 then b:=c else a:=c;
until (b-a)<=eps;
dihot:=c;
end;
{====================================== ХОРД }
function hord(f:func;a,b:real):real;
var
c:real;
begin
i:=0;
repeat
inc(i);
c:=a-f(a)*(a-b)/(f(a)-f(b));
if f(c)*f(b)>0 then b:=c else a:=c;
until f(c)<=eps;
hord:=c;
end;
{====================================== КАСАТЕЛЬНЫХ }
function kasat( f:func; fp:func; fpp:func; a,b:real ):real;
var
c,d:real;
begin
i:=0;
if f(a)*fpp(a)>0 then c:=a
else c:=b;
d:=f(c)/fp(c);
repeat
inc(i);
c:=c-d;
d:=f(c)/fp(c);
until abs(d)<=eps;
kasat:=c;
end;
{====================================== ЗОЛОТОЕ СЕЧЕНИЕ }
function gold (f:func; a:real; b:real):real;
var
c:real;
begin
i:=0;
repeat
inc(i);
c:=abs(a-b)*0.618;
if f(a+c)*f(a)<0 then b:=b-c else a:=a+c;
until (b-a)<=eps;
gold:=b;
end;
{====================================== ИТЕРАЦИИ}
function iter (f:func; a,b:real):real;
var
c,c1:real;
begin
i:=0;c:=a;
repeat
inc(i);
c1:=c;
c:=f(c);
until abs(c1-c)<=eps;
iter:=c;
end;
{====================================== КОМБИНИРОВАННЫЙ }
function komb(f,fp:func;a,b:real):real;
begin
i:=0;
repeat
inc(i);
a:=a-f(a)*(b-a)/(f(b)-f(a));
{if f(c)*f(b)>0 then b:=c else a:=c;}
b:=b-f(b)/fp(b);
until abs(a-b)<=eps;
komb:=a;
end;
{$f+}
function f1(x:real):real;
begin
f1:=exp(x)-1/x;
end;
function fp1(x:real):real;
begin
fp1:=exp(x)+1/(x*x);
end;
function fpp1(x:real):real;
begin
fpp1:=exp(x)-2/(x*x*x);
end;
{$f-}
begin
ClrScr;
writeln('Корни уравнения с точностью: ',eps:7:5);
writeln('найденные методом:');
writeln('(в скобках количество итераций)');
write('дихотомии: ');
gotoxy(20,wherey);
writeln(dihot(f1,0.1,2):7:4,' (',i:3,')');
write('хорд: ');
gotoxy(20,wherey);
writeln(hord(f1,0.1,2):7:4,' (',i:3,')');
write('касательных: ');
gotoxy(20,wherey);
writeln(kasat(f1,fp1,fpp1,0.1,2):7:4,' (',i:3,')');
write('золотого сечения: ');
gotoxy(20,wherey);
writeln(gold(f1,0.1,2):7:4,' (',i:3,')');
{write('итераций: ');
if fp1(2-0.1)<1 then
writeln('x=',iter(f1,0.1,2):7:4,i:3)
else writeln('Корни немогут быть найдены данным методом');
} write('комбинированным: ');
gotoxy(20,wherey);
writeln(komb(f1,fp1,0.1,2):7:4,' (',i:3,')');
readln;
end.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.