Электроснабжение промышленных предприятий: Методические указания к выполнению контрольных заданий, страница 3

В отличие от средней мощности за цикл средняя нагрузка за время q, меньшее длительности цикла, является функцией времени, т.е. зависит от положения начальной точки t интервала q на участке [0, Т_ц], Наибольшее значение Р_мq, т.е. максимум средней нагрузки (мощности) за интервал q, кратко называют q - максимумом, например, десятиминутным Р_м10, или получасовым Р_м30.

Среднеквадратическое значение группового графика мощности за цикл. Так же как и в случае с расчетом величины Р_с  для определения среднеквадратической нагрузки Р_ск за групповой цикл длительностью Т_ц можно использовать формулы (5)-(7) . Среднеквадратическая нагрузка характери- зует эффект нагрева проводника электрическим током, поэтому ее часто называют эффективной нагрузкой и обозначают через Р_э.

Находить значение  как сумму квадратов среднеквадратических значений индивидуальных графиков в общем случае нельзя, т.к.

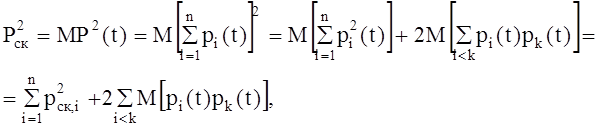         (11)

где M- символ математического ожидания.

В частном случае, когда электроприемники работают независимо друг от друга, будем иметь

                     (12)

и формула (10) примет вид

.                                    (13)

Например, при n=3 получим

.

Возвращаясь к формуле (11), следует отметить, что величена  зависит от попарных взаимосвязей электроприемников, определяющих значе-

ния отдельных слагаемых M_iк. Эти взаимосвязи могут вызвать отклонения величины M_iк от значений, даваемых формулой (12); однако последнее может удовлетворяться и для некоторых зависимых электроприемников. Поэтому условие (12) в / 1 / названо условием некоррелированности, имея в виду, что в частном случае некоррелированные электроприемники могут быть взаимозависимы. Напротив, коррелированные электроприемники всегда зависимы друг от друга.

Дисперсия группового графика нагрузки.  Значение DP можно вычислить по формулам (8) и (10) , подставив  в них вместо  и  соответственно  и . Как и в случае с , суммирование только одних дисперсий индивидуальных графиков для определения дисперсии индивидуальных графиков может привести к ошибкам. Действительно, в соответствии с (11) будем иметь

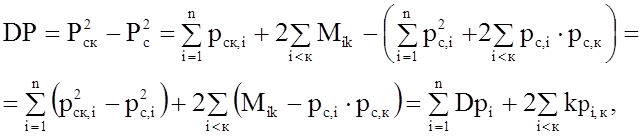          (14)

где - взаимно корреляционный момент двух индивидуальных гpaфиков  р_i(t) и р_к(t).

Очевидно, что если электроприемики независимы, то

.

Коэффициент формы. Как и для индивидуальных графиков, коэффициент формы К_ф группового графика находят по формуле

.

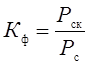Коэффициенты максимума и спроса. Коэффициенты максимума К_м спроса К_с представляют собой отношения

,         ,

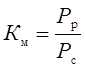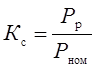где Р_р – расчетная  активная нагрузка;

Р_с – средняя мощность за время группового цикла Т_ц;

Р_ном – суммарная номинальная активная мощность электроприемников.

СОДЕРЖАНИЕ ЗАДАНИЯ

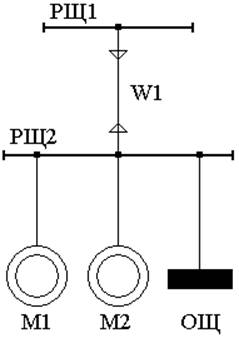Сеть напряжением 380 В (рис.1) питает асинхронные двигатели Ml, M2 номинальной мощностью Р_ном1 и Р_ном2 соответственно, а также прием-                                                                                     

                                        ники освещения, суммарная номинальная ак-

                                        тивная мощность и коэффициент мощности ко-    

                                         торых составляют Р_ном0 и Cosj₀ (линия к щит-            

                                         ку освещения ОЩ). От распределительного 

                                         щита PЩ1 до щита РЩ2 по стенам помещения 

                                         проложен кабель W1 . Каждый из двигателей

                                         имеет график потребляемой активной мощно     

                                         сти, принадлежащий к одному из четырех ти-

                                         пов: периодический, цикличный, не циклич-

                                         ный, не регулярный.

Рис.2. Схема электрической

                  сети.

В задании требуется:

1. Cформировать и построить графики активной мощности двигателей и определить их основные характеристики и показатели.