Обработка экспериментальных данных теплоаэродинамических исследований трубных пучков теплообменников методом наименьших квадратов, страница 2

Nu=0,0425×Re^0,7135.

S(lgNu_оп-lgNu_p)=-0,0032+0,0009+0,0065-0,0075+0,0031=-0,0002.

Определяем среднеквадратическую погрешность на единицу веса:

.

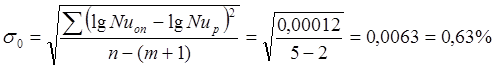Определяем веса параметров:

w_lgC1=D/a₁₁=1,6398/80,818=0,0203;

w_n1=D/a₀₀=1,6398/5=0,3280.

Вычисляем среднеквадратичные ошибки параметров:

s_lgC1=;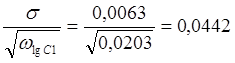

s_n1=.

Определяем доверительный интервал полученной формулы. Задаемся величиной доверительной вероятности p=0,99. Определяем уровень значимости критерия проверки         q=100(1-p)=1%. По значению q=1% и значению n=n-(m+1)=3 находим параметр t=5,840, тогда .

Вычисляем доверительный интервал для дисперсии. По таблице c² – распределения находим для n=3:

;

;

;

;

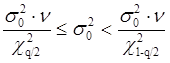9,3×10^-6£<0,0017.

Таким образам с вероятностью 99% среднеквадратичная погрешность эмпирической формулы не превышает 0,0017 или 0,17%.

II.        Произведем подбор эмпирической формулы Eu=c₂×Reⁿ²:

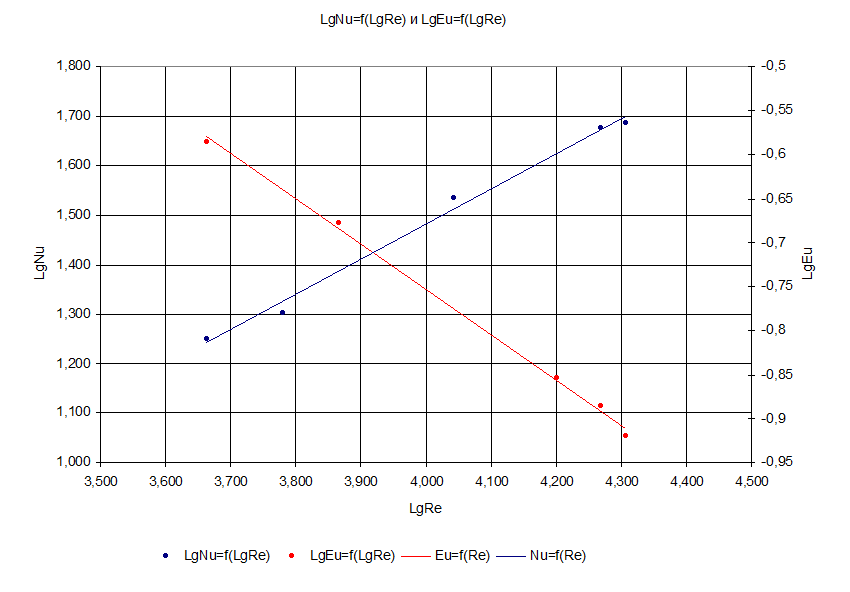
Таким образом, исходя из графика Lg(Еu)=f(Lg(Re)), сразу исключим точки 5, 6 и 10.

Для оставшихся семи точек имеем:

	1	2	3	4	5	6	7	8	9	10
Re	20213	18552	15850	11036			4602	6044	7351
Еuоп	0,12	0,13	0,14	0,15			0,26	0,25	0,21
xк=lg(Re)	4,3056	4,2684	4,2	4,0428			3,6629	3,7813	3,8663
yк=lg(Еu)	-0,9208	-0,8861	-0,8539	-0,8239			-0,585	-0,6021	-0,6778
Еuр	0,1202	0,1259	0,1371	0,1669			0,2682	0,2314	0,2081
dЕu, %	0,1552	-3,1467	-2,0473	11,262			3,1676	-7,4545	-0,928

Вычисляем коэффициенты системы нормальных уравнений:

a₀₀=n=7

a₀₁=åx_k=28,127

a₁₀=åx_k=28,127

b₀=åy_k=-5,345

a₁₁=åx_k²=113,406

b₁=åy_k×х_k=-21,704

Находим значение определителей:

D= a₀₀×a₁₁- a₀₁×a₁₀=7×113,406-28,127×28,127=2,6898

D₀= b₀×a₁₁- a₀₁×b₁=-5,345×113,406-28,127×(-21,704)=3,8079

D₁= b₁×a₀₀- a₁₀×b₀=7×(-21,704)-28,127×(-5,345)=-1,4592

Определяем искомые параметры:

а₀=D₀/D=3,8079/2,6898=1,416

а₁=D₁/D=-1,4557/2,6898=-0,542

с₂=10^(a₀)=10^(1,416)=26,043

n₂=a₁=-0,542

Исключаем также точки 4 и 8.

Для оставшихся пяти точек имеем:

	1	2	3	4	5	6	7	8	9	10
Re	20213	18552	15850				4602		7351
Euоп	0,12	0,13	0,14				0,26		0,21
xк=lg(Re)	4,3056	4,2684	4,2				3,6629		3,8663
yк=lg(Eu)	-0,9208	-0,8861	-0,8539				-0,585		-0,6778
Euр	0,1227	0,1283	0,1391				0,2632		0,2068
dEu, %	2,2834	-1,3166	-0,6182				1,2468		-1,5394
lgЕuоп	-0,9208	-0,8861	-0,8539				-0,585		-0,6778
lgЕup	-0,9110	-0,8918	-0,8566				-0,5796		-0,6845
lgЕuоп-lgЕup	-0,0098	0,0058	0,0027				-0,0054		0,0067

a₀₀=n=5

a₀₁=åx_k=20,303

a₁₀=åx_k=20,303

b₀=åy_k=-3,924

a₁₁=åx_k²=82,764

b₁=åy_k×х_k=-16,096

D= a₀₀×a₁₁- a₀₁×a₁₀=5×82,764-20,303×20,303=1,593

D₀= b₀×a₁₁- a₀₁×b₁=-3,924×82,764-20,303×(-16,096)=2,085

D₁= b₁×a₀₀- a₁₀×b₀=5×(-16,096)-20,303×(-3,924)=-0,821

а₀=D₀/D=2,085/1,593=1,309

а₁=D₁/D=2,1754/3,0965=-0,5156

с₂=10^(a₀)=10^(1,309)=20,3960

n₂=a₁=-0,5156

Значение погрешности для оставшихся пяти точек не превышают 3,5%, следовательно получаем эмпирическую формулу:

Еu=20,3960×Re^-0,5156.

S(lgEu_оп-lgEu_p)=-0,0098+0,0058+0,0027-0,0054+0,0067=0.

Определяем среднеквадратическую погрешность на единицу веса:

.

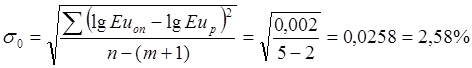Определяем веса параметров:

w_lgC2=D/a₁₁=1,593/82,764=0,0192;

w_n2=D/a₀₀=1,593/5=0,3186.

Вычисляем среднеквадратичные ошибки параметров:

s_lgC2=;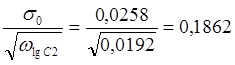

s_n2=.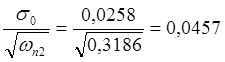

Определяем доверительный интервал полученной формулы. Задаемся величиной доверительной вероятности p=0,99. Определяем уровень значимости критерия проверки         q=100(1-p)=1%. По значению q=1% и значению n=n-(m+1)=3 находим параметр t=5,840, тогда .

Вычисляем доверительный интервал для дисперсии. По таблице c² – распределения находим для n=3:

;

;

;

;

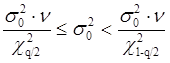0,00016£<0,0277.

Таким образам с вероятностью 99% среднеквадратичная погрешность эмпирической формулы не превышает 0,0277 или 2,77%.