Обработка экспериментальных данных теплоаэродинамических исследований трубных пучков методом наименьших квадратов, страница 2

1. Получить расчетные соотношения для определения параметров конкретных эмпирических формул   и  в соответствии с вычислительной схемой МНК-метода.

2. Определить коэффициенты системы нормальных уравнений для одного из вариантов, представленных в прил.1. Решить систему методом определителей.

3. Рассчитать таблицу отклонений эмпирической формулы от значений заданной функции.

4. Найти среднеквадратичные ошибки полученных коэффициентов в формуле.

5. Определить доверительный интервал полученной эмпирической формулы и доверительный интервал для дисперсии.

4.РАСЧЁТ

1.Исходные данные.

Re-8 вариант,  Nu-9 вариант.

Таблица исходных данных

Параметр	Численное значение при порядковом номере
	1	2	3	4	5	6	7	8	9
Re	19818	18219	13926	9887	8574	3408	3783	4549	5922
Nu	55,4	52,7	44,8	38,4	24,6	20,7	21,7	22,8	28,3

2.Расчёт.

Параметр	Численное значение при порядковом номере
	1	2	3	4	5	6	7	8	9
Re	19818	18219	13926	9887	8574	3408	3783	4549	5922
Nu	55,4	52,7	44,8	38,4	24,6	20,7	21,7	22,8	28,3
	4,30	4,26	4,14	4,00	3,93	3,53	3,58	3,66	3,77
	1,74	1,72	1,65	1,58	1,39	1,32	1,34	1,36	1,45

1.Вычисляем коэффициенты системы нормальных уравнений:

2. Находим значения определителей:

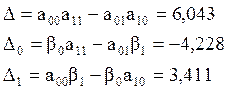
3.Определяем искомые параметры:

Тогда получаем следующую эмпирическую зависимость:

4.Составляем таблицу отклонений эмпирической формулы от заданных значений функции

Таблица отклонений

Параметр	Численное значение при порядковом номере
	1	2	3	4	5	6	7	8	9
Re	19818	18219	13926	9887	8574	3408	3783	4549	5922
Nuоп	55,4	52,7	44,8	38,4	24,6	20,7	21,7	22,8	28,3
Nuр	52,96	50,50	43,41	35,78	33,01	19,62	20,81	23,09	26,79
δNu %	4,40	4,17	3,10	6,82	-34,19	5,22	4,10	-1,27	5,34

Откинем точку под №5 и проведем аналогичные расчёты.

1.Вычисляем коэффициенты системы нормальных уравнений:

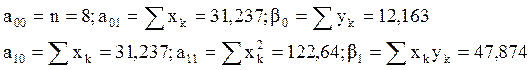
2. Находим значения определителей:

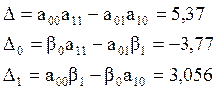
3.Определяем искомые параметры:

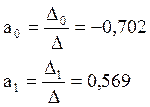
Тогда получаем новую эмпирическую зависимость:

4.Составляем таблицу отклонений эмпирической формулы от заданных значений функции

Таблица отклонений

Параметр	Численное значение при порядковом номере
	1	2	3	4	5	6	7	8
Re	19818	18219	13926	9887	3408	3783	4549	5922
Nuоп	55,4	52,7	44,8	38,4	20,7	21,7	22,8	28,3
Nuр	55,34	52,75	45,27	37,25	20,32	21,57	23,95	27,59
δNu %	0,11	-0,09	-1,05	2,99	1,84	0,60	-5,04	2,51
	1,744	1,722	1,651	1,584	1,316	1,336	1,358	1,452
	1,743	1,722	1,656	1,571	1,308	1,334	1,379	1,441
	0,000	0,000	-0,005	0,013	0,008	0,003	-0,021	0,011

. В нашем случае

5. Определяем среднеквадратичную погрешность на единицу веса:

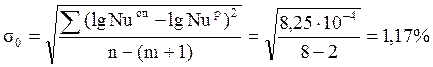
6.Определяем веса параметров:

7.Вычисляем среднеквадратичные ошибки параметров:

8. Определяем доверительный интервал полученной формулы. Задаемся величиной доверительной вероятности p=0,99. Определяем уровень значимости критерия проверки q=100(1-p)=1%, следовательно, t=  3,707.  Тогда 

9.Вычисляем доверительный интервал для дисперсии.

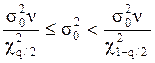
Таким образом, для рассматриваемого примера с вероятностью 99% среднеквадратичная погрешность эмпирической формулы не превышает 0,035 или3,5%.

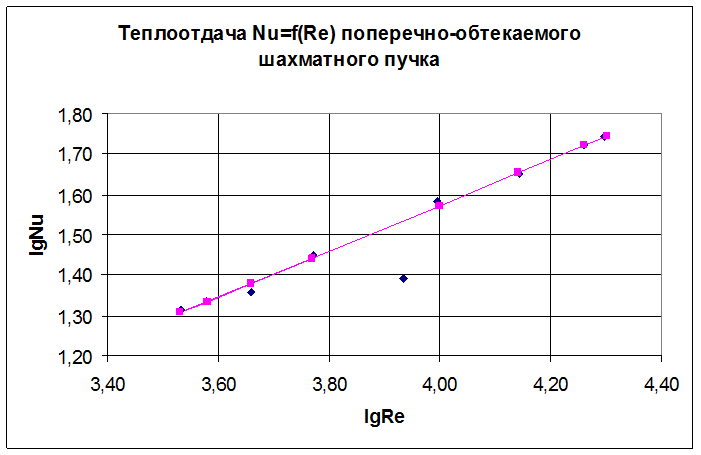
10.Строим графическую зависимость