Министерство образования и науки Российской Федерации
Архангельский государственный технический университет
Факультет промышленной энергетики
Кафедра промышленной теплоэнергетики
Лабораторная работа №8
“Обработка экспериментальных данных теплоаэродинамических исследований трубных пучков методом наименьших квадратов”
Выполнил студент
ФПЭ 3-1
Проверил
Архангельск 2004
1. ЦЕЛЬ РАБОТЫ
Цель работы состоит в ознакомлении и практическом применении МНК-метода для теплоаэродинамических исследований трубных пучков.
Перед выполнением работы необходимо изучить основные математические положения метода и разобраться в типовой вычислительной схеме этого метода.
На основе
экспериментальных данных
определить параметры эмпирических формул ![]() ,
, ![]() и
рассчитать величины отклонений
эмпирических формул от опытных значении.
и
рассчитать величины отклонений
эмпирических формул от опытных значении.
Вычислить среднеквадратичные ошибки полученных коэффициентов в формуле. Определить доверительный интервал полученных эмпирических формул и доверительный интервал для среднеквадратичного отклонения, вычисленного в результате обработки опытных данных.
2. ПОРЯДОК РАСЧЕТА ПАРАМЕТРОВ ЭМПИРИЧЕСКОЙ ФОРМУЛЫ И ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ ПОЛУЧЕННОЙ ФОРМУЛЫ
Имеется функция, которая задана совокупностью опытных
значений ![]() . Необходимо найти эмпирическую формулу
с параметрам, а0, а1, . . . , аm.
. Необходимо найти эмпирическую формулу
с параметрам, а0, а1, . . . , аm.
Схема МНК-метода состоит из следующих этапов:
1. Выбирается или задается вид эмпирической формулы, например
![]() (вид
функции линейный).
(вид
функции линейный).
2. Записывается выражение для квадратичного функционала:
![]()
Для решения задачи аппроксимации значения весовых функций в точках считают одинаковыми.
3. Записывают необходимые условияминимума:
![]()
4. Путем дифференцирования получаем систему нормальных линейных уравнений:
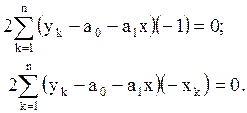
Производим преобразования:
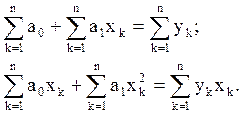
получаем систему уравнений:
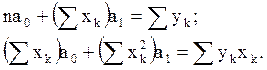
5. Решается система уравнений.
Решить систему уравнений можно методом матриц или методом определителей и найтиа0 и а1:
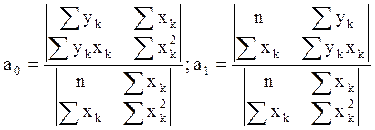
В случае линейной системы нормальных уравнений искомые параметры а0 и а1 являются решением системы
![]()
где ![]() - квадратная матрица системы нормальных
уравнений m+1 порядка ;
- квадратная матрица системы нормальных
уравнений m+1 порядка ;
![]() -
вектор-столбец свободных членов;
-
вектор-столбец свободных членов;
![]() -
вектор-столбец искомых параметров;
-
вектор-столбец искомых параметров;
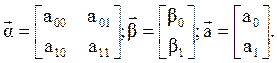
6. Вычисляются отклонения эмпирической формулы от опытных значений функции (%):
![]()
При решении задачи аппроксимации на этом вычисления заканчиваются. Найденная МНК-методом зависимость наиболее вероятна с точки зрения статистической обработки опытных данных.
Определять параметры линейной эмпирической формулы целесообразно и с использованием методов корреляционного и регрессионного анализа, которые позволяют построить доверительные интервалы для параметров и доверительную зону для аппроксимирующей прямой [I] .
При решении задач математической статистики необходимо:
7. Вычислить среднеквадратичную ошибку на единицу веса:
![]()
8. Определить веса неизвестных параметров:
![]()
где det![]() - определитель матрицы
- определитель матрицы ![]() ,
,
А00, А11-алгебраические дополнения к элементам а00, а11.
9. Вычисляются среднеквадратичные ошибки искомых параметров:
![]()
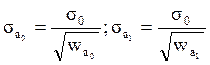
10. Для характеристики
случайных ошибок, возникающих в результате измерений и обуславливающих
рассеивание результатов около аппроксимирующей функции, необходимо определить
доверительный интервал (точность оценки) полученной эмпирической формулы,
задавшись величиной доверительной вероятности (надежность оценки).
Доверительной вероятностью называется вероятность Р того, что искомая величина x
находится в интервале ![]() , который называется
доверительным интервалом (
, который называется
доверительным интервалом (![]() - среднее
арифметическое значение, вычисленное из всего ряда измерений). При большом
числе опытных точек для нахождения доверительного интервала используют
нормальную кривую распределения или функцию Лапласа Ф(t). При
небольшом числе точек доверительный интервал определяется в зависимости от
числа степеней свободы
- среднее
арифметическое значение, вычисленное из всего ряда измерений). При большом
числе опытных точек для нахождения доверительного интервала используют
нормальную кривую распределения или функцию Лапласа Ф(t). При
небольшом числе точек доверительный интервал определяется в зависимости от
числа степеней свободы ![]() и параметра t ,
который носит название критерия Стьюдента [3] . Параметр t
находят по таблице распределения Стьюдента. Доверительный интервал ε определяется
из выражения
и параметра t ,
который носит название критерия Стьюдента [3] . Параметр t
находят по таблице распределения Стьюдента. Доверительный интервал ε определяется
из выражения
![]()
Истинная зависимость ![]() с
вероятностью р заключена в интервале
с
вероятностью р заключена в интервале ![]()
11. Мерой рассеивания исследуемой величины является
величина дисперсии ![]() , которая показывает,
насколько отклоняются отдельные измерения от среднего значения. Корень
квадратный из дисперсии
, которая показывает,
насколько отклоняются отдельные измерения от среднего значения. Корень
квадратный из дисперсии ![]() называют стандартом
или, так же как и
называют стандартом
или, так же как и ![]() среднеквадратичной ошибкой.
При обработке экспериментальных данных необходимо определить доверительный
интервал для среднеквадратичного отклонения опытных данных. При оценке
доверительного интервала дисперсии (квадрата среднеквадратичного отклонения) пользуются
распределением
среднеквадратичной ошибкой.
При обработке экспериментальных данных необходимо определить доверительный
интервал для среднеквадратичного отклонения опытных данных. При оценке
доверительного интервала дисперсии (квадрата среднеквадратичного отклонения) пользуются
распределением ![]() (“хи”-квадрат)
или критерием Пирсона [3] .
(“хи”-квадрат)
или критерием Пирсона [3] .
Доверительный интервал для дисперсии имеет вид
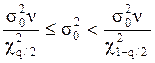
где ![]() -
значения интеграла функции
-
значения интеграла функции ![]() , вычисленные в
интервале от 0 до q/2;
, вычисленные в
интервале от 0 до q/2;
![]() -
то же в пределах от 0 до (1- q/2) ;
-
то же в пределах от 0 до (1- q/2) ;
q - уровень значимости критерия проверки или степень риска;
q=100(1-p)%.
В практике инженерных исследований уровень значимости принимают равным 1 или 5%, что соответствует доверительной вероятности p= 0,99 и p = 0,95. При высокой степени доверия к результатам величину доверительной вероятности выбирают 0,998 - 0,999. Чем точнее требуется результат, тем уже должен быть доверительный интервал.
Следует иметь в виду, что среднеквадратичная ошибка определяется не только погрешностями измерений, но и несовершенством структуры формулы, принятой для описания искомой функциональной зависимости.
3. СОДЕРЖАНИЕ И МЕТОДИКА ПРОВЕДЕНИЯ РАБОТЫ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.