Понятие о статистической информации. Методологические вопросы проведения группировки. Структура статистики финансов

основе приведенных в таблице данных требуется вычислить показатели:

1.  Интенсивные;

2.  Экстенсивные;

3.  Соотношения;

4.  Наглядности.

Решение:

1. Интенсивные показатели:

Используют при изучении частоты встречаемости явления в той или иной среде.

И.П. =   

Для их вычисления недостаточно знать лишь величину интересующего нас явления, необходимо знать еще величину той  среды, в которой данное явление наблюдается.

За абсолютный размер явления будем брать число обращений в каждой группе, за абсолютный размер среды,  продуцирующей явление – численность населения в каждой группе. Расчет проведём в промилях, т.е. вычислим число обращений на каждую тысячу населения.

Расчёты проведём в таблице 1, гр. 4

Таблица 1

2. Экстенсивные показатели:

Характеризуют распределение целого на составляющие его части по их удельному весу, т.е. раскрывают внутреннюю структуру изучаемого явления. Обычно экстенсивные показатели выражаются в процентах.

Э.П. =

Для расчёта Э.П.

-численности населения в опредёлённой группе возраста,  за часть явления будем брать численность населения каждой группы, за целое явление – общую численность населения.

- числа обращений по каждой группе, за часть явления будем брать число обращений, за целое явление – всего обращений.

Расчёты проведём в таблице 2, графы 4 и 5

                                                                                                    Таблица 2

3. Показатели соотношения:

Характеризуют численное  соотношение двух, не связанных между собой  совокупностей, сопоставляемых только логически по их содержанию. По методике вычисления показатель соотношения сходен с интенсивным показателем, хотя они различны по существу.

ПС = 

Показатель      соотношения используется для оценки обеспеченности населения медицинской помощью ( больничными койками, врачебными кадрами, и др.).  Вычисляется  на 10000 населения.

Общая численность населения: 22500, общее число педиатрических участков: 15, тогда:

ПС = уч.

Следовательно,  на 10000 населения приходится 6,67 педиатрических участков.

1.  Показатели  наглядности:

Применяют для изучения изменений, происходящих с тем или иным явлением во времени, а также для сравнения двух и более однородных явлений. При этом, в зависимости от поставленной задачи, одна из величин принимается за 100% или за единицу.

Показатели наглядности указывают, на сколько процентов или  во сколько раз одна из сравниваемых величин больше (меньше) другой.

Для расчёта ПН:

-численности населения в опредёлённой группе возраста,  за 100% будем брать численность населения первой возрастной группы, т.е. 3000 чел. и далее сравнивать с этой величиной.

- числа обращений по каждой группе, за 100% будем брать число обращений первой возрастной группы, т.е. 15 обращений и далее сравнивать с этой величиной.

.

Расчёты проведём по формуле: , в таблице 3.

Таблица 3

Задание 5

На основе приведенных данных требуется:

1.  Составить простой вариационный ряд

2.  Вычислить взвешенную среднюю арифметическую

3.  Вычислить среднеквадратичное отклонение ( при условии, что n меньше 30)

4.  Вычислить ошибку средней арифметической

5.  Вычислить коэффициент  вариации и оценить его

Результаты измерения температуры у восьми детей: 36,7; 37,1; 37,0; 37,2; 36,8; 36,9; 36,6; 36,9.

Решение:

1.Составить простой вариационный ряд:

2.Вычислимь взвешенную среднюю арифметическую:                                

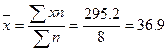
3. Вычислить среднеквадратичное отклонение ( при условии, что n меньше 30):

Вычислим исправленное СКО: - «исправленное» среднеквадратическое отклонение.

- выборочная дисперсия;

σ- выборочное среднеквадратическое отклонение;

- «исправленная» выборочная дисперсия;

- «исправленное» среднеквадратическое отклонение.

5.Вычислить ошибку средней арифметической:

- средняя ошибка выборки, характеризующая отклонение среднего значения признака х от его истинной средней величины.

6. Коэффициент вариации:

Колеблемость признака незначительна и составляет 0,51%, т.к. V<33%, данную совокупность, можно считать однородной.

Задание 6

На основе приведенных данных требуется вычислить показатели динамического ряда по базисному и цепному методам:

1.Абсолютный прирост.

2. Темп прироста.

3. Значение 1% прироста.

4. Темп роста.

Решение:

Рассчитаем средний уровень динамического ряда по формуле средней арифметической, т. к. нам представлен интервальный ряд:

 тыс.

Следовательно, среднегодовой объем составил 2665,4 тыс. абортов.

 Расчёты проведём по формулам:

Абсолютный прирост представляет собой разность двух уровней ряда:

    (1)  - цепная система (к предыдущему году);

       - базисная система (к базисному году);

Темп роста измеряется в процентах и вычисляются по формулам:

       - цепная система (к предыдущему году);

           - базисная система (к базисному году);

Показатели темпов прироста:

Темпы прироста измеряются в процентах и вычисляются по формуле:

, как для цепной так и для базисной системы, гр.6 и 7, табл.2.

Абсолютное содержание 1% прироста по формуле:

, табл. 2, графа 8.

Результаты расчетов удобно поместить в таблицу.

                                                                          Таблица 2.

Рассчитаем средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда:

Рассчитаем среднегодовой абсолютный прирост по формуле:

 (тыс.),

Следовательно, ежегодно уровни ряда убывали в среднем на  164,25  тыс.

Рассчитаем среднемесячный темп роста по формуле:

, где

- среднегодовой коэффициент роста равен: =, где

(б.с.)- заключительный базисный коэффициент роста;

тогда среднегодовой темп роста равен:

=93,96%.

Рассчитаем среднегодовой темп прироста по формуле:

=93,96%-100%= -6,04%

Следовательно, ежегодно уровни ряда убывали в среднем на 6,04%.

Построим график динамического ряда:

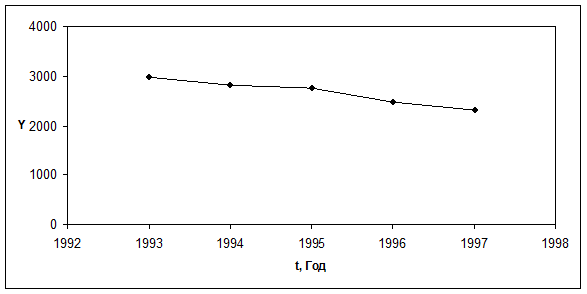
Выводы:

Средний уровень интервального динамического ряда составил 2665,4 тыс. абортов. За данный период времени количество абортов убывало каждый