Основные показатели статистики населения, их значение. Методы исследования применяемые в статистике населения

ряду с неравными интервалами мода определяется в интервале, имеющим наибольшую плотность распределения, и в формуле вместо  , ,  принимаются соответствующие плотности распределения.

Мода и медиана могут быть определены графически: первая- по гистограмме, а вторая — по кумуляте.

Построим гистограмму распределения 200 рабочих по размеру заработной платы, для чего на оси абсцисс построим ряд сомкнутых прямоугольников, у каждого из которых основанием служит величина интервала признака (размер заработной платы в рублях ), а высотой — частота каждого интервала ( число рабочих ). ( Для рядов с неравными интервалами в качестве высоты прямоугольника принимается плотность распределения.)

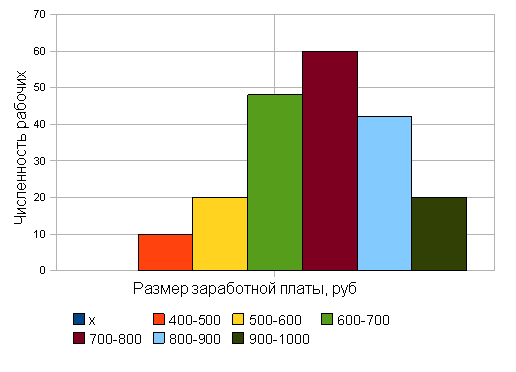
           Рис. Гистограмма распределения 200 рабочих по размеру заработной

                     платы ( графическое определение моды)

В прямоугольнике, имеющем наибольшую высоту, проводим две линии, как показано на рис., и из точки их пересечения опускаем перпендикуляр на ось абсцисс. Значение Х на оси абсцисс в этой точке есть мода ( Мо ).

Для графического отыскания медианы по накопленным частотам строим  кумуляту. 

Для этого из верхней границы каждого интервала на оси абсцисс восстанавливаем перпендикуляр, соответствующий по высоте накопленной частоте с начала ряда по данный интервал. Соединив последовательно вершины перпендикуляров получим кривую, называемую кумулятой. Из точки на оси ординат, соответствующей половине всех частот

(порядковому номеру медианы), проводим прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Опустив из этой точки перпендикуляр на ось абсцисс, находим значение медианы (Ме).

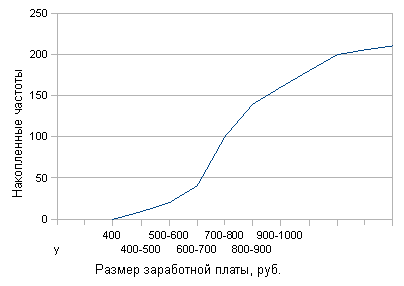
Рис. Кумулята распределения 200 рабочих по размеру заработной платы

         ( графическое определение медианы )

4) Найдем :

5)  Определим

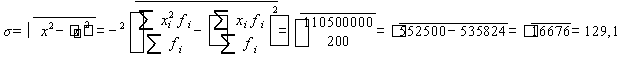
6)  Определим коэффициент вариации:

Задача 3

     Имеем данные по годовой производительности труда работника тыс. рублей (y) и текучести кадров (%) -  (х).

1)  построить поле корреляции, нанести линию регрессии

2)  рассчитать уравнение регрессии

3)  рассчитать коэффициент корреляции, коэффициент эластичности.

 Решение:

Для предварительного выявления наличия связи применяют графический метод:

-  в прямоугольных координатах строят точечный график, который называют полем корреляции.

Положение каждой точки на графике определяется величиной двух признаков: текучесть кадров х (по оси ОХ) и соответствующими данными производительности труда у (по оси ОУ)

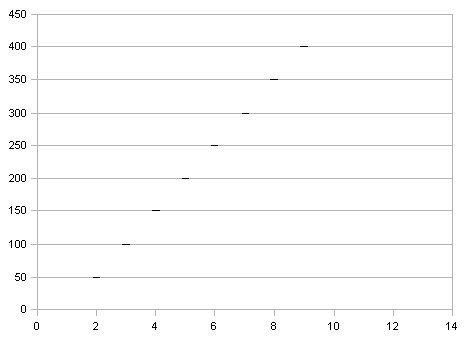
текучесть кадров, %

Рис. Поле корреляции. Линия регрессии.

Покажем теперь на том же графике среднее значение  х и у . Вся плоскость разбилась на 4 части.

  ,

Если точки,, соответствующие значениям отдельных единиц равномерно распределятся по всем четвертям графика, то связь между признаками отсутствует.

В нашем примере видна закономерность: если текучесть кадров ниже среднего            ( х < ), то производительность труда ниже среднего ( у < ). А  где текучесть выше среднего ( х > ), то и  производительность также больше среднего (у > ).

Приблизительное представление о линии связи можно получить на основе эмпирической линии регрессии. В рассматриваемом примере эмпирическая линия регрессии  более близка к прямой., следовательно теоретическая линия регрессии может быть представлена уравнением вида :  у= а + вх

Для нахождения параметров а и в  уравнение регрессии использует метод наименьших квадратов. Критерии которого записываются в виде:

S=→ min , т.е. сумма квадратов отклонений теоретических ( найденных по формуле) значений у от соответствующих опытных значений у_i  должна быть минимальна. Так как у = а + вх, то

S=→ min

Таким образом функция S является функцией двух переменных а и в , а значит достигает экстремума в том случае, если первые частные производные равны нулю, т.е.

После нахождения производных и преобразования полученных выражений приходим к системе нормальных уравнений:

Решая систему находим значения параметров а и в.

Для построения парной линейной регрессии,  необходимо оценить    параметры