S1= 0,494*sin((1/6)*3,14)+ j*1.115*co(s(1/6)*3,14)=0,247+j0.965
S2 = 0,494*sin((3/6)*3,14)+ j*1.115*cos((3/6)*3,14)=0.494
S3= 0,494*sin((5/6)*3,14)+ j*1.115*cos((5/6)*3,14)=0,247-j0.965
S4=0,494*sin((7/6)*3,14)+ j*1.115*cos((7/6)*3,14)=-0,247-j0.965
S5=0.494sin((9/6)*3,14 )+ ј*1.115*cos((9)/6)*3,14) = -0.494
S6=0.494*sin((11/6)*3,14 )+ ј*1.115*cos((11)/6)*3,14) =-0.247+j0.965
Вычисляем полином Гурвица:
V(S)=П(S-Sk) (1.9)
Для этого выбираем те значения, у которых вещественная часть Sk отрицательная.
V(S)=(S- S4)* (S- S5)* (S- S6) В результате подстановки получаем:
V(S)=(S+0.247-j0.965)*(S+0.247+j0.965)*(S+0.494)=
(S2 +S*0.494+0.994)*(S+0.494)=S3+S2*0.988+S*1.28+0.491
Вычисляем нормированное входное напряжение:
Z ВХ=V(S)-h(S)/ V(S)+h(S) (1.10), где h(S) =S3+0.75S-функция фильтрации.
Z ВХ=2S3 +0,988S2+1.238S+0,75S+0,491/ S2 0.988+1.238S+0,491-0.75S=
=2S3 +0,988S2+1.988S+0,491/ S2 0,9882+0,488S+0,491
а) делим числитель на знаменатель:
 2S3 +0.988S2+1,988S+0.491 0.988S2+0.488S+0.491
2S3 +0.988S2+1,988S+0.491 0.988S2+0.488S+0.491
2S3+0.988S2+0.988S 2.024S
S+0.491-первый остаток б) делим делитель на первый остаток
0.988S2+0.488S+0.491 S+0.491
0.988S2+0.488S 0.994S
0.491-второй остаток в) делим второй делитель на второй остаток
S+0.491 0.491
S 2.024S
0.491-третий остаток г) делим третий делитель на 3-й остаток
0,491:0,491=1
Таким образом, мы получили полное
соответствие расчетных значений табличным значениям.
III Расчет ослабления фильтра.
A=10lg(1+(100.1*∆A-1)Ω2n)
Ослабление необходимо рассчитать на частотах:
f0 =3.75*103
f1=3*103
fs=5*103,
1,5f1=4,5*103
2f1 =6*103
![]()
Af1 =10lg(1+(100,1-1)*1)=1дб
Afs=16дб
Af*1.5=10lg(1+(100.1-1)*1.56)=4.68дб
Af*2=10lg(1+(100.1-1)*26)=12.7дб
Af*0=1дб
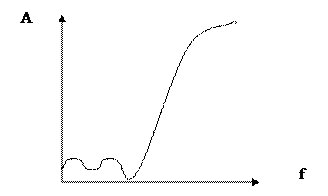
Зависимость ослабления от частоты на рис.1.1.
 |
|||
|
|||
Исходные данные:
· Частота среза f1 =14,4кГц
· Частота задержки fs2=16кГц
· f0=12кГц
· Ослабление в полосе пропускания ∆А=2дб
· Ослабление в полосе задержки As2=15дб.
Расчет.
1. определим неизвестные частоты:
· частота среза fs1
· частота среза f1
· средняя частота f0.
Так как, АЧХ фильтра симметричная, то ∆f1 = f1 -f0 =14.4-12=2.4кГц
f-1= f0-Δf 1=12-2.4=9.6кГц.
∆fs = fs1+ f1=16+14.4=1.6кГц
fs2 = f-1+ ∆fs =9.6-1.6=8кГц
2. нормирование частоты
Ω= k(fs/ f0 - f0/fs) (2.1)
k= f0 /( f1- f-1)-коэффициент преобразования полосы пропускания полосового фильтра
k=12/(14.4-9.6)=2.5
Ω=2.5*(16/12 -12/16)=1.45
3. расчет порядка фильтра
![]() (2.2)
(2.2)
n=15-10lg(100.1*2-1)/20*lg1.45=5.37, округляем до n=6.
3. Из таблицы10 [1] выписываем нормированные значения элементов LC- фильтра нижних частот.
c1=0.5176
l2=1.4142
c3=1.9319
l4=1.9319
c5=1.4142
l6=0.5176
4.Определим нормированные значения элементов полосового фильтра, используя преобразование:
li=kli, ci=1/li (2.3)
li=1/kcj, ci=kcj (2.4)
c6п= l1п=1/2.5*0.5176=0.772
c4п= l3п =1/2.5*1.9319=0.207
c2п= l5п =1/2.5*1.4142=0.282
c5п= l2п =2.5*1.4142=3.53
c3п=l4п =2.5*1.9319=4.82
c1п=l6п =2.5*0.5176=1.294
5.определим коэффициенты денормирования для вычисления истинных значений элементов схемы:
Kl=RН/2*π*f0 (2.5)
Kl=600/2*3.14*12*103=7,96*10-3Гц.
Kc=1/Rн*2*π*f (2.6)
Kc=1/600*2*3.14*12*103*=22.1*10-8Ф.
5. определяем истинные значения элементов:
L3=0.207*7.96*10-3=1.64мГн
L1= Kl* l1=0.772*7.96*10-3=6.14мГн.
L5=0.282*7.96*10-3=2,24мГн
L2=3,53*7.96*10-3=28мГн
L4=4,82*7.96*10-3=38,3мГн
L6=1,294*7.96*10-3=10,3мГн
C1= Kc* c1=1,294*22,1*10-9=28,5*10-9Ф.
C3=4,82*22,1*10-9=106,5*10-9Ф.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.