Ромбическая антенна. Определение основных геометрических размеров антенны

ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Радиотехнический факультет

По дисциплине ПАФУ

НА ТЕМУ:

«Ромбическая антенна»

Руководитель:

Выполнил:

Студент  6 курса гр. Р226

Махачкала  2008

1.Введение

Излучающими элементами ромбической антенны являются длинные провода с бегущими волнами тока и напряжения, расположенные в горизонтальной плоскости по сторонам ромба (рис.1). К одному из острых углов ромба присоединяется сопротивление нагрузки R_н, равное волновому сопротивлению ромба ρ_а, а ко второму острому углу – фидерная линия с волновым сопротивлением ρ_ф, соединяющая антенну с передатчиком.

Направление главного излучения в горизонтальной плоскости совпадает с большой диагональю ромба. Поэтому антенна ориентируется большой диагональю на пункт приёма (нагрузкой в сторону к этому пункту).

Включение сопротивления нагрузки, равного волновому сопротивлению ромба, практически обеспечивает режим бегущей волны на проводах антенны и неизменность её входного сопротивления на всех волнах диапазона.

Распределение поля излучения ромбической антенны в пространстве определяется интерференцией волн от четырёх излучающих проводов, расположенных по сторонам ромба и обтекаемых бегущей волной тока.

Диаграмма направленности повода с бегущей волной тока определяется выраженгием:

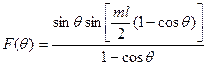                                                   (1.1)

2. СОДЕРЖАНИЕ РАСЧЁТА

По исходным данным следует определить геометрические параметры антенны (длина стороны l, острый угол ромба 2φ₀, высота подвеса ромба над землёй h), диаграммы направленности в вертикальной и горизонтальной плоскостях, границы рабочего диапазона волн, сопротивление излучения и коэффициент полезного действия, коэффициент направленного действия и коэффициент усиления антенны. Кроме того, необходимо рассчитать нагрузочную и фидерную линии и определить диаметр проводов ромба.

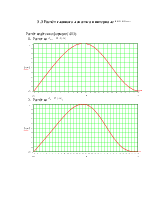
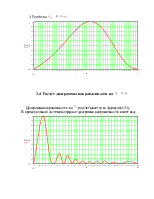
            3. ДИАГРАММА НАПРАВЛЕННОСТИ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ. ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ АНТЕННЫ.

Данная методика определения диаграмм направленности и сопротивления излучения ромбической антенны не учитывает затухание амплитуды тока вдоль проводов ромба. В таком приближении результирующая нормированная диаграмма направленности в вертикальной плоскости определяется выражением:

          (4.1)

,где

-угол, отсчитываемый от линии горизонта,

_д - действующая длинна антенны,

- множитель, учитывающий влияние земли,

- высота подвеса антенны над землёй,

- половина острого угла ромба,

- длина стороны ромба.

Для исследования выражение (4.1) целесообразно представить следующим образом:

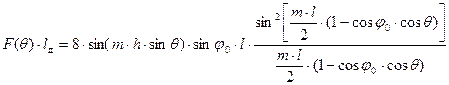                        (4.2)

Исследуя величину и направление главного лепестка, не будем учитывать множитель , который изменяется медленно с изменением угла . Примем, что направление максимума главного лепестка определяется максимумом функции:

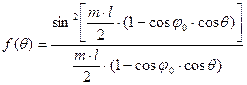                                                                  (4.3)

Впоследствии будет показано, что выбор высоты в аргументе множителя  обеспечивает на оптимальной длине волны равенство , где - направление максимума главного лепестка на . При этом условии множитель  не оказывает существенного влияния на основной лепесток в интервале углов вблизи главного максимума.

Взяв от функции (4.3) производную по  и приравняв её нулю, имеем:

Полученное трансцендентное уравнение вида  имеет ряд решений, которые дают возможность определить углы  для всех максимумов диаграммы направленности. Минимальное значение корня этого уравнения соответствует максимуму главного лепестка . Переводя значения  в радианы и приравнивая ему величину , получаем:

                                                        (4.4)

откуда следует, что:

                                                                                      (4.5)

Из этого выражения видно, что при заданном угле между сторонами ромба длина его сторона должна быть тем больше, чем ближе к горизонту расположен максимум главного лепестка (чем ближе ) и чем больше длина волны .

Подставляя значение  и  из формулы (4.5) в выражение (4.2) и учитывая, что в направлении главного максимума , получаем в общем виде выражение для действующей длинны антенны:

    (4.6)

Из формулы (4.6) следует, что условие наибольшего значения действующей длины антенны имеет место, когда два последних сомножителя будут максимальными.

Приравнивая единице, получим соотношение , которому можно удовлетворить лишь на одной длине волны диапазона. Это делается для оптимальной длины волны . Обозначив угол наклона максимума главного лепестка к горизонту на оптимальной длине волны через , получим:

                                (4.7)

Чтобы определить максимум множителя , находим его производную по , приравниваем её нулю и получаем условие:

Это соотношение опять-таки стремятся выполнить на оптимальной длине волны, для которой оно будет иметь вид:

                                         (4.8)

При выполнении соотношений (4.7) и (4.8) выражения (4.5) и (4.6) принимают следующий вид:

 ,                   (4.9)

 .                     (4.10)

Воспользовавшись формулами (4.8) и (4.9), имеем определённую величину стороны ромба  и острого угла ромба . Подставив эти величины в формулу (4.4), определяем из неё значение косинуса угла наклона максимума главного лепестка к горизонту на какой-либо волне диапазона :

                                            (4.11)