p2=p3+a1![]() +a2
+a2![]() +a3
+a3![]() ;
;
где a1=![]() ;
;
a2=![]() ;
; ![]()
a3=![]() .
.
Запишем уравнение баланса расходов для узла У2:
Qвх2=Qвых2;
![]() ;
;
![]() ;
;
![]()
![]() ;
;
Из последнего уравнения выразим p2:
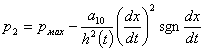 ;
;
p1=pмах;
a10=![]() ;
;
Dз – диаметр золотниковой пары.
Подставив p2 в уравнение баланса давлений, получим:
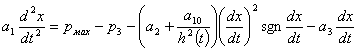 ;
;
Запишем уравнение баланса расходов для узла У3:
Qвх3=Qвых3+Qд3;
![]() ;
;
![]() ;
;
![]() ;
;
![]() (влиянием температуры пренебрегаем);
(влиянием температуры пренебрегаем);
V3 – объем жидкости сосредоточенной в узле У3. Он будет складываться из объема заполняющего трубопровод и переменного объема жидкости в цилиндре.
![]() ;
;
z0 – расстояние между поршнем и крышкой в начальном положении;
![]() - коэффициент податливости;
- коэффициент податливости;
Ea – базовый модуль упругости (при 20![]() и 0.1МПа Ea=1.7*109Па);
и 0.1МПа Ea=1.7*109Па);
ap – коэффициент, учитывающий влияние давления на модуль упругости (ap=10)
Подставляя составляющие уравнения баланса расходов У3, получим:
![]() ;
;
Выразим из последнего уравнения p3, получим:
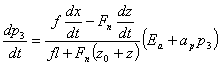 ;
;
Таким образом математическая модель будет представлять собой систему уравнений:
 |
![]() ;
;
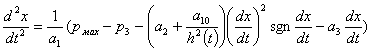 ;
;
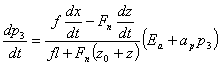 ;
;
Систему будем решать с помощью ЭВМ, используя метод Рунге-Кутта в соответствии с алгоритмом, схема которого представлена на рисунке. Результаты расчета представлены в приложении.
Так как метод Рунге-Кутта позволяет решать уравнения 1-го порядка, необходимо понизить порядок путем замены переменных. Путем понижения порядка она должна быть преобразована к системе состоящей из 5-ти уравнений.
Введем массивы функций и массивы производных:
Таблица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перепишем уравнения с учетом принятых обозначений:
DZ[1]:=Z[2];
DZ[2]:=![]() ;
;
DZ[3]:=Z[4];
DZ[4]:=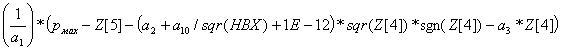 ;
;
DZ[5]:=![]() ;
;
 |
|||
![]() Привод
Привод ![]()
![]() Входное воздействие
Входное воздействие
![]() (COD,S1,S2,pмах )
(COD,S1,S2,pмах )
![]() Расчет (Тмах,
Расчет (Тмах,![]() t, NU…)
t, NU…)
 |
![]()
|
![]() уравнений
уравнений
|
![]()
![]()
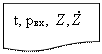
![]()
![]()
![]()
|
|
 |
|||||
Печать результатов для
![]()
![]()
![]()
![]()
|
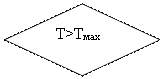 |
НЕТ
ДА
Рис. Схема алгоритма программы для решения дифференциального уравнения
Время переходного процесса tп =0.32 с;
Перерегулирование:
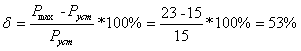 ;
;
Время достижения первого максимума tmax=0.03 с.
Время нарастания переходного процесса: tн=0.018 с.
Декремент затухания:
![]()
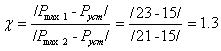
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.