Пластинчатый регулируемый насос гидропривода многоцелевого станка (Определение параметров гидронасоса), страница 2

Считая  что  ротор  и  пластины  условно  как  диск   с  диаметром   ,  а  зазор  между  ротором  и  дисками  0.006 мм   одинаковым  ,  получим  :

                     

г) Потери  на  трение  пластин в пазах ротора

Примем  зазор  между  пластиной  и  ротором  мм.  Считая , что пластин  на  участке  всасывания  и  нагнетания  участвует 10 штук,  имеем:                             

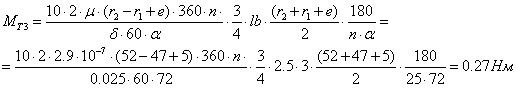
21.76 + 0.00523 + 1.67 = 23.44 Нм

Механический  КПД :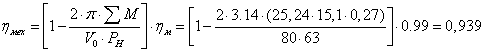

4.3   Расчет   гидравлического  КПД .

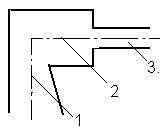При  протекании  жидкость  последовательно  проходит  всасывающее  отверстие (как  диффузор  )  , кольцевые  отверстия ,  затем  попадает  в  рабочую  камеру .

1-  входное  отверстие , S₁= 0,0011 м²

2-  кольцевидные  отверстия , S₂=  0.0002 м²

3-  отверстие  в  рабочей  камере , S₃= 0,0000785 м²

Теоретическая подача:      

Средняя  скорость  течения  жидкости :                                                                                                                                                                                                                                                                                                                                                    

      

     

Так  как  длинна  трубопроводов  мала ,учитываем  потери  давления  только  от  местных  сопротивлений  .На  них . Считая  течение  жидкости  на  участке 1-3  турбулентным , то суммарные  потери  определяются  по  формуле :

        

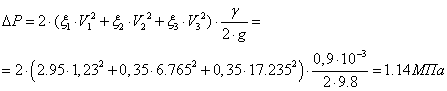
Гидравлический КПД  : 

4.4  Общий  КПД  гидронасоса

            

5.  Прочностной расчёт деталей насоса

5.1  Расчет  пластин   на  изгиб

Максимальный  крутящий   момент  в  месте  заделки  пластин  определим   по  формуле  :

                                                                                                                                                                                                                                                                                              

где   S -  толщина  пластины,  принимаем   S = 2 мм;

Напряжения  в  опасном  сечении:

 Допустимое   напряжение на изгиб для пластины из быстрорежущей стали Р18 составляет

[ ]  =  250 МПа;  В нашем случае расчётное напряжение  удовлетворяет условию: 

 = 111  МПа   <  [ ]  - следовательно   прочность  обеспечена .

5.2  Расчет  контактных  напряжений

   Пластина  соприкасается  со  статором  в  точке  А (рис    ),  которая  определяется  углом      ротора , при  котором  имеет  место  наибольший  угол  наклона  профиля  статора  :

                     ,       О₁ОС =  

                        

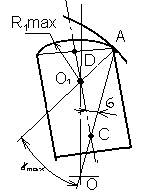угол     ,  внутри  которого  расположена  кривая  профиля  статора 

 

Максимально  допустимый  радиус  закругления  пластины :

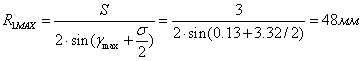
     Оптимальный радиус  вершин пластины  составляет (3 5 мм ) .
Рис.      Расчетная   схема                                                         Примем   R₁= 5 мм  ;

пластины                                

          Контактные  напряжения  по  линии  контакта  пластины  и  статора  при  E = 105 МПа:

      

  0.35 МПа < [ ]  =  250 МПа  прочность  обеспечена.

В итоге этой проверки на прочность пластин, мы оставляем те параметры пластины, которые были приняты выше, т.к. прочность обеспечивается.

5.3  Прочностной расчет вала

    Считаем , что на  вал  насажена  шестерня , создающая  реактивную силу и  окружную ,  принимаем диаметр начальной окружности d =25 мм  угол  зацепления  ⁰.

 Вал  передает  момент  М= 89,17Нм,    

                         

Неуравновешенная  составляющая  силы, передаваемой  муфтой:

              

Опорные реакции в вертикальной плоскости:

;   ;  

;     ;   

Проверка: ;   -1202 + 2163.6  - 961.6 = 0;

     

Строим  эпюру изгибающих моментов в вертикальной плоскости; 

Опорные  реакции  в  горизонтальной  плоскости :

        

                

        

          

Проверка  3897 – 5944,6 + 3897 -1783 ,4 = 0;

Строим эпюру изгибающих моментов в горизонтальной плоскости. Находим  опасное сечение, вычислив суммарный изгибающий и момент крутящий:  

Опасным сечением является сечение 2. Из условия на прочность . Определим необходимый диаметр вала в опасном сечении

                                                      

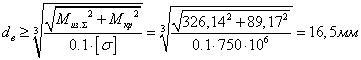    ; принимаем  d =25 мм

Данный  диаметр  вала  обеспечивает  безотказную  работу  насоса ,  так  как 

выдерживает  необходимые  нагрузки.

Определяем  пределы  выносливости  стали:

при изгибе:

при кручении: 

Нормальное напряжение в сечении под шестерней для симметричного цикла:

            

Момент сопротивления:

            

Момент сопротивления: при кручении: