Ректификация. Построение диаграммы фазового равновесия в координатах y – x. Определение числа теоретических тарелок в колонне

  ,                                              (15)

где  - коэффициент распределения (константа фазового равновесия) -го компонента при температуре и давлении наверху колонны;  - мольная доля компонента в паре на верху колонны, в случае полной конденсации пара в дефлегматоре ; q – число компонентов системы.

Температура внизу колонны  определяется из уравнения изотермы жидкой фазы:

;                                           (16)

где  - коэффициент распределения -го компонента при температуре и давлении низа колонны.

Если сырье поступает в колонну при температуре начала кипения смеси, т.е. доля отгона сырья на входе в колонну  равна нулю, температура сырья  определяется по уравнению изотермы жидкой фазы (16). Если сырье поступает в колонну при температуре конца кипения смеси, доля отгона сырья на входе в колонну  равна единице, температура сырья  определяется по уравнению изотермы паровой фазы (15). Если сырье поступает в колонну в виде парожидкостной смеси, т.е. , температура сырья на входе в колонну  определяется из уравнения:

;                                              (17)

или                                       ;                                              (18)

где  - коэффициент распределения - го компонента при температуре и давлении в зоне питания колонны.

Уравнение (17) лучше использовать для значений доли отгона, больших 0,5; а уравнение (18) дает лучшие результаты при значениях доли отгона, меньших 0,5.

Коэффициенты распределения  зависят от температуры, поэтому уравнения (15) – (18) при расчете температур  решаются методом последовательных приближений.

1.4. Построение диаграммы фазового равновесия в координатах

   y – x

В процессах простой перегонки и ректификации равновесные концентрации фаз определяются зависимостью:

,                                                  (19)

где    - мольная концентрация - го компонента в паре, равновесном с жидкостью состава .

В случаях, когда разделяемую смесь можно считать идеальной, т.е. для всех компонентов смеси выполняется закон Рауля, коэффициент распределения рассчитывается как отношение давления насыщенного пара компонента  при фиксированной температуре к общему давлению в системе :

.                                                      (20)

Для идеальных смесей зависимость между равновесными составами фаз выражается уравнением Рауля-Дальтона:

.                                                   (21)

Для многих жидких смесей расчет коэффициента распределения можно производить по уравнению (20), если общее давление в системе  (5 ат)^м.

Давления насыщенных паров индивидуальных веществ  или зависимости для их расчета приведены в работах [1-6].

Для бинарных смесей, подчиняющихся закону Рауля, диаграмму фазового равновесия в координатах y-x (рис. 1.2) строят по следующему алгоритму. Температурный режим выкипания разделяемой смеси определяется как разность температур кипения чистого низкокипящего  и чистого высококипящего  компонентов при выбранном давлении в системе . В этом интервале от  до  принимается ряд значений температуры (обычно десяти значений бывает достаточно). Для каждой температуры определяются значения давления насыщенных паров компонентов  и рассчитываются из соотношения (20) коэффициенты распределения низкокипящего компонента. Мольная концентрация низкокипящего компонента  в жидкости, кипящей при выбранной температуре и давлении ; рассчитывается из соотношения

,                                              (22)

где ,  - давления насыщенных паров соответственно высококипящего и низкокипящего компонентов.

После этого из соотношения (21) определяется мольная концентрация низкокипящего компонента в паре , равновесном с жидкостью. Далее строится диаграмма фазового равновесия в координатах y-x ( рис. 1.2).

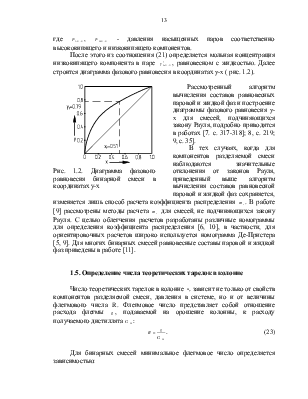
Рис. 1.2. Диаграмма фазового равновесия бинарной смеси в координатах у-х

Рассмотренный алгоритм вычисления составов равновесных паровой и жидкой фаз и построение диаграммы фазового равновесия y-x для смесей, подчиняющихся закону Рауля, подробно приводятся в работах [7. с. 317-318]; 8, с. 219; 9, с. 35].

В тех случаях, когда для компонентов разделяемой смеси наблюдаются значительные отклонения от законов Рауля, приведенный выше алгоритм вычисления составов равновесной паровой и жидкой фаз сохраняется,