Ректификация. Определение диаметров штуцеров. Определение толщины тепловой изоляции колонны. Насадочные ректификационные колонны непрерывного действия

Определение площади поверхности теплопередачи кипятильника и дефлегматора

Кипятильник.

Принимаем коэффициент теплопередачи от греющего пара к кипящей жидкости   [7, с. 169]. Расчетная площадь поверхности теплопередачи кипятильника  определяется по уравнению (66):

 .

Принимаем в качестве кипятильника кожухотрубчатый испаритель с паровым пространством, имеющий площадь поверхности теплообмена   [2, табл. 5.12].

Запас площади поверхности теплообмена кипятильника:

.

Дефлегматор.

Расчетная площадь поверхности теплообмена в дефлегматоре  складывается из площади поверхности, необходимой для конденсации паров , и площади поверхности, необходимой для охлаждения конденсата  (рис. 2.2):

.

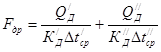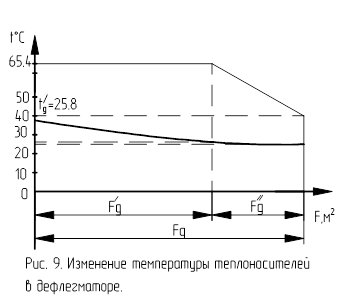
Принимаем коэффициент теплопередачи в зоне конденсации паров  , а в зоне охлаждения конденсата   [7, с. 169].

Тепловой поток в зоне конденсации паров (см. тепловой баланс колонны подраздел 1.7):

 .

         Тепловой поток в зоне охлаждения конденсата:

 .

Проверка:

 .

         Температуру в конце зоны конденсации паров  можно найти из уравнения:

.

Средняя разность температур в зоне конденсации паров  и в зоне охлаждения конденсата :

         Расчетная площадь поверхности теплопередачи дефлегматора:

 .

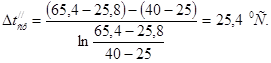
Принимаем в качестве дефлегматора одноходовой кожухотрубчатый теплообменник с площадью поверхности теплообмена:   [2, табл. 5.9].

Запас площади поверхности теплообмена составляет:

3.1. Насадочные ректификационные колонны

непрерывного действия.

При расчете насадочных ректификационных колонн непрерывного действия исходными обычно являются те же данные, что и в случае расчета тарельчатых колонн.

Построение кривой равновесия, рабочих линий верхней и нижней частей колонны и, следовательно, определение оптимального флегмового числа выполняют аналогично.

Диаметр колонны. Диаметр колонны D определяют в зависимости от количества и скорости поднимающихся паров. Средний расход пара находят решением системы уравнений материальных балансов по методике, изложенной для тарельчатых колонн.

Оптимальную скорость пара, соответствующую началу эмульгирования (точка нагрузки), вычисляют по уравнению, полученному на основе анализа и обобщения результатов многих исследований:

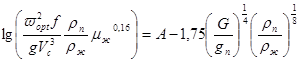.                           (67)

В выражении (67): ω_opt – оптимальная скорость паров, отнесенная к полному сечению колонны,  м/с; ƒ – удельная поверхность насадки, м²/м³; V_c – свободный объем насадки, м³/м³; ρ_п, ρ_ж – плотность соответственно пара и жидкости, кгс/м³; μ_ж – динамическая вязкость жидкости при средних условиях, Па·с; А = – 125 – постоянная для парожидкостных смесей; G, g_п – масса соответственно жидкости и паров, кг/ч; g – ускорение свободного падения, м/с².

Удельная поверхность и свободный объем насадки зависят от формы и размеров насадочных тел. Характеристики некоторых насадок приведены в таблице 3.1.

Характеристики насадок                                                                   Таблица 3.1

Диаметр колонны вычисляют по формуле

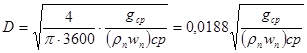.                      (68)

3.2. Расчет высоты насадочной части колонны

Высоту насадки Н можно определять двумя методами:

1)  нахождением числа теоретических тарелок Ν_т (ступеней изменения концентрации) и высоты насадки h_т, эквивалентной одной теоретической тарелке (ВЭТТ);

2)  нахождением числа единиц переноса z и высоты насадки h_z, эквивалентной одной единице переноса (ВЕП).

При использовании метода определения ВЭТТ высоту насадки Н определяют как произведение числа теоретических тарелок Ν_т на высоту насадки h_т , эквивалентную одной теоретической тарелке (ВЭТТ):

                            Н = Ν_т h_т  .                                                            (69)

Число теоретических тарелок Ν_т (ступеней изменения концентрации) находят способом, изложенным в методике расчета тарельчатых колонн.

Высоту насадки h_т , эквивалентную одной теоретической тарелке, для условий, соответствующих точке нагрузки (начало эмульгирования), определяют по уравнению, полученному на основе обработки многочисленных опытных данных:

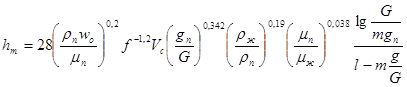 ,        (70)

где m – среднее значение тангенса угла наклона к оси χ кривой равновесия смеси в координатах χ – γ .

Величину m с достаточной точностью можно найти спрямлением участков кривой равновесия (заменой кривой равновесия ломаной линией), при этом:

, где m₁, m₂, m₃… - тангенсы углов наклона прямых на отдельных участках; i – число прямолинейных участков ломаной линии.

При расчете по методу единиц переноса (ВЕП) высоту насадки H определяют как произведение числа единиц переноса z на высоту насадки h_z , эквивалентную одной единице переноса (ВЕП):

H = z · h_z .                      (71)

Общее число единиц переноса z, которое выражает изменение рабочей концентрации одного из компонентов, приходящееся на единицу движущей силы, можно определить из интегральных уравнений:

 ;                           

, где x_р и y_р – равновесные концентрации.

Значение интеграла в уравнении определяют графически; при этом для ряда значений y находят величину:  и строят кривую в координатах:  – y . Площадь, заключенная между кривой, осью абсцисс и ординатами, проведенными через заданные точки y_д и у_к , соответствует искомому интегралу, т.е. числу единиц переноса. Аналогично можно рассчитать и интеграл во втором уравнении.

Высота насадки h_z, эквивалентная одной единице переноса, зависит