Обобщающие статистические показатели. Средние величины и показатели вариации. Ряды динамики

Данный ряд является дискретным, поэтому модой будет варианта с наибольшей частотой – Мо = 9,2.

Данный ряд является четным, в этом случае медиану для дискретного ряда находят по формуле:

.

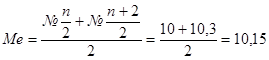3. Показатели вариации.

Для расчета показателей вариации составим таблицу, в которой рассчитаем отклонения , квадраты данных отклонений :

Таблица 2.

№	xi
1	8,9	-1,58	2,4964
2	9,2	-1,28	1,6384
3	10,5	0,02	0,0004
4	14,3	3,82	14,5924
5	14,3	3,82	14,5924
6	10,3	-0,18	0,0324
7	9,2	-1,28	1,6384
8	8,9	-1,58	2,4964
9	9,2	-1,28	1,6384
10	10	-0,48	0,2304
Итого	104,8		39,356
В среднем	10,48

Рассчитаем дисперсию:

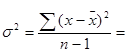39,356/9 = 4,373.

Рассчитаем стандартное отклонение:

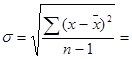2,091.

Рассчитаем коэффициент вариации:

 = 2,091/10,48*100 = 19,953%.

Задача 3. Имеются данные о заработной плате по предприятию:

Вариант 5
Интервал руб.	Число рабочих
3300-3350	15
3350-3400	48
3400-3450	70
3450-3500	26
3500-3550	30
3550-3600	38
3600-3650	22
3650-3700	19
3700-3750	27
3750-3800	29

Рассчитать:

1.  Средний уровень заработной платы.

2.  Моду и медиану.

3.  Показатели вариации:

•  дисперсию;

•  среднее квадратическое отклонение;

•  коэффициент вариации.

Решение.

Запишем распределение, определим средины интервалов хі:

Таблица 1.

xi	fi
3325	15
3375	48
3425	70
3475	26
3525	30
3575	38
3625	22
3675	19
3725	27
3775	29

1. Определим средний уровень зарплаты. Вспомогательные данные:

Таблица 2.

	xi	fi	xi*fi
	3325	15	49875
	3375	48	162000
	3425	70	239750
	3475	26	90350
	3525	30	105750
	3575	38	135850
	3625	22	79750
	3675	19	69825
	3725	27	100575
	3775	29	109475
Итого		324	1143200

Для расчета среднего значения используем формулу среднюю арифметическую взвешенную:

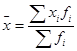 =1143200/324 = 3528,4 руб.

2. Мода определяется по формуле:

 руб.

нижняя граница модального интервала;

h – интервал группирования, у нас равен 50;

частоты модального, передмодального и послемодального интервалов.

Мода определяет величину наиболее вероятного значения зарплаты – 3566,7 руб.

Медиану определим по формуле (медианный интервал – такой, в котором суммарная частота начинает превышать половину суммы всех частот):

 руб.

 нижняя граница медианного интервала;

 суммарная частота передмедианного интервала;

 частота медианного интервала.

Значение медианы в данном случае характеризует средину распределения работников по величине зарплаты.

3. Вспомогательные данные для определения показателей вариации:

Таблица 3.

	xi	fi	xi*fi	(xi-xsr)	(xi-xsr)^2*fi
	3325	15	49875	-203,395	620543,3
	3375	48	162000	-153,395	1129442
	3425	70	239750	-103,395	748337,7
	3475	26	90350	-53,3951	74126,85
	3525	30	105750	-3,39506	345,7933
	3575	38	135850	46,60494	82536,77
	3625	22	79750	96,60494	205315,3
	3675	19	69825	146,6049	408367,2
	3725	27	100575	196,6049	1043645
	3775	29	109475	246,6049	1763606
Итого		324	1143200		6076265

Рассчитаем дисперсию:

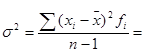6076265/323 = 18811,97.

Рассчитаем стандартное отклонение:

.

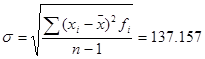Рассчитаем коэффициент вариации:

 = 137,157/3528,4*100 = 3,887%.

Задача 4. Имеются данные о количестве экспертиз, провидимых в среднем, за одну смену одним экспертом. Все эксперты разбиты на группы относительно стажа работы I: до 5 лет, II: 5-15 лет, III: 15 и выше лет.

Вариант 7
I		II		III
№	Штук	№	Штук	№	Штук
1	1	20	1	21	1
2	2	19	2	21	2
3	3	18	3	24	3
4	4	20	4	26	4
5	5	23	5	21	5
6	6	21	6	20	6
7	7	23	7	25	7
8	8	24	8	26	8
9	9	21	9	27	9
10	10	20	10	25	10

Рассчитать:

1.  Дисперсии и среднеквадратические отклонения:

•  общие;

•  внутригрупповые;

•  межгрупповые;

2.  Корреляционное отношение.

3.  Вывод.

Решение.

1. Для определения общей и внутригрупповых дисперсий и среднеквадратического отклонения используем формулы:

;

.

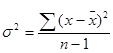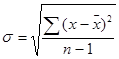Общие показатели, вспомогательная таблица:

Таблица 1.

	xi	(xi-xsr)	(xi-xsr)^2
	20	-3,567	12,721
	19	-4,567	20,854
	18	-5,567	30,988
	20	-3,567	12,721
	23	-0,567	0,321
	21	-2,567	6,588
	23	-0,567	0,321
	24	0,433	0,188
	21	-2,567	6,588
	20	-3,567	12,721
	21	-2,567	6,588
	21	-2,567	6,588
	24	0,433	0,188
	26	2,433	5,921
	21	-2,567	6,588
	20	-3,567	12,721
	25	1,433	2,054
	26	2,433	5,921
	27	3,433	11,788
	25	1,433	2,054
	22	-1,567	2,454
	23	-0,567	0,321
	24	0,433	0,188
	26	2,433	5,921
	28	4,433	19,654
	29	5,433	29,521
	29	5,433	29,521
	27	3,433	11,788
	28	4,433	19,654
	26	2,433	5,921
Итого	707		289,367

Получаем:

=707/30 = 23,567;

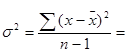289,367/29 = 9,978.

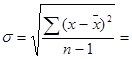3,159.

Для отдельных групп, вспомогательная таблица:

Таблица 2.

I			II			III
Xi	(xi-xsr)	(xi-xsr)^2	xi	(xi-xsr)	(xi-xsr)^2	xi	(xi-xsr)	(xi-xsr)^2
20	-0,9	0,81	21	-2,6	6,76	22	-4,2	17,64
19	-1,9	3,61	21	-2,6	6,76	23	-3,2	10,24
18	-2,9	8,41	24	0,4	0,16	24	-2,2	4,84
20	-0,9	0,81	26	2,4	5,76	26	-0,2	0,04
23	2,1	4,41	21	-2,6	6,76	28	1,8	3,24
21	0,1	0,01	20	-3,6	12,96	29	2,8	7,84
23	2,1	4,41	25	1,4	1,96	29	2,8	7,84
24	3,1	9,61	26	2,4	5,76	27	0,8	0,64
21	0,1	0,01	27	3,4	11,56	28	1,8	3,24
20	-0,9	0,81	25	1,4	1,96	26	-0,2	0,04
209		32,9	236		60,4	262		55,6
Xsr =	20,9		Xsr =	23,6		Xsr =	26,2
	3,656			6,711			6,178
	1,912			2,591			2,486

Определяем среднюю из внутригрупповых дисперсий:

(3,656 + 6,711 + 6,178)/3 = 5,515.

Определяем межгрупповую дисперсию из соотношения:

;

9,978  – 5,515 = 4,463.

Корреляционное соотношение:

4,463/9,978 = 0,447.

То есть  вариация результативного признака на 44,7% обусловлена влиянием фактора – стажем работы эксперта.

Задача 5. По группе водителей имеются следующие данные: численность группы - п; количество имеющих допуск на управление автобусом - m .

Вариант 5
n	M
89	16

Рассчитать долю, дисперсию и среднее квадратическое отклонение исследуемой группы.

Решение.

Рассчитаем долю:

w = m/n = 16/89 = 0.180.

Дисперсия доли:

0,180*0,720 = 0,148.

Среднее квадратическое отклонение доли:

Модульная единица 1.6 Ряды динамики

Задача 6. Имеются данные о изъятии опиатов, за ряд лет, кг.

Год	Выпуск продукции млн.шт. яиц в год
	Вариант 5
1982	7,4
1983	7,9
1984	7,9
1985	9,1
1986	8,9
1987	7,9
1988	8,6
1989	8,7
1990	8,9
1991	9,7
1992	9,9
1993	6,2
1994	6,8
1995	7,2
1996	7,3
1997	7,5
1998	7,6
1999	7,5
2000	7,9
2001	7,8
2002	7,4
2003	7,8
2004	7,4
2005	7,9
2006	7,9

Необходимо рассчитать:

1. Показатели динамики цепным и базисным методами:

•  абсолютный прирост;

•  коэффициент (темп) роста;

•  коэффициент (темп) прироста;

•  абсолютное значение 1% прироста.

2. Средние показатели динамики:

•  средний абсолютный прирост;

•  средний коэффициент (темп) роста;

•  средний коэффициент (темп) прироста;

Решение.

1.    Формулы для расчета показателей динамики:                                                                                          

цепные                                       базисные абсолютного прироста -                                    

темпов роста -                                                 

темпов прироста -                                

абсолютное значение одного % прироста -           

Результаты представим в таблице:

Таблица.

Расчет показателей динамики

Год	уровень ряда у, млн.шт.	Абсолютный прирост		Темп росту,%		Темп прироста, %		Абсолютное значение 1% прироста
		Цеп.	Баз.	Цеп.	Баз.	Цеп.	Баз.
1982	7,4	-	-	-	-	-	-	-
1983	7,9	0,5	0,5	106,76	106,76	6,76	6,76	0,074
1984	7,9	0	0,5	100,00	106,76	0,00	6,76	0,079
1985	9,1	1,2	1,7	115,19	122,97	15,19	22,97	0,079
1986	8,9	-0,2	1,5	97,80	120,27	-2,20	20,27	0,091
1987	7,9	-1	0,5	88,76	106,76	-11,24	6,76	0,089
1988	8,6	0,7	1,2	108,86	116,22	8,86	16,22	0,079
1989	8,7	0,1	1,3	101,16	117,57	1,16	17,57	0,086
1990	8,9	0,2	1,5	102,30	120,27	2,30	20,27	0,087
1991	9,7	0,8	2,3	108,99	131,08	8,99	31,08	0,089
1992	9,9	0,2	2,5	102,06	133,78	2,06	33,78	0,097
1993	6,2	-3,7	-1,2	62,63	83,78	-37,37	-16,22	0,099
1994	6,8	0,6	-0,6	109,68	91,89	9,68	-8,11	0,062
1995	7,2	0,4	-0,2	105,88	97,30	5,88	-2,70	0,068
1996	7,3	0,1	-0,1	101,39	98,65	1,39	-1,35	0,072
1997	7,5	0,2	0,1	102,74	101,35	2,74	1,35	0,073
1998	7,6	0,1	0,2	101,33	102,70	1,33	2,70	0,075
1999	7,5	-0,1	0,1	98,68	101,35	-1,32	1,35	0,076
2000	7,9	0,4	0,5	105,33	106,76	5,33	6,76	0,075
2001	7,8	-0,1	0,4	98,73	105,41	-1,27	5,41	0,079
2002	7,4	-0,4	0	94,87	100,00	-5,13	0,00	0,078
2003	7,8	0,4	0,4	105,41	105,41	5,41	5,41	0,074
2004	7,4	-0,4	0	94,87	100,00	-5,13	0,00	0,078
2005	7,9	0,5	0,5	106,76	106,76	6,76	6,76	0,074
2006	7,9	0	0,5	100,00	106,76	0,00	6,76	0,079

2. Рассчитаем средние показатели динамики.

средний уровень ряда -  млн. шт.

средний абсолютный прирост -  млн. шт.

средний темп роста -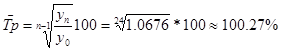            

средний темп прироста-            %.

Таким образом, выпуск продукции за 25 лет в среднем увеличивался на 0,021 млн. шт. в год или на 0,27%.

Задача 7. Имеются данные о численности задержанных правонарушителей на начало месяца.

Месяц	Численность работников на начало месяца чел.
	Вариант 5
Январь отчетного года	74
Февраль	79
Март	79
Апрель	91
Май	89
Июнь	79
Июль	86
Август	87
Сентябрь	89
Октябрь	97
Ноябрь	99
Декабрь	62
Январь следующего года	68

Необходимо рассчитать среднегодовую численность задержанных.

Решение.

Среднегодовую численность задержанных определяем по формуле средней хронологической:

84 чел.

Задача 8. Имеются данные о численности задержанных правонарушителей на определенные дни месяца.

Необходимо рассчитать среднегодовую численность задержанных, как средний уровень динамического ряда.

Решение.

В данном случае среднегодовую численность задержанных определяем по формуле:

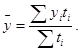
где ti - продолжительность периода между датами.

Получаем:

 чел.

Задача 9.Имеются данные о степени компьютеризации проведения криминалистических экспертиз за ряд лет.

Год	Уровень компьютеризации, %
	Вариант 5
1982	20,79
1983	19,32
1984	19,11
1985	19,11
1986	18,69
1987	16,59
1988	16,17
1989	16,17
1990	15,75
1991	14,91
1992	14,49
1993	12,39
1994	11,55
1995	11,34
1996	12,18
1997	12,39
1998	13,02
1999	14,07
2000	14,49
2001	15,75
2002	16,59
2003	18,06
2004	18,69
2005	18,69
2006	20,79

Необходимо

1.  Провести выравнивание динамического ряда при помощи

•  средней скользящей;

•  аналитического выравнивания динамического ряда, подобрав наиболее подходящую функцию графическим методом.

2.  Провести экстраполяцию на 2007 год.

Решение.

1. Проведем выравнивание динамического ряда при помощи средней скользящей (используем трехлетнюю среднюю скользящую). При этом уровни ряда заменяются по формулам:

 и т.д.

Результаты:

Таблица 9.1.

Год	yi	Скользящая средняя
1983	20,79
1984	19,32	19,74
1985	19,11	19,18
1986	19,11	18,97
1987	18,69	18,13
1988	16,59	17,15
1989	16,17	16,31
1990	16,17	16,03
1991	15,75	15,61
1992	14,91	15,05
1993	14,49	13,93
1994	12,39	12,81
1995	11,55	11,76
1996	11,34	11,69
1997	12,18	11,97
1998	12,39	12,53
1999	13,02	13,16
2000	14,07	13,86
2001	14,49	14,77
2002	15,75	15,61
2003	16,59	16,80
2004	18,06	17,78
2005	18,69	18,48
2006	18,69	19,39

Изобразим фактические данные:

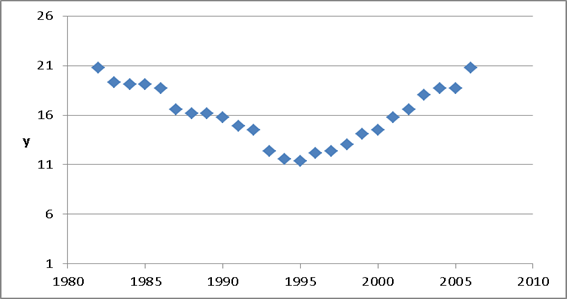
Рис. График фактических данных.

Мы видим, что функция имеет минимум, поэтому ищем уравнение тренда в виде:

Параметры уравнения вычисляем с помощью метода наименьших квадратов с системы:

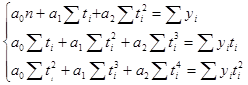
Вспомогательные данные:

Таблица 9.2.

	t	y	t^2	t^3	t^4	y*t	y*t^2	yteor
	1	20,79	1	1	1	20,79	20,79	22,0853
	2	19,32	4	8	16	38,64	77,28	20,7102
	3	19,11	9	27	81	57,33	171,99	19,4487
	4	19,11	16	64	256	76,44	305,76	18,3008
	5	18,69	25	125	625	93,45	467,25	17,2665
	6	16,59	36	216	1296	99,54	597,24	16,3458
	7	16,17	49	343	2401	113,19	792,33	15,5387
	8	16,17	64	512	4096	129,36	1034,88	14,8452
	9	15,75	81	729	6561	141,75	1275,75	14,2653
	10	14,91	100	1000	10000	149,1	1491	13,799
	11	14,49	121	1331	14641	159,39	1753,29	13,4463
	12	12,39	144	1728	20736	148,68	1784,16	13,2072
	13	11,55	169	2197	28561	150,15	1951,95	13,0817
	14	11,34	196	2744	38416	158,76	2222,64	13,0698
	15	12,18	225	3375	50625	182,7	2740,5	13,1715
	16	12,39	256	4096	65536	198,24	3171,84	13,3868
	17	13,02	289	4913	83521	221,34	3762,78	13,7157
	18	14,07	324	5832	104976	253,26	4558,68	14,1582
	19	14,49	361	6859	130321	275,31	5230,89	14,7143
	20	15,75	400	8000	160000	315	6300	15,384
	21	16,59	441	9261	194481	348,39	7316,19	16,1673
	22	18,06	484	10648	234256	397,32	8741,04	17,0642
	23	18,69	529	12167	279841	429,87	9887,01	18,0747
	24	18,69	576	13824	331776	448,56	10765,44	19,1988
	25	20,79	625	15625	390625	519,75	12993,75	20,4365
Сумма	325	401,1	5525	105625	2153645	5126,31	89414,43

Подставляем:

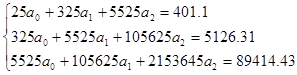
Ее решение:

a0 =	23,574
a1=	-1,5455
a2=	0,0568

Уравнение тренда:

2. Теоретические значения тренда рассчитаны в последнем столбике таблицы.

Прогноз на 2007 год:

t	ypr
2007	21,7878

Задача 10. Имеются данные о сдельной среднемесячной заработной плате за ряд лет тыс. руб.

Месяц	Вариант 7
	2004г	2005г	2006г
Январь	7,28	8,52	5,46
Февраль	7,54	9,12	5,88
Март	8,06	7,80	6,93
Апрель	6,76	7,44	4,62
Май	6,50	7,20	3,78
Июнь	6,11	6,72	3,99
Июль	4,16	6,12	3,32
Август	6,50	7,68	6,72
Сентябрь	8,19	7,80	6,72
Октябрь	8,97	7,80	7,77
Ноябрь	9,10	8,16	8,19
Декабрь	10,14	8,28	9,87

Необходимо провести анализ внутригодовой динамики изменения заработной платы, выявить сезонность данных изменений, предварительно проведя аналитическое выравнивание динамического ряда по прямой или по другой более подходящей функции.

Решение.

Проведем выравнивание по прямой:

Параметры уравнения вычисляем с помощью метода наименьших квадратов с системы:

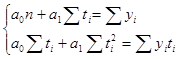
Вспомогательные данные:

Таблица 10.1.

	t	y	t^2	y*t	Ytteor	isez = yt/ytteor
	1	7,28	1	7,28	7,6366	0,9533
	2	7,54	4	15,08	7,6053	0,9914
	3	8,06	9	24,18	7,574	1,0642
	4	6,76	16	27,04	7,5427	0,8962
	5	6,5	25	32,5	7,5114	0,8654
	6	6,11	36	36,66	7,4801	0,8168
	7	4,16	49	29,12	7,4488	0,5585
	8	6,5	64	52	7,4175	0,8763
	9	8,19	81	73,71	7,3862	1,1088
	10	8,97	100	89,7	7,3549	1,2196
	11	9,1	121	100,1	7,3236	1,2426
	12	10,14	144	121,68	7,2923	1,3905
	13	8,52	169	110,76	7,261	1,1734
	14	9,12	196	127,68	7,2297	1,2615
	15	7,8	225	117	7,1984	1,0836
	16	7,44	256	119,04	7,1671	1,0381
	17	7,2	289	122,4	7,1358	1,0090
	18	6,72	324	120,96	7,1045	0,9459
	19	6,12	361	116,28	7,0732	0,8652
	20	7,68	400	153,6	7,0419	1,0906
	21	7,8	441	163,8	7,0106	1,1126
	22	7,8	484	171,6	6,9793	1,1176
	23	8,16	529	187,68	6,948	1,1744
	24	8,28	576	198,72	6,9167	1,1971
	25	5,46	625	136,5	6,8854	0,7930
	26	5,88	676	152,88	6,8541	0,8579
	27	6,93	729	187,11	6,8228	1,0157
	28	4,62	784	129,36	6,7915	0,6803
	29	3,78	841	109,62	6,7602	0,5592
	30	3,99	900	119,7	6,7289	0,5930
	31	3,32	961	102,92	6,6976	0,4957
	32	6,72	1024	215,04	6,6663	1,0081
	33	6,72	1089	221,76	6,635	1,0128
	34	7,77	1156	264,18	6,6037	1,1766
	35	8,19	1225	286,65	6,5724	1,2461
	36	9,87	1296	355,32	6,5411	1,5089
Сумма	666	255,2	16206	4599,61		35,99972

Подставляем:

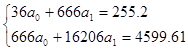
Ее решение:

а0 = 7,6679;

а1 = -0,0313

Уравнение линейного тренда:

Теоретические значения тренда рассчитаны в последнем столбике таблицы