Основы финансовых и коммерческих вычислений: Учебное пособие

Сумма дисконта по сложным процентным ставкам определяется по формуле:

Д = S - P = S - S (1 - d) ⁿ = S [ 1 - (1 - d) ⁿ ] .         (2.6)

В финансовых сделках при учете фактора инфляции сумму наращивания корректируют на величину, обратную индексу инфляции (если требуется определить реальную наращенную сумму в действующих ценах):

S’ = S * ()ⁿ ,                                  (2.7)

где   S’ - “реальная”, наращенная сумма с учетом инфляции;

k - темп инфляции.

Объединив формулы 2.6 и 2.7, получим выражение:

S’ = P * .                                         (2.8)

Формула 2.8 описывает два процесса: один - наращение суммы, другой - ее обесценивание.

S’ составляет будущую наращенную сумму в действующих ценах.

Например: Следует рассчитать реальную наращенную в течение пяти лет сумму долга с учетом инфляции при процентной ставке            5%   годовых  и  предполагаемого  годового  уровня  инфляции,      равного 5,5%. Размер кредита равен   5000  усл.ден.ед. В   данном     случае наращенная      сумма     долга будет     равна       S’    = 5000*

5

        [ (1+0,05)/(1+0,055)] = 4882,6 ден.ед. То есть реально наращенная сумма с учетом инфляции меньше первоначального долга.

Анализ формулы 2.8 с точки зрения учета влияния изменения конъюнктуры процентных ставок и динамики инфляции позволяет сделать следующие выводы:

1)  если  i = k то наращение равно нулю;

2)  если i > k , то первоначальная сумма возрастает на коэффициент превышения, равный  w = (1+i)/(1+k);

3)  если i < k , то первоначальная сумма уменьшится на коэффициент      w = (1+i)/(1+k). Такое конъюнктурное сочетание называется “эрозией” капитала.

S’’ = P *[(1+k)/(1+i)].                                         (2.9)

S’’- наращенная сумма в предполагаемых ценах (скорректированная на уровень инфляции).

2.3.Операции с использованием сложных процентов

Гораздо чаще, чем в случае с простыми процентами, при расчетах сложных процентов, возникают задачи определения сроков и уровня доходности финансовых операций. Кроме того, сочетание этих двух факторов на долгосрочном периоде делает  доходность  вероятностной величиной. Зависимость «доходность-срок операции» принято называть кривой доходности.

Расчет срока платежа при постоянных условиях взаиморасчета производится по следующей формулам:

n=log(S/P)/log(1+i);                                                                        (2.10)

n= log(S/P)/log(1-d).                                                                       (2.11)

d=1-(P/S)    .                                                                                     (2.13)

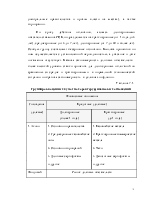
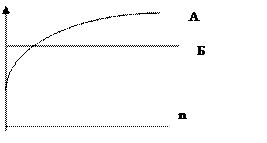
На графике кривой доходности (рис. 2.1) по оси ординат размещается шкала доходности (Y), по оси абсцисс – срок (n).

	Y
				Рис.2.1.Кривая  доходности

Кривая доходности характеризует изменение доходности конкретных кредитных операций или финансовых инструментов в зависимости от сроков. Изменение конъюнктуры меняет форму кривой и ее положение на графике. При стабильной конъюнктуре кривая доходности имеет форму кривой А (рис. 2.1).Доходность растет с замедлением по мере увеличения срока инвестиций. Такую кривую принято называть положительной кривой доходности. Кривая доходности близкая к горизонтальной прямой (Б на рис.2.1) указывает на то, что инвесторы не учитывая уровня риска сводят на нет доходность сделки.

3.Конверсия платежей

3.1.Финансовая эквивалентность платежей

В практике финансовых расчетов часто возникают случаи необходимости замены одних обязательств другими, равноценными условиями. Равноценными могут считаться такие условия, которые будучи