Другие предметы \ Метрология, стандартизация и сертификация

Диаграмма разброса. Диаграмма Парето

Страницы работы

15 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Контрольная работа

«Диаграмма разброса. Диаграмма Парето»

1. Диаграмма разброса

Диаграмма разброса (рассеивания) – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих факторов и выдвинуть гипотезу о наличии или отсутствии корреляционной связи между двумя случайными величинами. Она полезна в случае, когда между исследуемыми факторами не существует формализованной зависимости, но предполагается возможность вероятностной связи, силу которой в общем случае можно оценить по величине коэффициента корреляции. При наличии корреляционной зависимости можно осуществить контроль одной из двух характеристик, что позволит сократить время и стоимость процесса. При этом характер корреляционной зависимости, который определяется видом диаграммы разброса, дает представление о том, каким изменениям будет подвержен один из параметров при определенных изменениях другого.

Методика построения диаграммы разброса

Собрать парные данные (X, Y), между которыми необходимо исследовать зависимость, используя контрольный листок.

Расположить данные по одной их переменных в ранжированном порядке.

Построить на плоскости систему координат Х0Y; шкалы на горизонтальной и вертикальной осях подобрать таким образом, чтобы обе длины рабочих частей получились примерно одинаковыми, а оси имели от 5 до 10 градаций и имели круглые числа.

Отложить значения каждой пары данных на координатной плоскости точкой с координатами (X, Y); если в разных наблюдениях получаются одинаковые значения, показать эти точки, рисуя концентрические кружки.

Сделать все необходимые обозначения: название диаграммы, число пар данных, названия и единицы измерения для каждой оси, данные о составителе диаграммы.

Анализ диаграммы

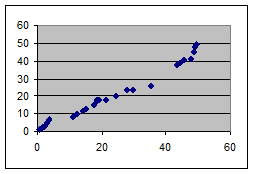
В наличии или отсутствии связи между параметрами можно убедиться визуально, по виду расположения точек на диаграмме. Так, при увеличении Х (рис. 1) Y также будет увеличиваться (прямая корреляция). В этом случае при осуществлении контроля над фактором X характеристика Y будет оставаться стабильной.

Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.

а) б)

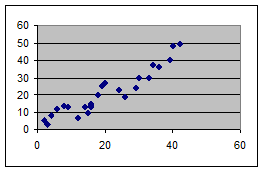
Рисунок 1 – Прямо пропорциональная связь (положительная)

а) б)

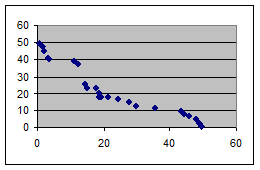
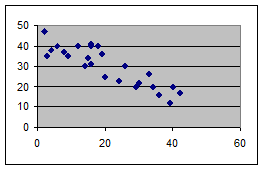
Рисунок 2 – Обратно пропорциональная связь (отрицательная)

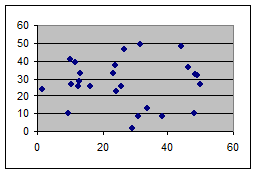
Рисунок 3 – Корреляционная связь отсутствует

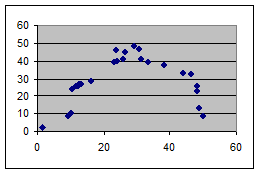
Рисунок 4 – Корреляционная связь нелинейная

На рис. 1а и 2а точки расположены более тесно к гипотетической прямой линии, чем на рис. 1б и 2б, поэтому можно говорить о более сильной корреляционной связи.

На рис. 2 показан пример обратной (отрицательной) корреляции. При увеличении X значения Y уменьшаются. Если фактор X находится под контролем, характеристика Y остается стабильной.

На рис. 3 показан пример отсутствия корреляции, когда никакой выраженной зависимости между Х и Y не наблюдается. В этом случае необходимо продолжить поиск факторов, коррелирующих с Y, исключив из этого поиска фактор X.

Между параметрами Х и Y возможны также случаи нелинейной корреляции (рис. 4). При этом диаграмму разброса можно разделить на более мелкие участки и исследовать каждый из них в отдельности.

Выполнение работы

Таблица 1 – исходные данные.

xi -процент легирующих добавок в сплаве ×10-2, yi - относительное удлинение ×10-3

№ П/п	Xi	Yi	№ п/п	Xi	Yi	№ п/п	Xi	Yi
1	114	16	11	135	30	21	175	41
2	116	17	12	143	31	22	177	42
3	119	18	13	144	32	23	178	44
4	119	20	14	149	33	24	183	45
5	121	20	15	152	33	25	189	46
6	122	21	16	159	34	26	190	46
7	124	22	17	164	34	27	195	48
8	130	23	18	165	37	28	196	49
9	131	23	19	172	37	29	197	51
10	133	24	20	173	38	30	197	54

P=0,95 ; Xr=1,96.

Парные данные упорядочены по х.

Определяем средние значения и стандартные отклонения факторов:

; ;

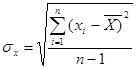= 28,51; 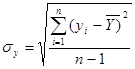= 11,309.

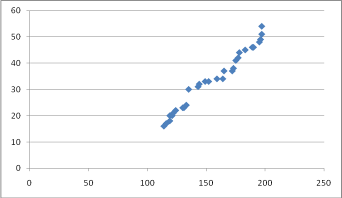
Рисунок 5 – «Диаграмма разброса».

Прямо пропорциональная связь (положительная).

Количественная оценка силы связи между исследуемыми факторами определяется посредством коэффициента корреляции r по формуле:

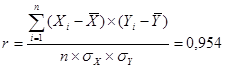(1)

где: n – число пар значений исследуемых факторов;

, , sX, sY – средние значения и среднеквадратические отклонения соответственно входного и выходного факторов.

Если значение r близко к ±1, можно предположить наличие корреляционной зависимости близкой к функциональной. Если - 0,3 < r < 0,3, можно предположить, что линейная корреляционная связь отсутствует, либо она существенно не линейная.

Чем ближе коэффициент корреляции к единице, тем теснее зависимость между параметрами. Принято считать, что:

при r = |0,3| – слабая связь, при r = |0,3…0,7| – средняя связь, при r = |0,7…0,9| - сильная связь, при r ³ |0,9| – весьма сильная связь.

Проверка значимости коэффициента корреляции

Коэффициент корреляции r, определенный по выборочным данным, может не совпадать с действительным значением, соответствующим генеральной совокупности, поэтому следует оценить степень доверия, с которой он может быть использован при переносе на неё.

Ошибка выборочного коэффициента парной корреляции определяется как стандартное отклонение:

(3)