Решение задач по финансовой математике (Определение величины процентных денег при расчете их по обыкновенному (банковскому) варианту. Определение величины выплаты задолженности)

Решение задач по финансовой математике.

Задание 1.6

За время пользования долгом величина процентных денег составила 25000 д.е. при временной базе 365 дней. Найти величину процентных денег при расчете их по обыкновенному (банковскому) варианту при тех же остальных условиях начисления простых процентов.

Решение.

Величина процентных денег при временной базе 365 дней:

25000 = (S₀ ∙ n ∙ i) / 365,

Где n – число дней в периоде пользования,  S₀ -  начальная сумма вклада, i- годовая процентная ставка. Откуда:

S₀ ∙ n ∙ i  = 25000 ∙ 365

Величина процентных денег при временной базе 360 дней:

(S₀ ∙ n ∙ i) / 360 = (25000 ∙ 365)/360 = 25350 д.е.

Задание 2.9

На ссуду 10000 д.е. начисляются сложные проценты в конце каждого квартала по годовой номинальной процентной ставке 0,05. Определите величину долга через 5 и 10 лет.

Решение.

Воспользуемся формулой сложных процентов:

,

Где S – наращенная сумма ссуды, P – начальная сумма ссуды, j – годовая процентная ставка, m – число раз в году начисления процентов, n – число лет в периоде.

Определим величину долга через 5 лет:

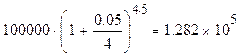
Величина долга через 5 лет составит 12820 д.е.

Определим величину долга через 10 лет:

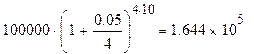
Величина долга через 10 лет составит 16440 д.е.

Задание 3.12

Две фирмы имеют годовые обороты 1 млн д.е. и 2 млн д.е. соответственно. Оборот первой фирмы растет ежемесячно на 2 %, а оборот второй - уменьшается на 1 %. Определите, когда годовые обороты фирм станут одинаковыми.

Решение.

Для решения задачи воспользуемся формулой сложных процентов:

,

Где j  - месячная процентная ставка, m – число месяцев.

На основании приведенной выше формулы составляем уравнение:

Решая полученное уравнение, определяем, когда годовые обороты фирм будут одинаковыми.

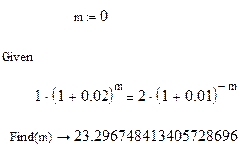
Примерно через 23 месяца годовые обороты фирм будут одинаковыми.

Задание 4.15

На начальную сумму ссуды предусматривается непрерывное начисление процентов по силе роста, изменяющейся дискретно по следующей схеме; первые два года она равна 0,08, следующие три года— 0,09 и далее в течение 5 лет- 0,1. Определите множитель на ращения и эквивалентную годовую процентную ставку при начислении сложных процентов.

Решение.

Воспользуемся формулой:

,

Где d_i – сила роста в i-ый промежуток времени, t_i – продолжительность i-го промежутка времени.

Находим множитель наращения:

Множитель наращения составляет 2,535.

Определяем эквивалентную процентную годовую ставку при начислении сложных процентов по формуле:

,

Где n – число лет, к – множитель наращения.

Эквивалентная годовая ставка сложных процентов составляет 9,7%.

Задание 5.18

Между январем 1990 г и январем 1994 г. индекс потребительских цен I_Р (уровень инфляции) вырос со 121 до 636. Определите годовой темп прироста цен за этот период в процентах. Выразите индекс цен в форме а∙е^k∙t, если величина индекса цен при t=0 соответствует индексу цен в январе 1990 г. Предполагая темп прироста индекса цен постоянным, установите, когда индекс цен достигнет величины 5000?

Решение.

Определим среднегодовой темп роста цен по формуле:

,

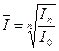Где n – число лет, I₀ – значение индекса инфляции в момент, принятый за базу сравнения, I_n – значения индекса инфляции в n-ый период времени.

Находим:

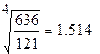
Ежегодно с 1990 года по 1994 год индекс инфляции в среднем возрастал на 51,4%.

Выразим индекс цен в форме а∙е^k∙t. При t=0, a = I₀ = 121

,

Откуда находим k:

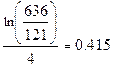
В результате получим:

Определим период времени, когда величина индекса цен достигнет 5000:

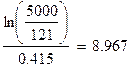
Через 9 лет величина индекса цен достигнет 5000.

Задание 6.1

Создается страховой фонд. В конце каждого года делается взнос в размере 40000 д.е. и на собранные деньги начисляются сложные проценты по годовой процентной ставке 0,1. Выведите формулу наращенной суммы через n лет. Определите размер фонда через 10 лет.

Решение.

Выведем формулу наращенной суммы. Пусть R – величина годового взноса, i- годовая процентная ставка, n – число лет, тогда величина наращенной суммы:

S = R∙(1+i)ⁿ + R∙(1 + i)^n-1 + R∙(1 + i)^n-2 + R∙(1 + i)^n-3 +  … + R.

Мы получили геометрическую прогрессию с первым членом a₁ = R  и знаменателем

q = (1 + i).

Сумма членов геометрической прогрессии:

Найдем размер фонда через 10 лет:

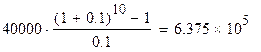
Размер фонда составит 637500 д.е.

Задание 7.4

Чтобы   через   10  лет  приобрести   оборудование   по   цене 120000 д.е., фирма планирует создать резервный фонд. Сумма ежеквартальных взносов, которые депонируются под сложные проценты, начисляемые каждый квартал по годовой процентной ставке 0,08, равна 1986,69 д.е. После 34-го взноса (8,5 лет) годовая процентная ставка увеличилась до 0,12. Определите величину квартальных взносов в оставшийся период