Моделирование тепловых характеристик интегральных схем в импульсном режиме работы: Методические указания к лабораторной работе по курсу «Теплофизическое проектирование РЭС»

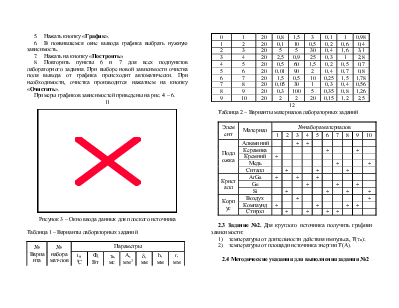
Формула (8) позволяет оценить условия, при которых можно использовать понятие полупространства и полученные для рассмотренной модели зависимости (5). Пусть, например, область с источником расположена на поверхности тела конечной толщины

7

h (рис. 1, а); если выполняется неравенство

                                 (9)

то данное тело можно считать полупространством.

В практических задачах источник занимает, как правило, ограниченную область и возникает вопрос о правомерности применения формул (5) и (9) для расчета температурного поля. Например, источник расположен в прямоугольнике со сторонами 2l₁, 2l₂, причем l₁£l₂. Рассмотрим отношение наименьшего размера источника к толщине прогретого слоя:

                                                    (10)

Если N>>1, то прогретый слой значительно меньше l₁, т. е. почти  весь  поток направлен в глубь полупространства в направлении оси x и рассмотренная модель правомерна, в противном случае этой моделью пользоваться нельзя.

Круглый источник. Перейдем  ко второй модели – на адиабатной поверхности полупространства тепловой поток вырабатывается в области И, имеющей форму круга радиусом r. Математическая модель представляет собой систему уравнений (1) – (4) с условием /3/

                          (11)

на границе x=0, в котором при описании области И следует учесть, что последняя имеет форму круга. Решение этой задачи приведено в /3/; для центра источника (x=y=z=0) выражение для температуры имеет вид

         (12)

где

8

1.2 Микросхемы с импульсными источниками

Модель микросхемы. Пусть элемент 3 расположен на некоторой плате 2 и окружен слоем материала 1 (рисунок 2).

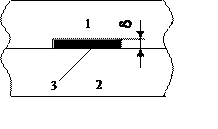Рисунок 2 – Модель микросхемы;

Вся поверхность элемента  является  источником теплоты и в течение времени t_и действия импульса рассеивает поток Ф.

Будем считать, что скважность импульсов велика и за время между импульсами температура элемента успевает возвращаться к исходному состоянию. Определим среднюю температуру t_э элемента, полагая, что его температурное поле равномерно.

Рассеиваемый источником поток Ф частично переходит в область 1Ф₁ и 2Ф₂, а частично аккумулируется в элементе 3Ф₃ и повышает его температуру, т. е. Ф=Ф₁+Ф₂+Ф₃; Ф₃=с_р3r₃V₃du_э/dt, где с_р3, r₃, V₃ – удельная теплоемкость, плотность и объем области 3. В первом приближении можно предположить, что температура в области 3 изменяется за время t_и по линейному закону, т. е. du_э/dt»u_t/t_и, тогда

                          Ф=Ф₁+Ф₂+с_р3r₃V₃u_э/t_и,  V₃=Ad.                     (13)

Найдем Ф₁ и Ф₂ с помощью выражений (6), (11) и (1.123, 1.124, /1/) в зависимости от формы источника, площадь которого обозначим А, а толщину d.

Плоский источник. Из (6) находим:

9

где l_i, a_i – теплопроводность и температуропроводность областей i=1, 2.

Подставим значения Ф₁ и Ф₂ в (12) и найдем температуру:

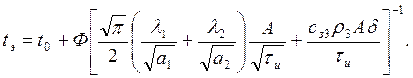                   (14)                                  

Если свойства областей 1 и 2 одинаковы (l_i=l, a_i=a), то формула (13) становится проще:

                                         (15)

Первый член в скобках формулы (14) учитывает потоки Ф₁ и Ф₂, а второй – Ф₃; полагая первый член на порядок больше, чем второй:  найдем выражение для длительности импульса t_и^*, при которой можно пренебречь аккумуляцией теплоты в элементе 3:

                                                 t_и^*³32d²/а.                                       (16)

Напомним, что полученные зависимости (14) и (15) справедливы, если выполняются условия (9) и (10).

Источник энергии в форме круга радиусом r. Аналогично можно найти зависимость для максимальной температуры (t_э)_max, если источник имеет форму круга; для этого необходимо воспользоваться уравнениями (11) и (12), в последнем пренебрегаем аккумуляцией теплоты (с_р3=0):

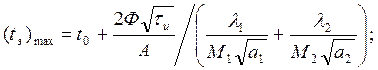                          (16)

10

2 ЛАБОРАТОРНЫЕ ЗАДАНИЯ

2.1 Задание №1. Для плоского источника получить графики зависимости:

1)  температуры от длительности действия импульса, Т(t_и);

2)  температуры от рассеиваемого потока, Т(Ф);

3)  толщины прогретого слоя от длительности действия импульса, x^*(t_и).

2.2 Методические указания для выполнения задания №1

1.  Запустить программу путем открытия файла «Микросхемы с импульсными источниками.exe».

2.  В появившемся окне меню-заставки выбрать «Плоский источник».

3.  Для продолжения нажать кнопку «ОК», для выхода из программы нажать кнопку «Выход».

4.  В появившемся окне для ввода данных (рис. 3) согласно варианту необходимо:

а) выбрать материалы: подложки, кристалла и корпуса;

б) последовательно ввести все остальные параметры.

Варианты лабораторных заданий выбираются из табл. 1 и 2 согласно последней цифре номера зачетной книжки.

5.  Нажать кнопку «График».

6.  В появившемся окне вывода графика выбрать нужную зависимость.

7.  Нажать на кнопку «Построить».

8.  Повторить пункты 6 и 7 для всех подпунктов лабораторного задания. При выборе новой зависимости очистка поля вывода от графика происходит автоматически. При необходимости, очистка производится нажатием на кнопку