








































Квантовая теория
![]()
![]()
![]()
Семестр II
Тема
Лекция XVIII
Теория рассеяния в приближении Борна
Как наблюдать взаимодействие квантовых частиц?
![]()
Измерительные характеристики
![]()
Что измеряют при исследовании рассеяния?
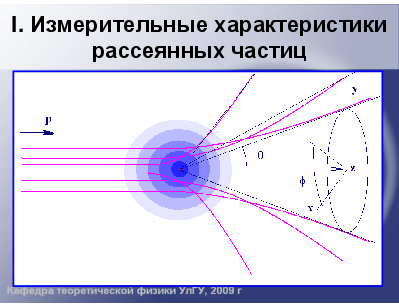
I. Измерительные характеристики рассеянных частиц
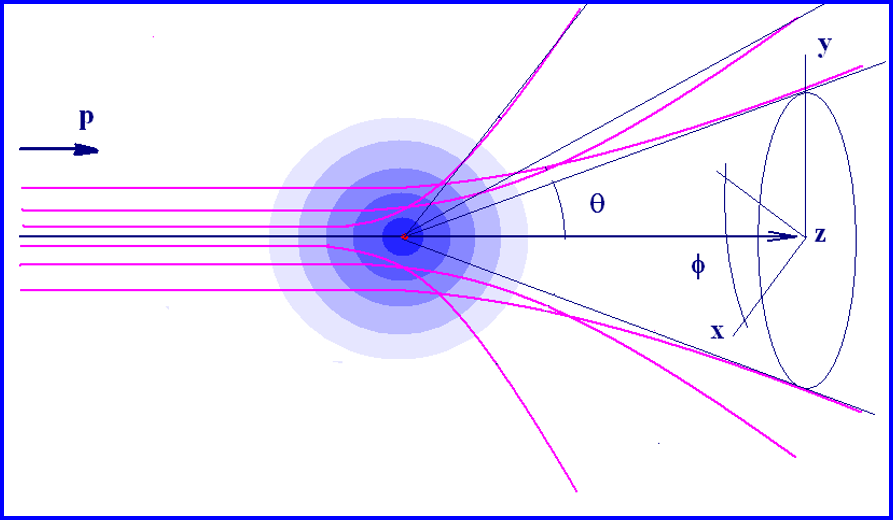
I. Измерительные характеристики рассеянных частиц
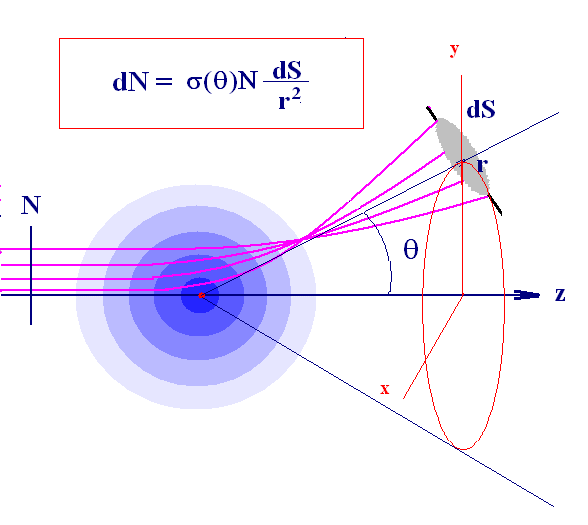
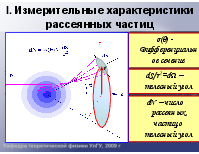
σ(θ) - Дифференциальное сечение
r
dS/r2=dΩ – телесный угол
dN – число рассеяных частиц в телесный угол
I. Измерительные характеристики рассеянных частиц
Число частиц на единицу пути в веществе, выбывших из потока, за счет рассеяния
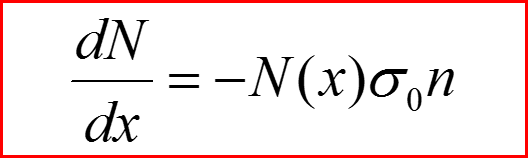
n – концентрация рассеивающих частиц , σ0 – полное сечение
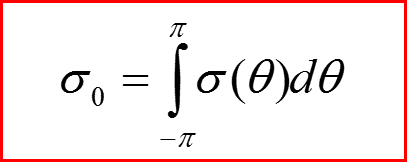
I. Измерительные характеристики рассеянных частиц
Вероятность пройти путь x без рассеяния равна:
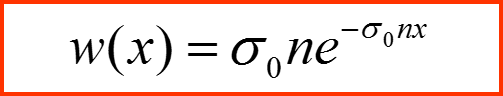
Средняя длина свободного пробега Λ равна:
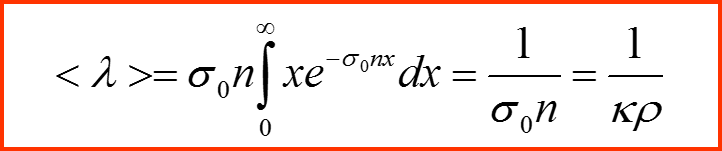
Квантовая задача рассеяния
![]()
Чем отличаются классическая и квантовая теории рассеяния?
II. Квантовая задача рассеяния
Предполагаем, что источник рассеиваемых частиц создает стационарный поток частиц. Поэтому уравнение для волновой функции частиц в потоке будет иметь вид стационарного уравнения Шредингера:
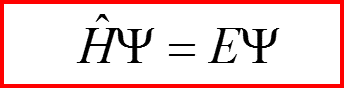
II. Квантовая задача рассеяния
Будем полагать, что рассеивающий потенциал – обладает центральной симметрией:
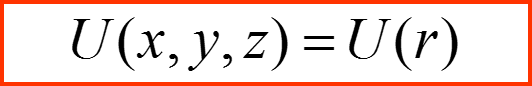
II. Квантовая задача рассеяния
Задача рассеяния – это задача о движении частиц вне потенциальной ямы
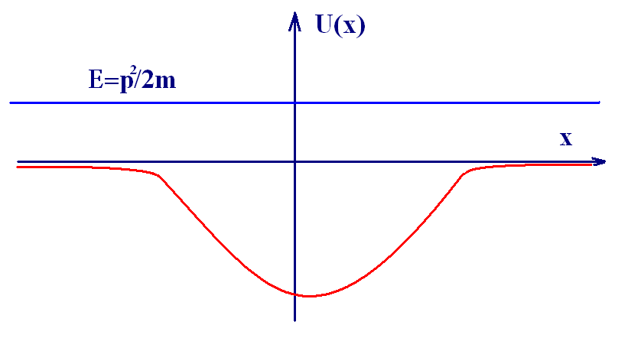
II. Квантовая задача рассеяния
Уравнение Шредингера для непрерывного спектра
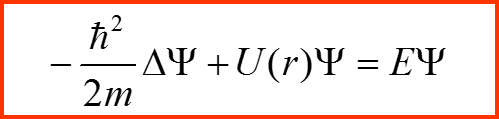
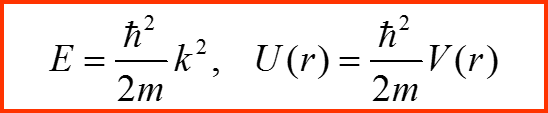
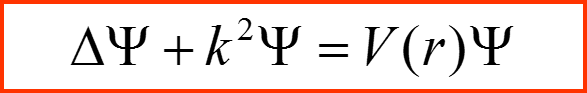
II. Квантовая задача рассеяния
Волновая функция частицы:
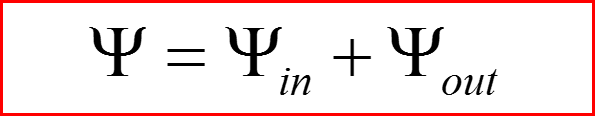
Ψin - волновая функция падающей частицы.
Ψout - волновая функция рассеянной частицы.
II. Квантовая задача рассеяния
Граничные условия для падающей волны:

До рассеяния состояние частицы описывается волновой функцией Де Бройля.
II. Квантовая задача рассеяния
Граничные условия для рассеянной волны:
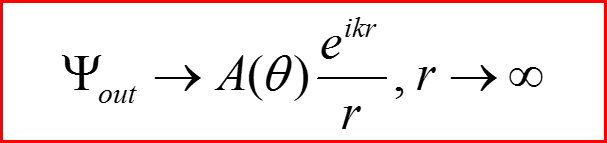
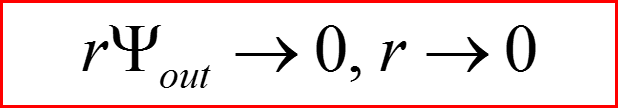
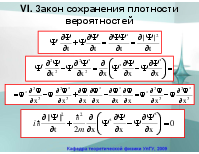
VI. Закон сохранения плотности вероятностей
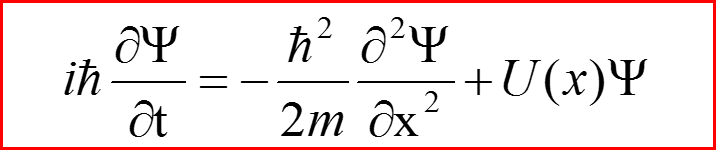
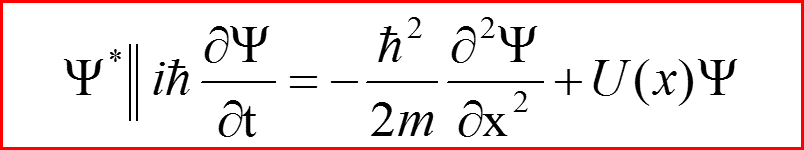
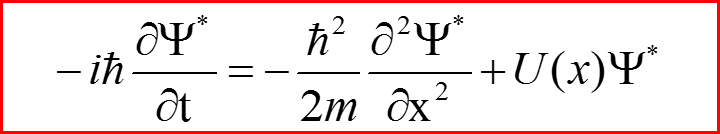
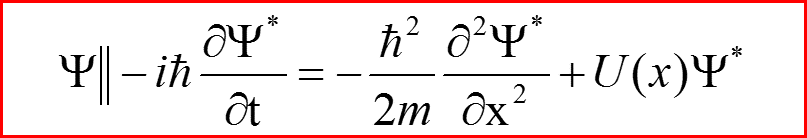
![]()
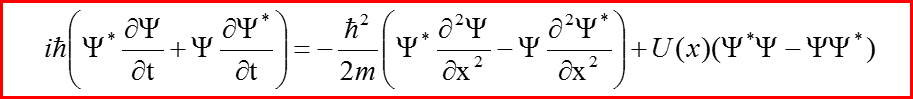
VI. Закон сохранения плотности вероятностей
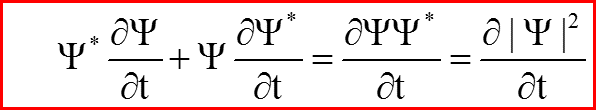
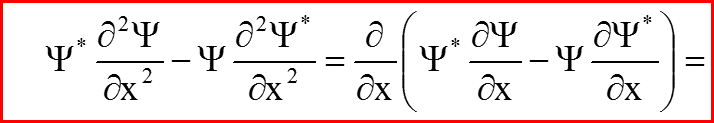
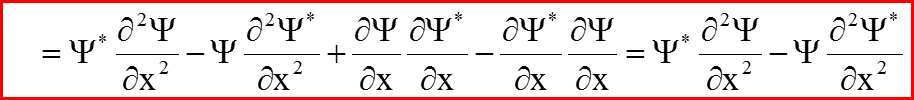
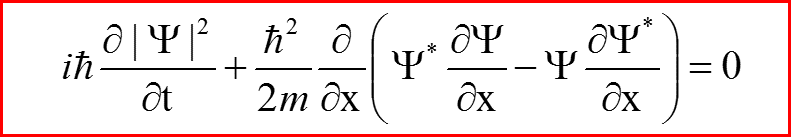
VI. Закон сохранения плотности вероятностей
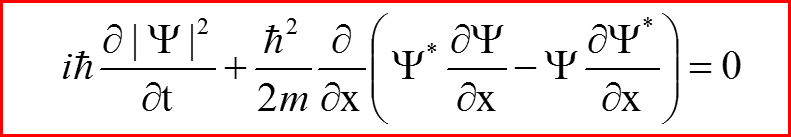
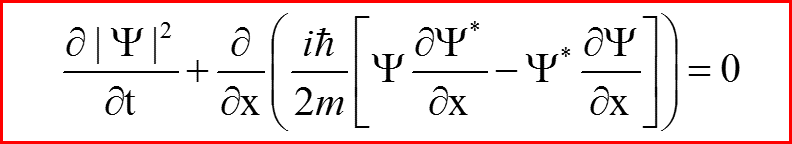
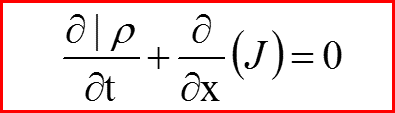
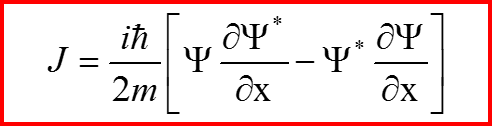
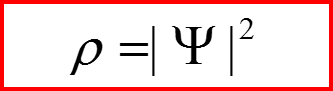
VI. Закон сохранения плотности вероятностей
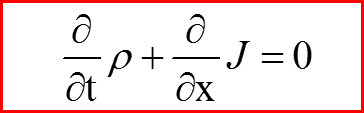
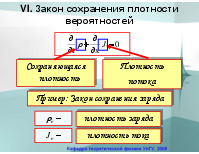
Плотность потока
Сохраняющаяся плотность
Пример: Закон сохранения заряда
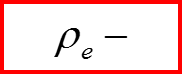
плот ность заряда
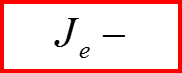
плотность тока
VI. Закон сохранения плотности вероятностей
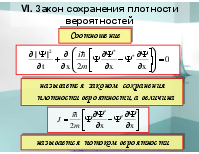
Соотношение
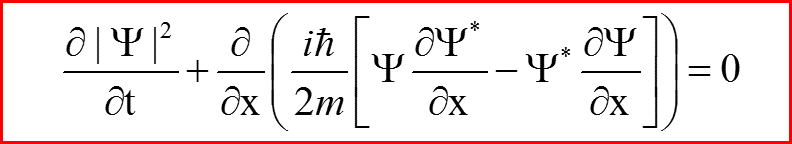
называется законом сохранения плотности вероятности, а величина
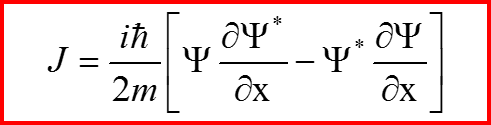
называется потоком вероятности
VI. Дифференциальный закон сохранения
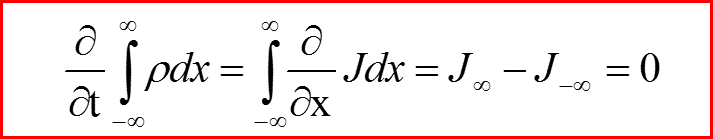
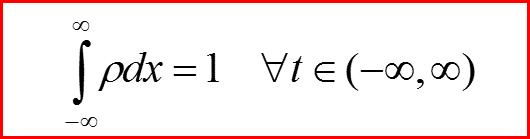
Нормировка плотности вероятности сохраняется!
II. Квантовая задача рассеяния
Нормировка волновой функции падающей частицы
Число частиц на 1 см2 в 1 с равно N=Jz
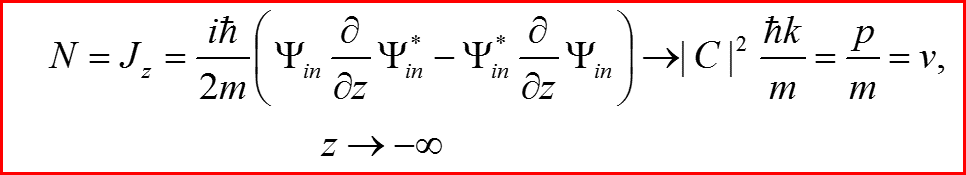
II. Квантовая задача рассеяния
Нормировка волновой функции рассеянной частицы.
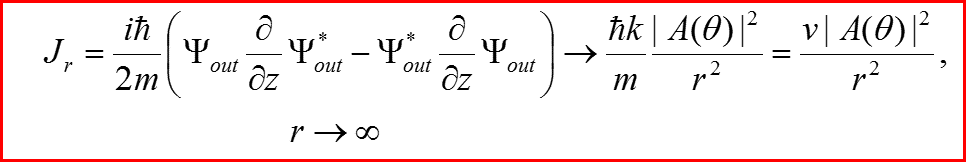
II. Квантовая задача рассеяния
Связь дифференциального сечения σ(θ) с амплитудой рассеяния A(θ)
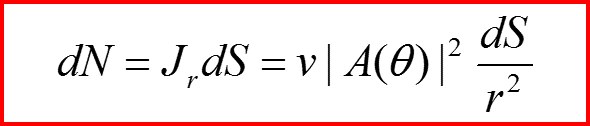
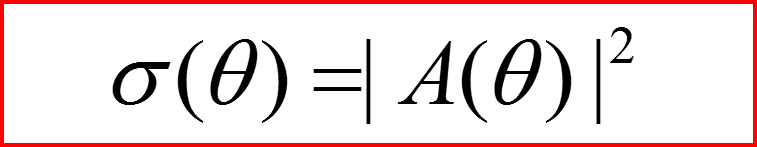
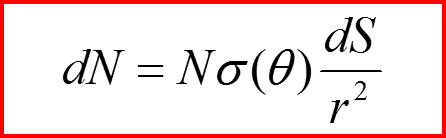
Поскольку при выбранной нормировке V=N!!!
III. Приближение Борна
Приближение Борна является одной из форм теории возмущения!
Малым параметром Λ в приближении Борна является отношение потенциальной энергии налетающей частицы к ее кинетической энергии:
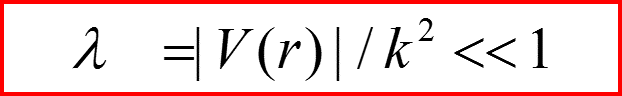
III. Приближение Борна
В этом случае уравнение Шредингера можно записать в таком виде:
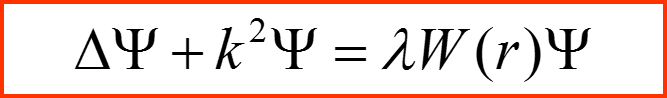
III. Приближение Борна
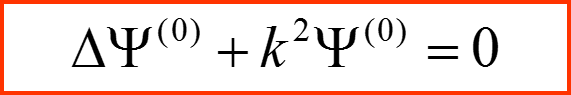
0
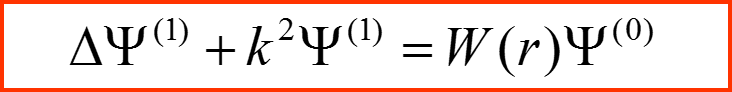
1
2
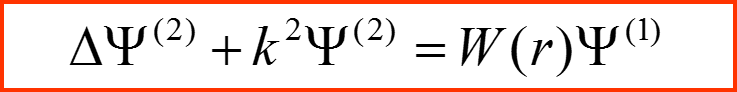
III. Приближение Борна

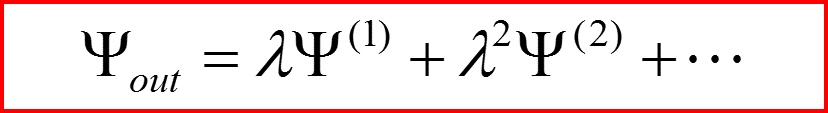
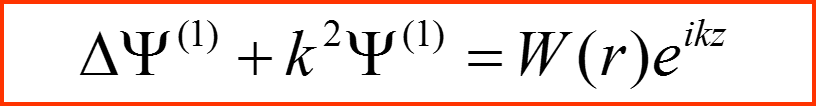
III. Приближение Борна
Уравнение
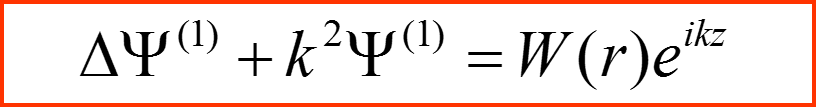
По форме является уравнением
ГЕЛЬМГОЛЬЦА!!!
III. Приближение Борна
Уравнение Гельмгольца
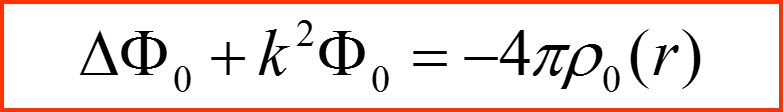
Является следствием
Волнового уравнения для потенциала электрического поля:
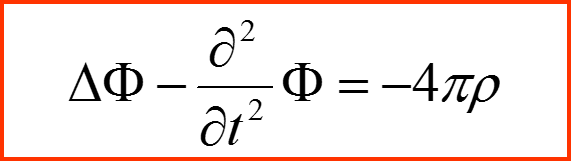
III. Приближение Борна
Решение уравнения Гельмгольца Ф0(r) Связано с решением волнового уравнения Ф(r,t) cоотношением:
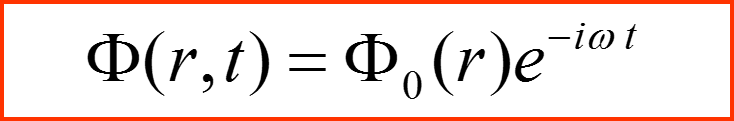
III. Приближение Борна
Волновое уравнение
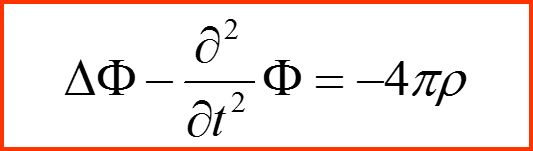
Имеет решение в виде запаздывающего потенциала:
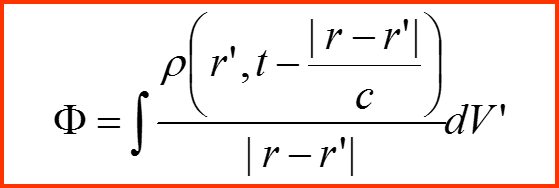
III. Приближение Борна
Сравнивая уравнение для Ψ(1) с уравнением Гельмгольца находим:
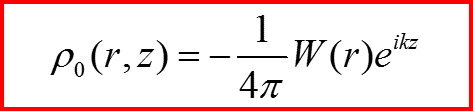
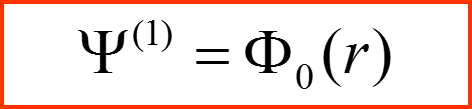
Положим
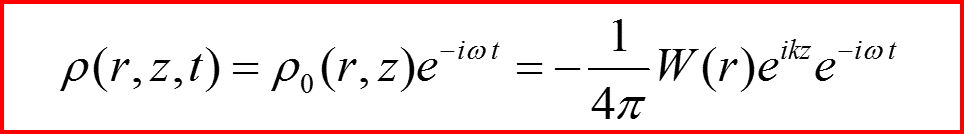
III. Приближение Борна
В результате получаем соотношение:
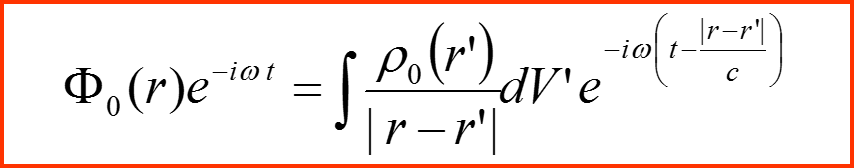
Отсюда:
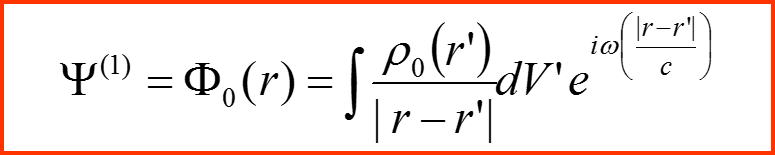
III. Приближение Борна
Тогда получаем решение в приближении Борна:
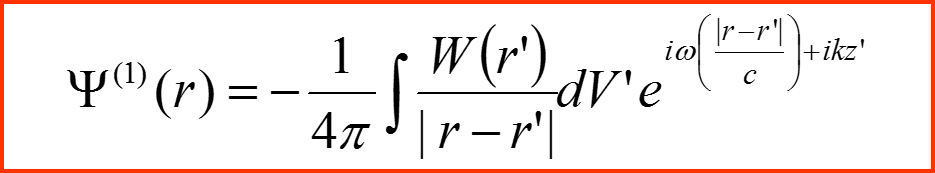
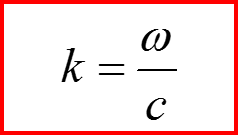
Вычисление амплитуды рассеяния
![]()
Асимптотика на бесконечности
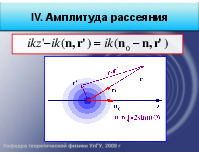
IV. Амплитуда рассеяния
В полученном решении необходимо перейти к пределу r→∞.
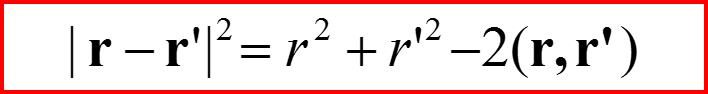
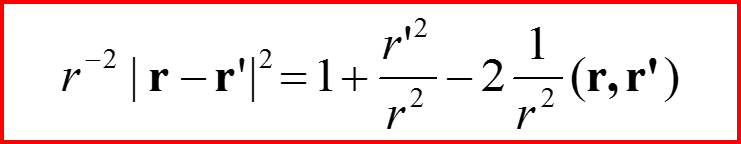
IV. Амплитуда рассеяния
При r’/r→0, r→∞
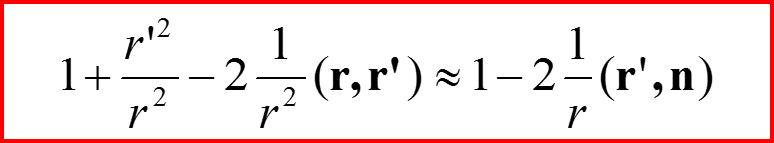
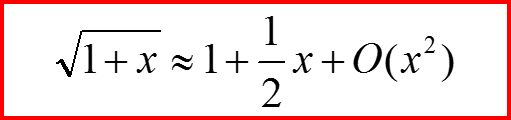
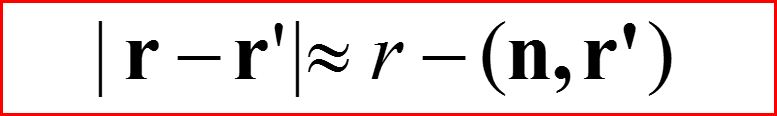
IV. Амплитуда рассеяния
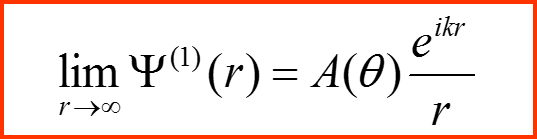
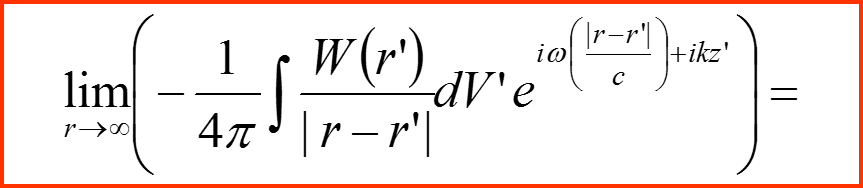
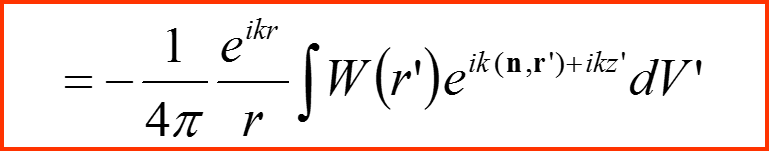
IV. Амплитуда рассеяния
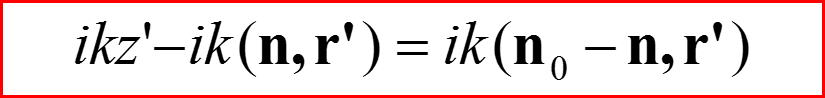
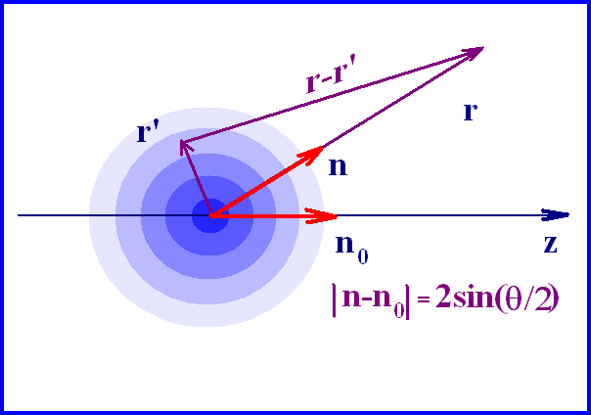
IV. Амплитуда рассеяния
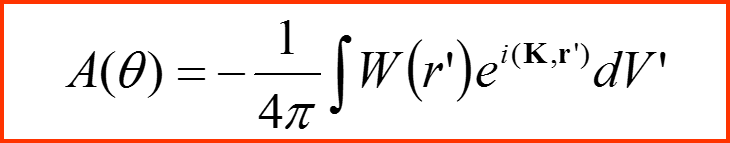
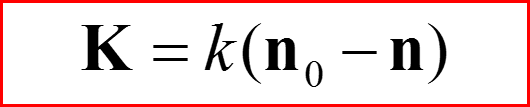
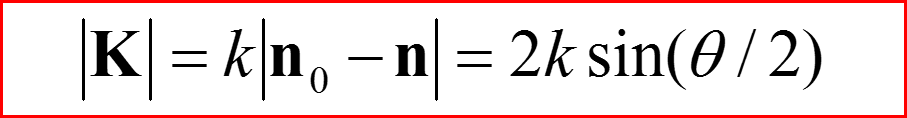
IV. Амплитуда рассеяния
Дифференциальное сечение рассеяния
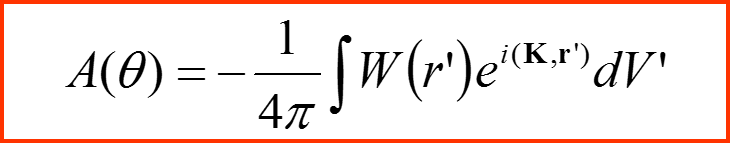
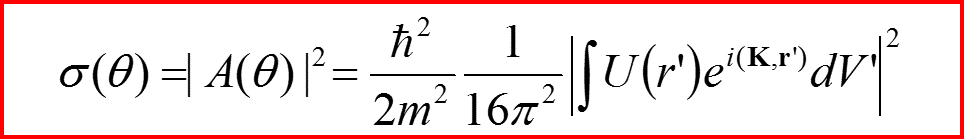
Упругое рассеяние на атомах
![]()
Формфактор
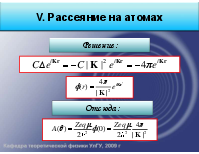
V. Рассеяние на атомах
Потенциал рассеяния на атоме с центрально-симметричным полем
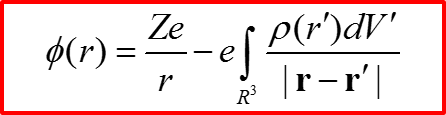
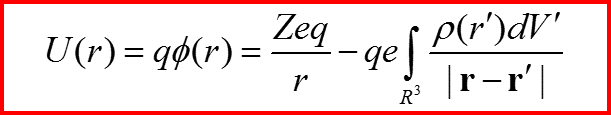
V. Рассеяние на атомах
Потенциал рассеяния на атоме с центрально-симметричным полем
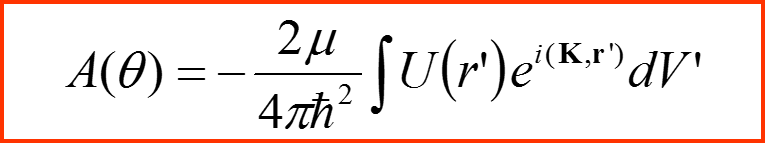
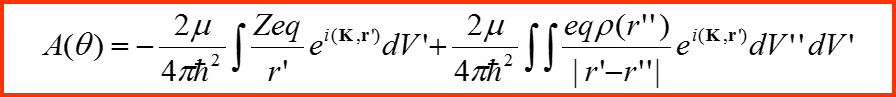
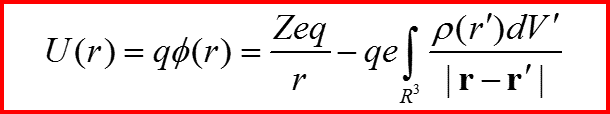
V. Рассеяние на атомах
Рассеяние на кулоновском потенциале
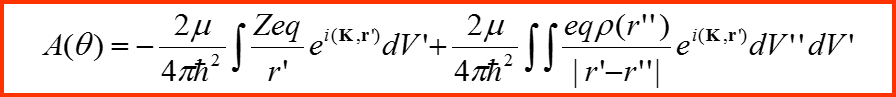
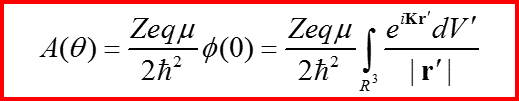
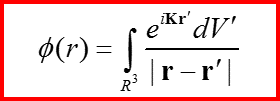

Ищем решение в виде:

V. Рассеяние на атомах
Решение:

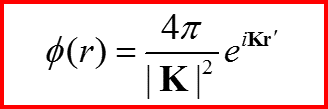
Отсюда:
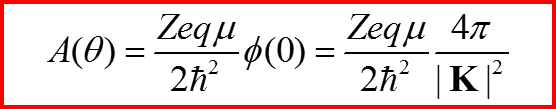
V. Рассеяние на атомах
Отсюда:
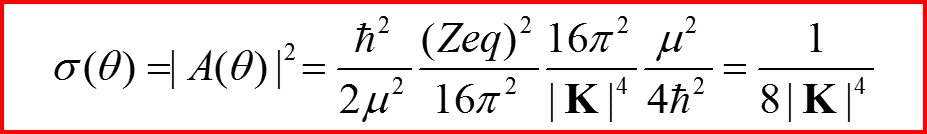
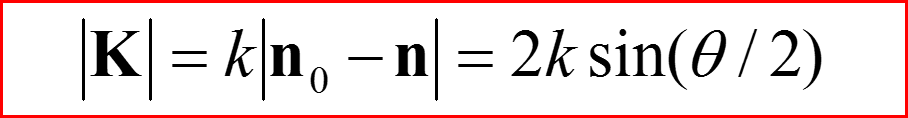
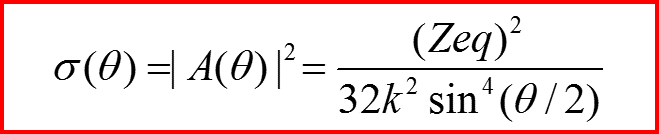
V. Рассеяние на атомах
Формфактор
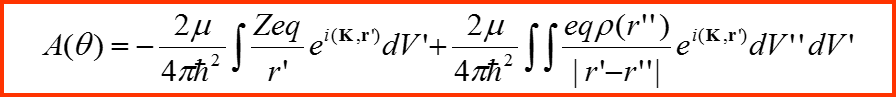
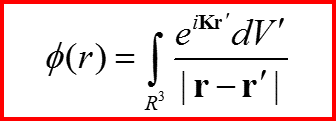
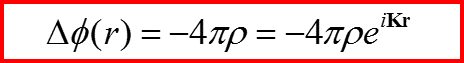
Ищем решение в виде:

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.