Уравнения по законам Кирхгофа. Определение токов в ветвях схемы методом контурных токов

Схема

 

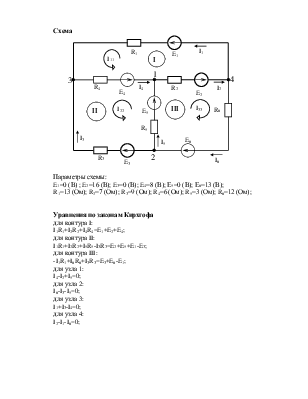
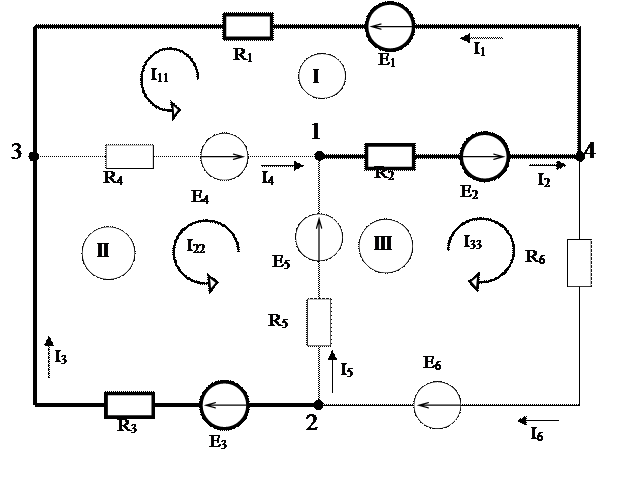
Параметры схемы:

E₁=0 (В) ; E₂=16 (В); E₃=0 (В); E₄=8 (В); E₅=0 (В); E₆=13 (В);

R₁=13 (Ом); R₂=7 (Ом); R₃=9 (Ом); R₄=6 (Ом); R₅=3 (Ом); R₆=12 (Ом);

Уравнения по законам Кирхгофа

для контура I:

I₁R₁+I₂R₂+I₄R₄=E₁+E₂+E₄;

для контура II:

I₁R₁+I₂R₂+I₅R₅-I₃R₃=E₂+E₅+E₁-E₃;

для контура III:

-I₁R₁+I₆R₆+I₃R₃=E₃+E₆-E₁;

для узла 1:

I₄-I₂+I₅=0;

для узла 2:

I₆-I₃-I₅=0;

для узла 3:

I₁+I₃-I₄=0;

для узла 4:

I₂-I₁-I₆=0;

Определение токов во всех ветвях схемы методом контурных токов

Пусть в контуре I течёт ток I₁₁; в контуре II ток I₂₂; в контуре III течёт ток I₃₃.

Система уравнений по методу контурных токов:

 

I₁₁(R₁+R₂+R₄)+I₂₂(R₂+R₁)-I₃₃R₁=-E₁+E₄+E₂,

I₁₁(R₂+R₁)+I₂₂(R₃+R₂+R₅+R₁)-I₃₃(R₁+R₃)=E₅+E₂+E₁-E₃,

-I₁₁R₁-I₂₂(R₁+R₃)+I₃₃(R₃+R₆+R₁)=E₃+E₆-E₁;

Подставив числа, получим:

26I₁₁+20I₂₂-13I₃₃=24,

20I₁₁+32I₂₂-22I₃₃=16,

-13I₁₁-22I₂₂+34I₃₃=13;

I₁₁=0,969 (А); I₂₂=0,742 (А); I₃₃=1,233 (А);

I₁=I₁₁+I₂₂-I₃₃; I₂=I₁₁+I₂₂; I₃=I₃₃-I₂₂;

I₄=I₁₁; I₅=I₂₂; I₆=I₃₃;

I1, А	I2, А	I3, А	I4, А	I5, А	I6, А
0,478	1,711	0,491	0,969	0,742	1,233

Расчёт токов по методу узловых потенциалов

Потенциал узла № 4 примем равным нулю

j₄=0;

j₁G₁₁+j₂G₁₂+j₃G₁₃=I₁₁,

j₁G₂₁+j₂G₂₂+j₃G₂₃=I₂₂,

j₁G₃₁+j₂G₃₂+j₃G₃₃=I₃₃;

Где j_i – потенциал i-го узла;

                             

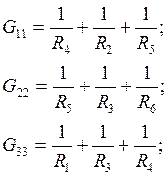
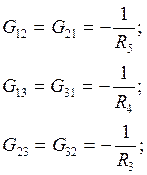
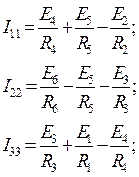
0,643j₁-0,333j₂-0,167j₃=-0,952,

-0,333j₁+0,528j₂-0,111j₃=1,083,

-0,167j₁-0,111j₂+0,353j₃=-1,333;

j1,В	j,В	j3,В
-4,024	-1,796	-6,212

                        

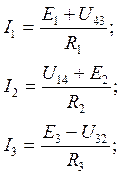
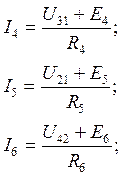
U_ik=j_i-j_k

I1, А	I2, А	I3, А	I4, А	I5, А	I6, А
0,478	1,711	0,491	0,969	0,742	1,233

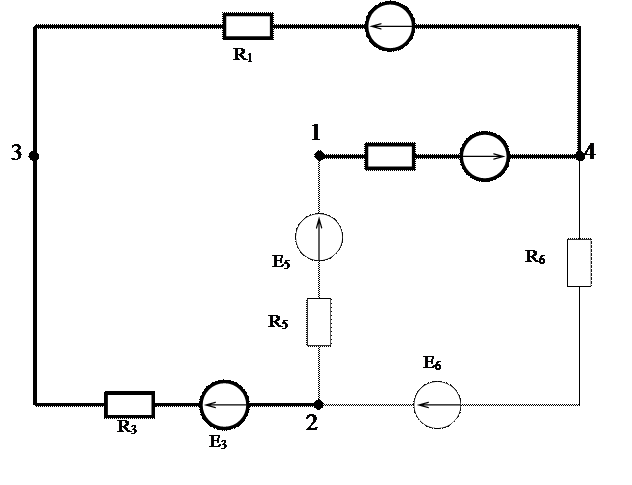
Расчёт тока в ветви 3-1 методом эквивалентного генератора

Схема эквивалентного генератора

 

E1

                                                                            

	R2
			E2

 

ЭДС E_э будет равна напряжению между точками 1 и 3, для расчёта которого применим метод узловых потенциалов.

Потенциал точки 4 примем равным нулю.

j₁G₁₁+j₂G₁₂+j₃G₁₃=I₁₁,

j₁G₂₁+j₂G₂₂+j₃G₂₃=I₂₂,

j₁G₃₁+j₂G₃₂+j₃G₃₃=I₃₃;

            

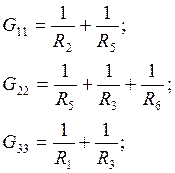
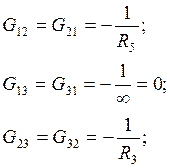
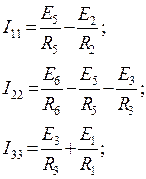
0,476j₁-0,333j₂+0j₃=-2,286,

-0,333j₁+0,528j₂-0,111j₃=1,083,

0j₁-0,111j₂+0,188j₃=0;

j1,В	j,В	j3,В
-6,381	-2,258	-1,334

E_э=j₃-j₁=5,046В

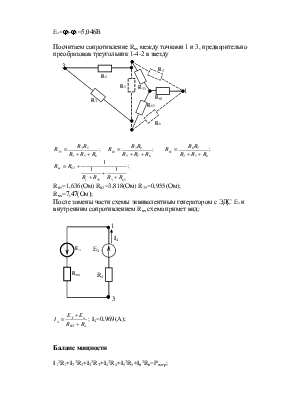
Посчитаем сопротивление R_вх между точками 1 и 3, предварительно преобразовав треугольник 1-4-2 в звезду

                                                                                

 

         

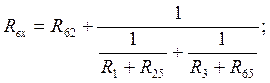
R₆₅=1,636(Ом) R₆₂=3,818(Ом) R₂₅=0,955(Ом);

R_вх=7,47(Ом);

После замены части схемы эквивалентным генератором с ЭДС E_э и внутренним сопротивлением R_вх схема примет вид:

 

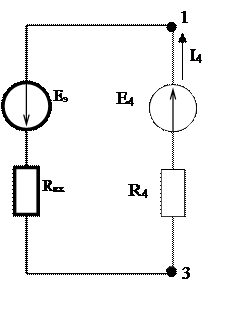 I₄=0,969(A);

Баланс мощности

I₁²R₁+I₂²R₂+I₃²R₃+I₄²R₄+I₅²R₅+I₆²R₆=P_потр;

E₁I₁+E₂I₂+E₃I₃+E₄I₄+E₅I₅+E₆I₆=P_ист;

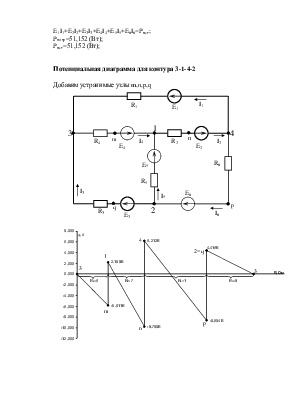
P_потр=51,152 (Вт);

P_ист=51,152 (Вт);

Потенциальная диаграмма для контура 3-1-4-2

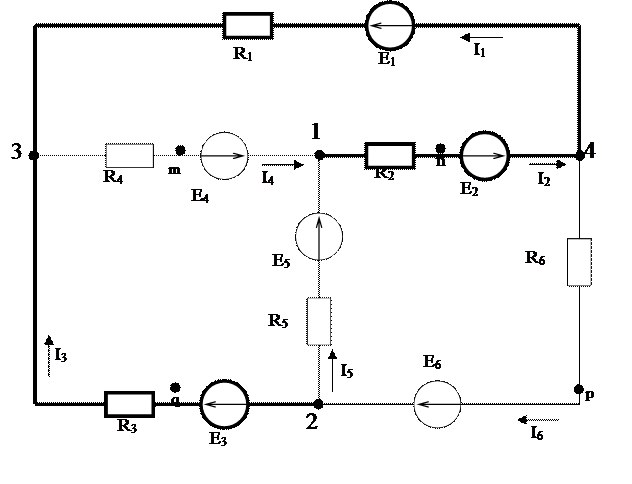
Добавим устранимые узлы m,n,p,q

 

3

2=q

p

4

n

1

m

3