φгн - объемное газосодержание в опускной трубе;
Wж- приведенная скорость жидкости (здесь и далее приведенные скорости фаз определяются как отношение расхода соответствующей фазы к площади сечения трубы), м/с.
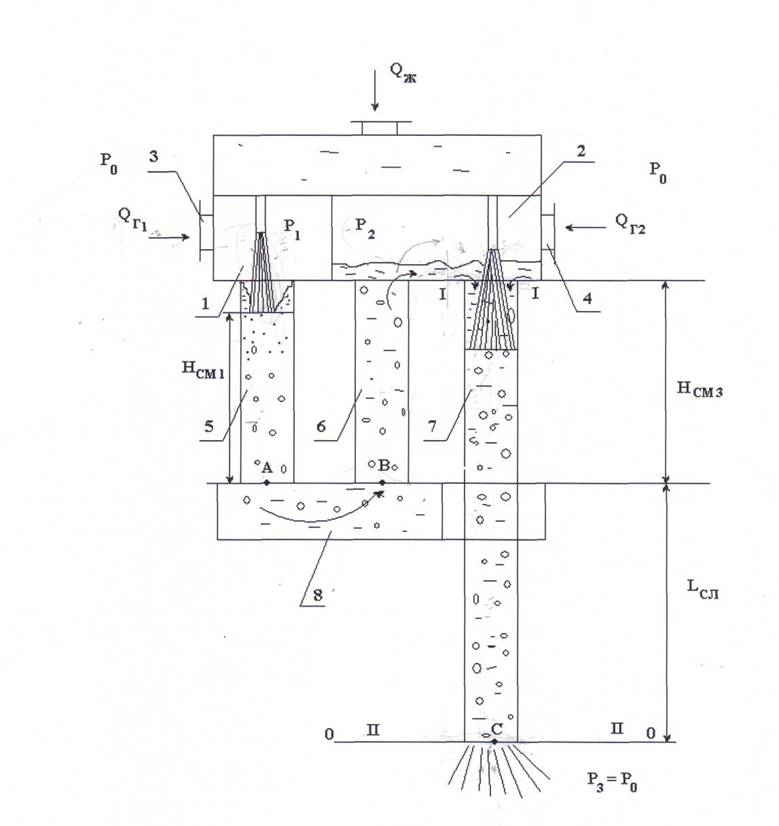
Рис. 7 Расчетная схема к выводу уравнения циркуляционного контура.
Потери энергии, связанные с расширением газожидкостного потока, ΔРР, оценить достаточно сложно, т.к. гидродинамика течений в газожидкостном конусе не изучалась [34]. Поэтому воспользуемся общим подходом к оценке местных сопротивлений в газожидкостных потоках и представим уравнение для расчета ΔРР в виде
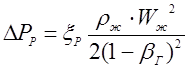 (23)
(23)
Потери энергии ΔРАР.Н также не представляется возможным оценить аналитически в связи с отсутствием надежных уравнений, описывающих сопротивление движению жидкости, которое оказывают архимедовы силы выталкивания, возникающие в вертикальном газожидкостном потоке.
Потери энергии, связанные с преодолением сил трения в подъемной трубе ΔРВ складываются из:
![]() (24)
(24)
где ΔРДЛ в - потери энергии по длине, связанные с трением жидкости о стенки трубы.
ΔРМ - местные потери, связанные с выходом газожидкостного потока из подъемной трубы.
ΔРАР.В - часть энергии, передаваемая архимедовыми силами всплывающих пузырьков, жидкости в восходящем потоке.
ΔРдл.в ~ определяются по уравнению (22).
Местные потери ΔРМ также могут быть определены по уравнению
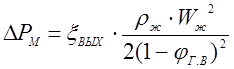 (25)
(25)
где ξвых - коэффициент сопротивления на выходе газожидкостного потока из трубы в резервуар бесконечно большого объема.
ΔРАР.Н и ΔРАР.В, входящие в уравнения (21) и (24) с некоторым допущением можно принять равными по значению и исключить их из баланса как взаимноуравновешивающие друг друга. Подставим найденные значения входящих, в уравнения (21) и (24) параметров, в уравнение баланса (19).
P 1 + ρ ж*V012 /2 (1 – β Г1) + ρ ж*g*H СМ1 (1 – φ Г.Н1) – λ Н*H СМ1*ρ ж*Wж12/d тр(1 – φ Г.Н) 1,75 - ξ Р* ρ ж* Wж2/2(1 – β Г ) 2 = P2 + ρ ж* g *H СМ2 (1 – φ Г.В) + λ В * H СМ2 * ρж * Wж2 2/d тр*2(1 – φ Г.В) 1,75 + ξВЫХ * ρж*Wж2 / 2(1 – φ Г.В)2 (26)
Перегруппируем слагаемые в уравнении (2.18), объединив потенциальную энергию в левой части уравнения, а гидравлические потери в правой части.
(P1 – P2)+ ρ ж*V012 /2 (1 – β Г1) + ρ ж*g*H СМ1 (1 – φ Г.Н1) – ρ ж* g *H СМ2 (1 – φ Г.В) = λ В * H СМ2 * ρж * Wж2 2/d тр*2(1 – φ Г.В) 1,75 + λ Н*H см1*ρ ж*Wж12/2d тр(1 – φ Г.Н) 1,75 + ξ Р* ρ ж* Wж12/2(1 – β Г ) 2 + ξВЫХ * ρж*Wж2 / 2(1 – φ Г.В)2 + ξ АВ* ρ ж* Wж2/2(1 – φ ср ) 2
(27)
и далее, преобразуя правую часть уравнения, приняв Wж2 = Wж1, получим
(P1 – P2)+ ρ ж*V012 /2 (1 – β Г1) + ρ ж*g*H СМ1 (1 – φ Г.Н1) – ρ ж* g *H СМ2 (1 – φ Г.В) = ρж*Wж2 / 2 [λ В * H СМ2 /d тр*(1 – φ Г.В) 1,75 + λ Н*H см1 /d тр(1 – φ Г.Н) 1,75 +ξ Р /(1 - β Г ) 2 + ξВЫХ / (1 – φ Г.В)2 + ξ АВ *2,75 / (1 – φ ср ) 2 ] (28)
В данном уравнении ξАВ - коэффициент местных сопротивлений при повороте потока на 180 градусов, определяется по рекомендациям работы [40].
Выражение, стоящее в правой части уравнения (28), есть коэффициент сопротивления контура, ξк, состоящего из опускной и подъемной труб. С учетом последнего замечания уравнение (28) примет вид
(P1 – P2)+ ρ ж*V12 /2 (1 – β Г1) + ρ ж*g*H СМ1 (1 – φ Г.Н1) – ρ ж* g *H СМ2 (1 – φ Г.В) = ξ K* ρ ж* Wж2/2 (29)
Уравнение (29)позволяет при заданном расходе QЖ1рассчитать значение давления Р2 , при котором будет происходить подача газовой фазы с расходом QГ2 в дополнительную камеру.
Возникает необходимость экспериментальным путём определить коэффициент сопротивления циркуляционного контура. Кроме того требуется исследовать начало устойчивого режима КСИА при его работе с дополнительным соплом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.