Типовые динамические звенья. Пропорциональное (безинерционное) звено. Интегральное звено (астатическое), страница 2

ВХ   w   h                                         h

k=w_c

 

                                                                          t

;

Два способа построения:

1)  На частоте w=1 L(w)=20lgk – I точка.

На частоте среза L(w_c)=0 à w_c=k –II точка.

2)  Находим наклон ЛАХ, т.е. приращение характеристики на декаду:

L(w_i)-L(10w_i)=-20дБ, т.о. через точку w_c нужно провести прямую с наклоном -20дБ/дек. В общем случае . Наклон - 20дБ/дек – просести через точку w_c.

           L(w)

                       -1

      20lgk

20дБ

 

k=w_c        w

           0.1       1               10             100lgw

3.4  Колебательное звено.

Примеры колебательных звеньев: цепочка RLC, гидромеханическое устройство.

Д.у. .

к- коэффициент передачи звена.

g – постоянная времени.

 - коэффициент затухания.

ПФ

IF 0<<1 – звено колебательное.

=0 – консервативное.

>=1 – апериодическое II порядка.

Пример: ЭДПТ.

 

                          e

I

                                                        w, M

U

r, L, Jд – физические параметры. Моментная постоянная М=cI; e=cw/

Две постоянные времени Ta=L/r – электромагнитная, Тм= - электромеханическая.

ПФ ЭД.

, сравниваем с (*), к=1/с,

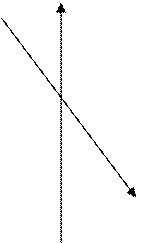
АФЧХ:

;

jV

 

w=

                                                            k

w=0        U

                 

   

             k/2                            W                        w

 

w=1, т.е. w=1/T

ФЧХ:

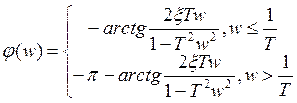
АЧХ:

.

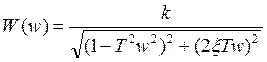1.

2.  - частота сопряжения,

3. W(w) достаточно максимальна на резонансной частоте  т.е. меньше опорной. При этом .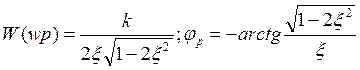

4.

При  резонансная частота w_p=0, а W(w)=k.

При <0.707 резонансная частота w_p<w₀ , а W(w)>k.

Чем меньше , тем выше резонансный пик.

При =0, колебательное звено становится консервативным, при этом W(w₀)=.

, .

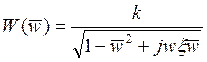При  0.707<<1 – амплитуда W уменьшается с увеличением w, т.е. W(w)k.

=T₁/(2T₂) – коэффициент затухания. Постоянная Т₂ – раскачивает колебания, Т₁ – демпфирует их.

ФЧХ

 

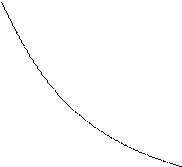
W()                                   =0

                       =0.4

=0.7

                         

                         =1

 

=1

 

                                                                                  

 

                                         =0 (консервативное звено)

-450

                                                                  =1

-900

ЛАЧХ:

- грубое приближение.

 

                       =0                     ЛАХ     

L(w)

                         

20lgk                             

40дБ/дек

                                                                                     w

w₀=1/T                

1) <<1 L(w)=20lgk – НЧ асимптота.

2) >>1  - в частности, асимптота наклонена 40дБ/дек.

Из условия L(w)=0 (в/ч асимптота) à  

Точная ЛАХ может значительно отличается от аситпточеской при малых . Величина отклонения на опорной части. .

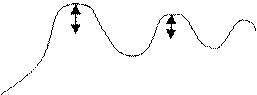
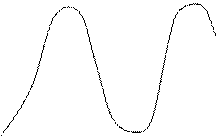
Переходная характеристика колебаний звена.

h(t)

                   А₁               А₂ 

 

к

 

0                                                                 t

 

Тк

.

Передаточный коэффициент к – определяют по установившемуся значению  переходной функции.

3.4.1 Консервативное звено (=0).

                                                                                        jV

ПФ: .

Частотная ПФ: .              1/Tßwà     w=0  wà1/T

ФЧХ:                                                 0     k                      U

                                    ЛЧХ                                 ПФ

     L(w)                                           h(t)                    =0

 

20lgk                                                       k

lgw                                                             t

 

w₁=1/T

-90⁰

Затуханий нет.

3.4.2 Апериодическое звено ().

ФП при можно преобразовать к виду 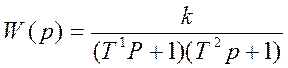, где Т1,2=, т.е. это последовательно соединение двух звеньев.

АФЧХ: ;

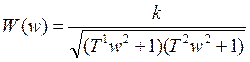АЧХ: ;

ФЧХ: .

 

jV                                                       W

 

k

U

        _w=                                                                                                                                                                                     w

                                            w

                           W                                                                                    w

                                                          -90⁰

                                                                          -180⁰

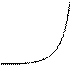
ЛАЧХ: .

          L(w)

                                -20дБ/дек                             =1                         7.5%

20lgk

-40дБ/дек                                    

 

0    1             1/T1        1/T₂

ПХ: .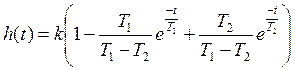

Примером такого звена является ДПТ при учете инерционности цепи якоря, электромагнитный усилитель, двойная цепочка R,L.