1.1 В ы б о р э л е к т р о д в и г а т е л я
При постоянной нагрузке необходимая мощность
электродвигателя (Рэд)
определяется по формуле: 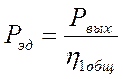
![]() - мощность выхода привода
определяется по формуле:
- мощность выхода привода
определяется по формуле:
![]()
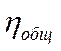 - общий КПД привода:
- общий КПД привода:
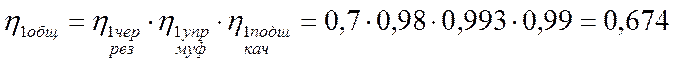
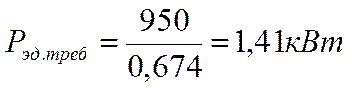
Определяем частоту вращения выходного вала:
Из уравнения ![]() следует:
следует:
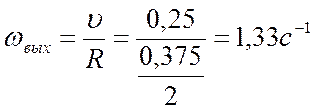 .
.
В свою очередь
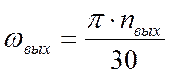 . (1)
. (1)
Из уравнения (1)
находим 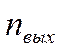 :
:
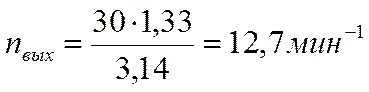 ;.
;.
Требуемая частота вращения электродвигателя равна:
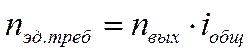 ;
;
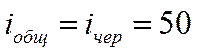 ;
;
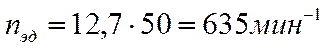 .
.
Выбираем электродвигатель типа:
![]() ,
, ![]() .
По таблице 2.2.[1, с.26] выбираем двигатель 4А100L8Y3, у которого S=7,0%,
.
По таблице 2.2.[1, с.26] выбираем двигатель 4А100L8Y3, у которого S=7,0%, 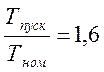 ,
, ![]() ,
P=1,5кВт.
,
P=1,5кВт.
Проверка двигателя на пуск:
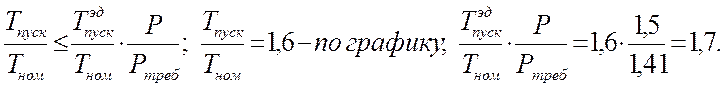
Проверяем условие пуска двигателя:
![]() -проверка сходится.
-проверка сходится.
То есть окончательно принимаем электродвигатель 4А100L8Y3.
![]()
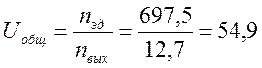 ;
;
![]()
1.3. О п р е д е л е н и е к р у т я щ е г о м о м е н т а (Т) н а в а л а х
Определяем ![]() со стороны выходного вала:
со стороны выходного вала:
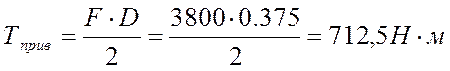 ;
;
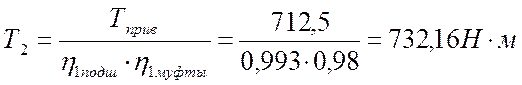 ;
;
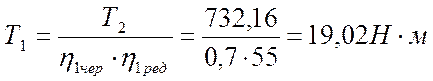 ;
;
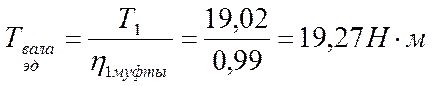
Определим частоты вращения валов:
![]() ;
;
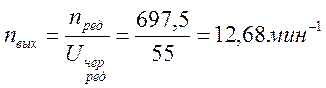 .
.
2. Расчет червячного редуктора.
Исходные
данные: ![]() ,
, ![]() ,
,
![]() , U=55,
, U=55, ![]() ,
, ![]() ,
,
![]() .
.
Ожидаемая скорость скольжения по формуле 7.6. [1]:
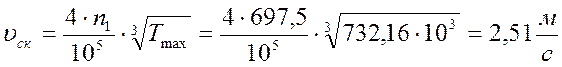 .
.
Коэффициент эквивалентности по контактной выносливости по формуле 4.5. [1, с.80]:
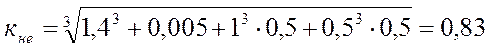 .
.
Продолжительность
включения 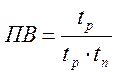 , где
, где ![]() и
и
![]() - время работы и время пауз в
пределах среднего цикла, а т.к. в нашем случае время пауз не задано, то будем
считать, что оно равно нулю. Т.к. ПВ=1, то произведение
- время работы и время пауз в
пределах среднего цикла, а т.к. в нашем случае время пауз не задано, то будем
считать, что оно равно нулю. Т.к. ПВ=1, то произведение ![]() .
.
По таблице 7.1. [1, с.212] выбираем материал группы Iб, а именно Бр05Ц5С5. Для бронз групп I расчет ведут по эквивалентному моменту, определив коэффициент долговечности согласно §7.3 [1].
Машинное время работы по формуле 4.12. [1, с.82]:
![]() .
.
Наработка:
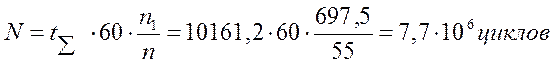 .
.
Коэффициент долговечности по формуле 7.2. [1, с.209]:
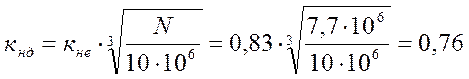 .
.
Коэффициент эквивалентности по изгибу по формуле 4.13. [1]:
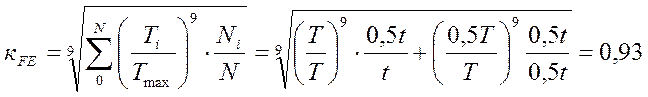 .
.
Коэффициент долговечности по формуле 7.4. [1, с.210]:
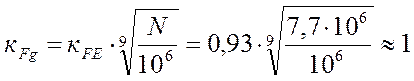 .
.
Согласно §7.4.
[1] принимаем червяк из стали 18ХГТ с цементацией и закалкой до твердости HRC 56 – 63. Допускаемое напряжение по табл.7.3. [1]: ![]() . По рис. 7.1. [1] для
. По рис. 7.1. [1] для 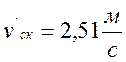 ,
, ![]() .
.
Предел
прочности для бронзы Бр05Ц5С5 по табл. 7.1. [1] при литье в кокиль ![]() :
:
![]()
Предварительный
коэффициент нагрузки по формуле 7.7.[1, с.213] ![]() .
Коэффициент концентрации по формуле 7.8. [1, с.214]
.
Коэффициент концентрации по формуле 7.8. [1, с.214] ![]() .
Заходность червяка при U=55, z1=1
(см.[1, с.216]). Начальный коэффициент концентрации по рис.7.2.[1] при z1=1 и U=55
.
Заходность червяка при U=55, z1=1
(см.[1, с.216]). Начальный коэффициент концентрации по рис.7.2.[1] при z1=1 и U=55 ![]() , тогда
, тогда ![]() .
.
Согласно §7.6.
kv`=1, ![]() .
.
Предварительное значение межосевого расстояния по формуле 7.11. [1, с.216]:
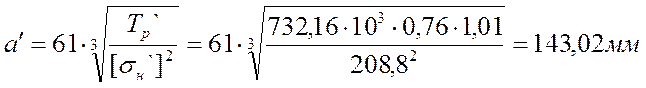 .
.
Принимаем стандартное ближайшее межосевое расстояние а=140мм[1, с.51].
Число зубьев колеса по формуле 7.12.[1, с.216] z2`=z1U=55
Модуль по формуле 7.13.[1, с.216]:
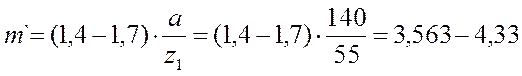 .
.
Принимаем стандартный модуль m=4 [1,с.53].
Коэффициент диаметра червяка по формуле 7.14.[1,с.216]:
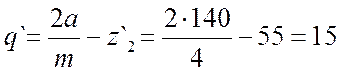
Окончательно принимаем z2=55 [1,c.217], q=14 [1,c.56].
Коэффициент смещения по формуле 7.15. [1, с.216]:

Угол подъема витка на начальном диаметре, при x=0,5 по формуле 7.17.[1, с.216]:
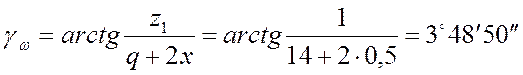 .
.
Угол подъема линии витка на делительном диаметре по формуле 7.30. [1, с.223]:
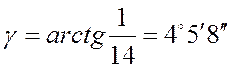 .
.
Длина червяка по формуле 7.18. и табл. 7.5. [1]:
![]() .
.
Принимаем b1=73мм.
Проверяем
фактическое контактное напряжение по формуле 7.21.[1, с.216] 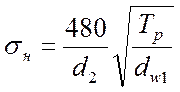 .
.
Делительный диаметр колеса по формуле 7.32. [1, с.223]:
d2=mz2=4*55=220мм.
Начальный диаметр червяка при х=0,5:
![]() .
.
Фактическая скорость скольжения по формуле7.22. [1, с.218]:
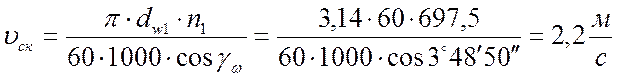 .
.
Коэффициент концентрации по формуле 7.9. и табл.4.1. и 7.4.[1]:
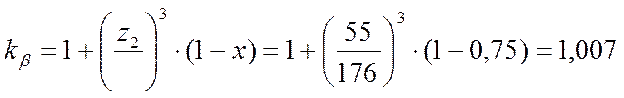 .
.
Скорость колеса по формуле 7.10. [1, с.215]:
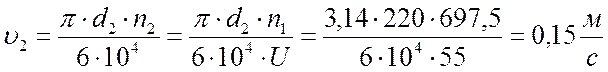 .
.
Коэффициент динамичности по табл. 4.11. [1, с.96] для 9 степени точности табл. 4.10. [1, с.96] kv=1,01. По формуле 7.7. [1, с.213]:
![]() .
.
Расчетный момент:
![]() .
.
Напряжение:
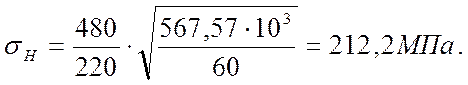
Уточняем
допускаемые напряжение по фактической скорости скольжения 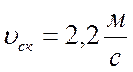 . Тогда:
. Тогда:
![]() .
.
При этих значениях допускаемого и фактического напряжений появляется запас по напряжению в 2%, что не превышает 10% и поэтому удовлетворяет условиям поставленной задачи.
Проверяем статическую контактную прочность. Предельное контактное напряжение по табл.7.3. [1]:
![]() .
.
Максимальное контактное напряжение по формуле 4.43. [1, с.99]:
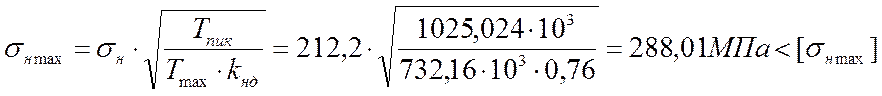 .
.
Проверяем напряжение изгиба. Допускаемое напряжение изгиба по табл. 7.3. [1]:
![]() .
.
Напряжение изгиба в зубьях колеса по формуле 7.24. [1,с.219]:
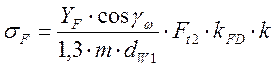 .
.
Эквивалентное число зубьев колеса по формуле 7.25. [1]:
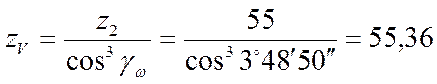 .
.
Коэффициент формы зуба YF=1,4[1, с.219]. Значение получено с использованием линейной интерполяции.
Окружная сила на колесе по формуле 7.23. [1, с.219]:
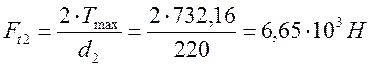 ;
;
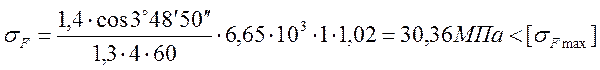 .
.
Окончательно принимаем основные параметра редуктора:
межосевое расстояние а=140мм;
передаточное отношение U=55;
число витков червяка z1=1;
число зубьев колеса z2=55;
модуль зацепления m=4 мм;
коэффициент диаметра червяка q=14;
коэффициент смещения х=0,5;
угол подъема
линии витка на делительном диаметре ![]() ;
;
угол подъема
линии витка на начальном цилиндре ![]() ;
;
длина неразрезанной части червяка b1 =73мм;
ширина витка червячного колеса b2=50мм.
2.1.1.Геометрический расчет червячной передачи.
Определяем делительный диаметр червяка по формуле 7.26. [1, с.223]:
![]()
Диаметр вершин витков находим по формуле 7.28 [1, с.223]:
![]()
Диаметры впадин витков по формуле 7.29. [1, с.223]:
![]()
Угол подъема линии витка на делительном диаметре по формуле 7.30. [1, с.223]:
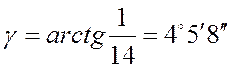 .
.
Угол подъема витка на начальном диаметре, при x=0,5 по формуле 7.17.[1, с.216]:
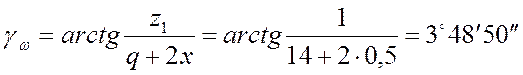 .
.
Делительный диаметр колеса по формуле 7.32. [1, с.223]:
d2=mz2=4*55=220мм.
Диаметр вершин зубьев по формуле 7.33. [1, с.223]:
![]() .
.
Наибольший диаметр колеса по формуле 7.34. [1, с.223]:
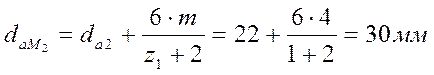 .
.
Диаметр впадин по формуле 7.35. [1, с.223]:
![]() .
.
Радиус закругления колеса по формуле 7.36. [1]:
![]() .
.
2.1.2. Силы в зацеплении червячной пары.
Окружная сила по формуле 7.23. [1, c.223]:
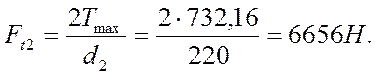
Осевая сила на червяке:
![]()
Окружная сила на червяке по формуле 7.38. [1, с.225]:
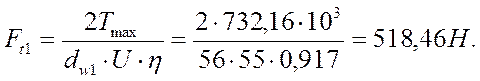
Осевая сила на червячном колесе:
![]()
Радиальная сила по формуле 7.39. [1, с.225]:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.