




Лабораторная работа
№6
“ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ КОРОТКОГО СОЛЕНОИДА И СИСТЕМЫ ДВУХ СОЛЕНОИДОВ”
ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ КОРОТКОГО СОЛЕНОИДА И СИСТЕМЫ ДВУХ СОЛЕНОИДОВ
Цель работы:
Введение
Индукция магнитного поля ![]() ,
создаваемого элементом проводника
,
создаваемого элементом проводника ![]() , по которому
протекает ток
, по которому
протекает ток ![]() в точке пространства,
которая находится на расстоянии
в точке пространства,
которая находится на расстоянии ![]() от элемента тока
от элемента тока
![]() , описывается законом
Био-Савара-Лапласа:
, описывается законом
Био-Савара-Лапласа:
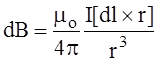 (1)
(1)
Используя уравнение (1) найдем величину магнитного поля на оси витка, по которому проходит постоянный электрический ток,
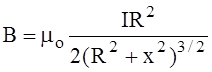 (2)
(2)
где
![]() - радиус кругового витка с током,
- радиус кругового витка с током, ![]() - расстояние вдоль оси от центра
круга до точки М на оси кругового тока, в которой измеряется магнитное поле.
Индукция кругового тока в его центре (
- расстояние вдоль оси от центра
круга до точки М на оси кругового тока, в которой измеряется магнитное поле.
Индукция кругового тока в его центре (![]() )
равна:
)
равна:
![]() (3)
(3)
На рис.1 видно, что
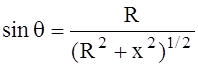 (4)
(4)
|
|
Тогда соотношение (2) может быть записано в виде
![]() (5)
(5)
Совокупность близко расположенных круговых витков с током, центры которых лежат на общей оси, составляют соленоид. Магнитное поле на оси соленоида можно вычислить, как суму полей, создаваемых каждым витком с током (принцип суперпозиции).
Соленоид называется коротким, если его длина ![]() значительно меньше радиуса обмотки
соленоида
значительно меньше радиуса обмотки
соленоида ![]() , и наоборот длинным, если
, и наоборот длинным, если ![]() .
.
|
|
Определим индукцию в точке ![]() (рис.2)
для соленоида длиной
(рис.2)
для соленоида длиной ![]() , радиусом
, радиусом ![]() и числом витков
и числом витков ![]() (т.е. плотностью намотки, или
числом витков на единицу длины
(т.е. плотностью намотки, или
числом витков на единицу длины ![]() ). Вклад участка
соленоида длиной
). Вклад участка
соленоида длиной ![]() в результирующее
магнитное поле равен:
в результирующее
магнитное поле равен:
![]() (6)
(6)
Запишем
переменную ![]() через угол
через угол ![]() .
На рис. 2 видно, что
.
На рис. 2 видно, что ![]() , откуда
, откуда ![]() . Тогда
. Тогда ![]() интегрируя
это выражение по углу
интегрируя
это выражение по углу ![]() , получим:
, получим:
![]() (7)
(7)
|
|
где
![]() и
и ![]() -
углы, под какими видно радиусы соленоида из точки на его оси, в которой
вычисляется магнитное поле (рис. 2). Если точка на оси лежит внутри соленоида,
то удобно ввести угол
-
углы, под какими видно радиусы соленоида из точки на его оси, в которой
вычисляется магнитное поле (рис. 2). Если точка на оси лежит внутри соленоида,
то удобно ввести угол ![]() (рис. 3). Тогда формула
(7) с учетом формулы (3), принимает вид:
(рис. 3). Тогда формула
(7) с учетом формулы (3), принимает вид:
![]() (8)
(8)
Магнитное поле в центре короткого соленоида равно
![]() (9)
(9)
|
|
|
Принцип суперпозиции магнитных полей можно проверить
экспериментально, используя два коротких соленоида (катушки Гельмгольца).
Результирующее поле в точке М (рис.4) при этом определяется алгебраической
суммой полей, которые создаются каждой катушкою отдельно, а распределение ![]() вдоль оси соленоидов будет
определяться суммой кривых
вдоль оси соленоидов будет
определяться суммой кривых ![]() и
и ![]() , создаваемых каждой катушкой
отдельно (рис. 5).
, создаваемых каждой катушкой
отдельно (рис. 5).
На рис.5 проиллюстрирована суперпозиция полей, создаваемых катушками Гельмгольца при протекании токов одинакового направления.
Описание экспериментальной установки
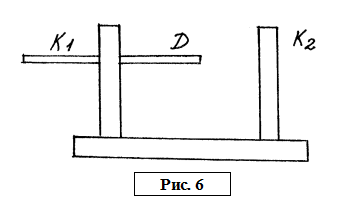 Описание установки показано на рис. 6. Катушка
Описание установки показано на рис. 6. Катушка ![]() неподвижна, а катушка
неподвижна, а катушка ![]() может перемещаться по направляющим.
Расстояние между центрами катушек определяется по шкале, которая располагается
на панели. Измерительный датчик D закреплен на стержне, который может
перемещаться вдоль оси соленоида. Датчик позволяет измерять индукцию магнитного
поля на оси системы. Переменный ток, который протекает по соленоиду, создает в
пространстве переменное магнитное поле, которое возбуждает в катушке D
электродвижущую силу индукции (ЭДС):
может перемещаться по направляющим.
Расстояние между центрами катушек определяется по шкале, которая располагается
на панели. Измерительный датчик D закреплен на стержне, который может
перемещаться вдоль оси соленоида. Датчик позволяет измерять индукцию магнитного
поля на оси системы. Переменный ток, который протекает по соленоиду, создает в
пространстве переменное магнитное поле, которое возбуждает в катушке D
электродвижущую силу индукции (ЭДС):
![]() (10)
(10)
где
![]() - поток вектора индукции магнитного
поля через катушку,
- поток вектора индукции магнитного
поля через катушку, ![]() - площадь сечения катушки
датчика,
- площадь сечения катушки
датчика, ![]() - число витков катушки датчика.
Учитывая, что
- число витков катушки датчика.
Учитывая, что
![]() (11)
(11)
получим
![]() , (12)
, (12)
где
линейная частота переменного тока ![]() .
.
Измерения ![]() можно проводить
или вольтметром, или при помощи осциллографа. В связи с тем, что входное
сопротивление вольтметра очень велико, можно записать, что
можно проводить
или вольтметром, или при помощи осциллографа. В связи с тем, что входное
сопротивление вольтметра очень велико, можно записать, что
![]() . (13)
. (13)
Тогда
из (12) с учетом соотношения (13), можно получить амплитудное значение индукции
магнитного поля ![]()
![]() , (14)
, (14)
где
![]() .
.
При использовании осциллографа
![]() . (15)
. (15)
Радиусы коротких соленоидов ![]() ,
длины намотки
,
длины намотки ![]() , число витков обмоток
соленоидов
, число витков обмоток
соленоидов ![]() .
.
Выполнение работы
1. Показать, что соленоид, который используется, можно считать коротким. Для этого, используя геометрические размеры соленоида, сравнить формулы (3) и (9). При этом принять число витков одинаковыми.
2.
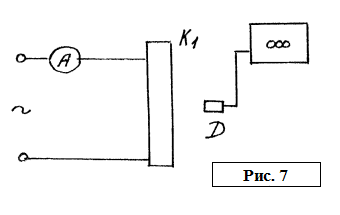 Собрать схему показную на
рис.7, используя неподвижную катушку
Собрать схему показную на
рис.7, используя неподвижную катушку ![]() . Установить ток
через соленоид
. Установить ток
через соленоид ![]() . С помощью измерительного
датчика
. С помощью измерительного
датчика ![]() найти индукцию
найти индукцию ![]() в центре соленоида. Перемещая зонд
вдоль оси соленоида, измерять поле первой катушки
в центре соленоида. Перемещая зонд
вдоль оси соленоида, измерять поле первой катушки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.