Линейное программирование (Составление суточного рациона для скота), страница 3

А) Сначала строят границу полуплоскости в виде прямой

Б) С помощью контрольной точки выбирают нужную плоскость

Таким образом строят все ограничения.

1)  Выбирают общую для всех ограниченную область , которая и будет ОДР  задачи.

В данной задаче 4-x угольник ABCD. Каждая точка области является допустимым решением задачи.

Нужно найти точку, в которой функция принимает значение min, для этого нужно построить два произвольных значения целевой функции F , для того, чтобы определить направление её роста. Значения задаются произвольно.

F1=6=3x1+2x2 (2;0)(0;3)

F2=0 ║ F1 через (•) (0;0)

Нашли направление роста F. Двигая в направлении прямой F параллельно самой себе, доходим до крайней точки на ОДР.

В точке C функция достигает своего max : fmax в (•) (x1*;x2*).

Найдём координаты этой точки. Точка C образована пересечением ограничений 1 и 3 .

Решим систему :

 

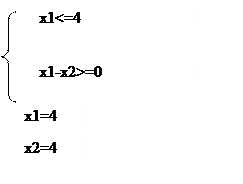Подставим  координаты в выражение целевой функции :

Fmax = 3*4+2*4=20

Ответ : Fmax = 20 , x1=4 , x2=4

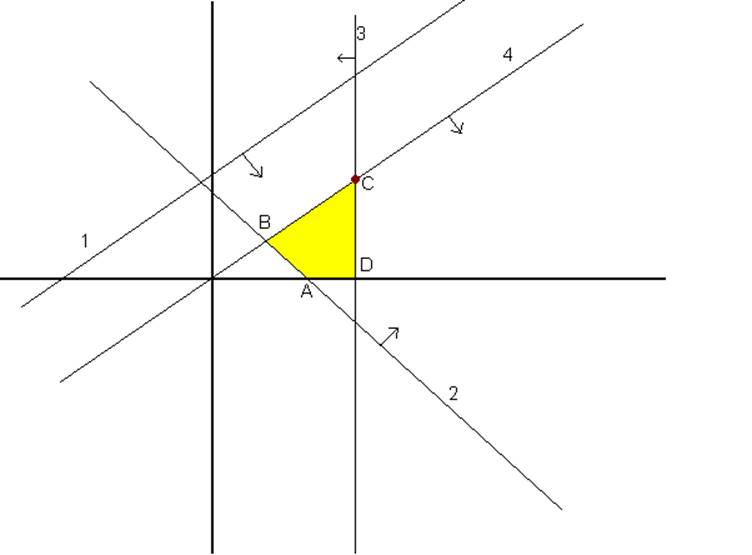
Рисунок 2.1

3. Решение транспортной задачи

3.1 Определение начального плана методом С-З угла

1) Сравниваем величины а1 и b1, возможны три варианта:

а) а1<b1, тогда => х11=а1, b1 =  b1-а1

При этом первая строка выходит из рассмотрения.

б) b1 < a1 => x11 = b1 , a1 = a1-b1

При этом первый столбец выходит из рассмотрения.

c) a1 = b1 => x11 = a1 = b1

При этом и первая строка  и первый столбец выходят из рассмотрения и в дальнейшем будем иметь вырожденное решение.

2) Выбирают следующую Северо-Западную клетку и аналогично сравнивают

аi с bj, выбирая из них меньшее и т.д..       

3) Последняя клетка заполняется автоматически.

4) Проверяем количество заполненных клеток в таблице, их должно быть m+n-1. Если количество заполненных клеток оказалось меньше,  чем m+n-1, то решение вырождено и необходимо в этом случае дополнить недостающее количество,  чтобы получилось m+n-1. Для этого в клетку ставят 0, считая эту клетку заполненной.

Внимание: При постановке  0 не должно получаться замкнутых прямоугольников.

3.1 Метод потенциалов для оптимизации решения транспортной задачи

	90		110		60		200		100		100
		6		7		7		5		9		0
200	90		-		60		50		-		-
		m		4		m		7		8		0
290	-		110		-		150		30		-
		7		6		6		8		11		0
250	-		-		-		-		70		180
	V1=	6	V2=	2	V3=	7	V4=	5	V5=	6	V6=	-5
	F1=	3710