Линейное программирование (Составление суточного рациона для скота), страница 2

0	S1	28	4	0	5	1	-0,5	0	0
0	S2	44	-2	0	-3	0	1	1	-1
0	x2	11,75	0,25	1	0,25	0	0,125	0	0
		0	0	0	0	0	-1	0	-1

Рисунок 1.1. Решение первого этапа

Решение второго этапа представлено на рисунке 1.2.

		0	11	13	10	0	0	Отношение
	Базис	x0	x1	x2	x3	S1	S2
0	S1	28	4	0	4	1	0	7	MIN
0	S2	44	-2	0	-3	0	0	x
13	x2	11,75	0,25	1	0,25	0	-1	47
	F	152,75	-7,75	0	-6,75	0	-13

11	x1	7	1	0	1	0,25	0
0	S2	58	0	0	-1	0,5	0
13	x2	10	0	1	0	-0,063	-1
	F	207	0	0	1	1,9375	-13

Рисунок 1.2. Решение второго этапа

Ответ выписывается из последней итерации: x1 ровняется числу из столбца x0 стоящему напротив x1 и так далее. Запись ответа представлена на рисунке 1.3.

Ответ:
Fmax=	207
x1=	7
x2=	10
x3=	0

Рисунок 1.3.Ответ

1.3 Реализация задачи линейного программирования на ПК

Для реализации задачи на ПК была использована программа Microsoft Excel.

Далее представлены формулы, используемые при реализации задачи:

2. Графический метод решения задачи линейного программирования

2.1 Задача

2.2 Анализ задачи и ее решение

(x)=2x1-3x2→min

Линейный характер модели состоит в том , что и целевая функция и ограничения носят линейный характер.

В общем виде любая задача линейного программирования сводится к следующей модели :

Целевая функция – f =   c * x  →max(min)

Ограничения A*X<=B , где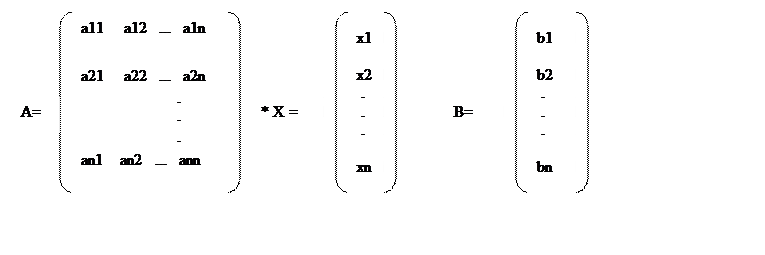  

Если существует хотя бы единственное решение , то ограничения называются совместными, иначе – не совместные.

В задаче может быть единственное решение, а может и бесчисленное количество. Множество решений задачи состоит в Области Допустимых

Решений (ОДР) , на которой мы ищем оптимальное решение, т.е. f→max или f→max.

Если число переменных в задаче  <= 2 , то возможно её графическое решение на плоскости, а именно в координатной сетке x1 0 x2.

При графическом решении задачи ЛП отмечают следующие этапы:

1)Строят координатную плоскость x1 0 x2

Выбирают подходящий масштаб и на плоскость наносят систему ограничений задачи следующим образом: