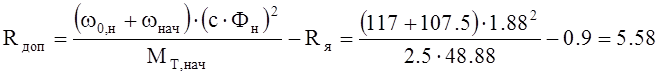Расчет искусственных механических характеристик двигателя с независимым возбуждением

 Ом.

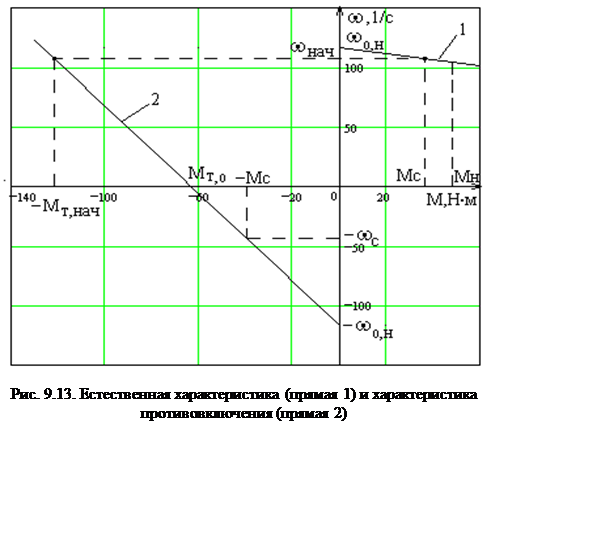
На рис. 9.13 построены естественная характеристика и характеристика режима противовключения. Отсюда (рис 9.13) видно, что механическая характеристика  2  пересекает ось абсцисс в точке, в которой момент двигателя имеет значение:

.

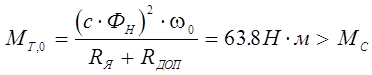Следовательно, двигатель может самопроизвольно среверсироваться, и разогнаться до скорости:

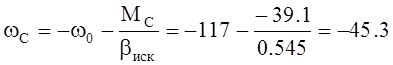 1/с,

где 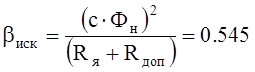  Н× м×с - модуль жесткости искусственной механической характеристики.

Пример 9

Двигатель (рассмотренный в примере 6) переключается с естественной механической характеристики при  в режим динамического торможения с независимым возбуждением. Найти величину тормозного сопротивления (R_Т), на которое подключается обмотка якоря для ограничения начального тормозного момента до значения М_Т,НАЧ =. Что произойдет с двигателем после его торможения до , если М_С - активный?

Решение

Величина тормозного сопротивления может быть вычислена как

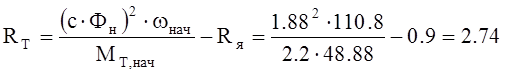 Ом, где  1/с - начальное значение скорости, с которой двигатель переключается в режим торможения.

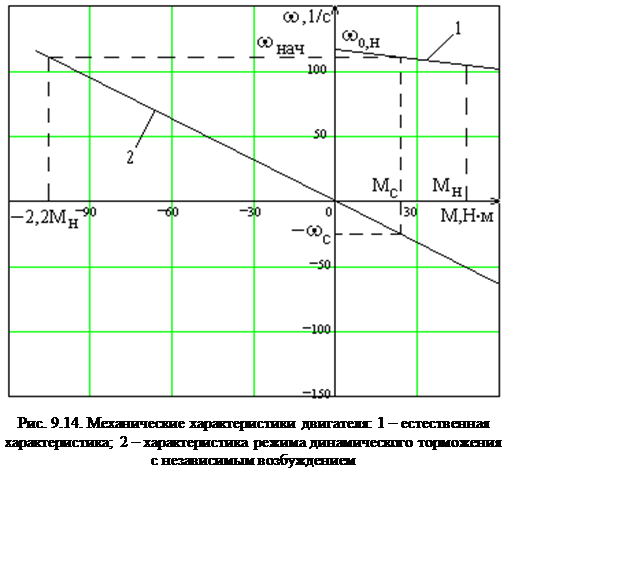
При наличии активного статического момента на валу двигателя, последний  после торможения разгонится в обратном направлении до скорости w_с (рис. 9.14):

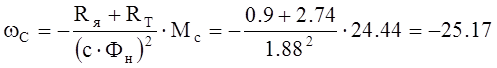 1/с.

Пример 10

Рассчитать искусственные механические характеристики двигателя с независимым возбуждением, соответствующие изменению: а) магнитного потока двигателя ; б) напряжения на якоре ; в) сопротивления якорной цепи .

Номинальные данные двигателя: Р_H = 32 кВт; U_H = 220 В; n_H =980об/мин;
I_Я,Н = 165 А; полное сопротивление якорной цепи при нагретой машине  

Решение

Коэффициент ЭДС двигателя при номинальном потоке:

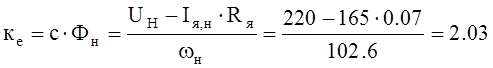 В с.

Здесь  1/с.

Скорость идеального холостого хода при номинальном потоке двигателя:

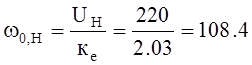 1/с.

Модуль жесткости естественной механической характеристики:

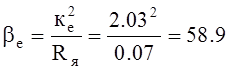 Н м с.

Уравнение естественной механической характеристики:

Номинальный электромагнитный момент двигателя:

Естественная механическая характеристика имеет вид (рис. 9.15, прямая 1).

Коэффициент ЭДС при ослабленном магнитном потоке:

 В с.

Скорость идеального холостого хода при ослабленном магнитном потоке:

 1/с.

Модуль жесткости механической характеристики при ослабленном поле:

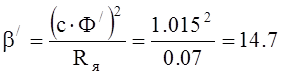 Н м с.

Уравнение механической характеристики при ослабленном поле :

Механическая характеристика при ослабленном поле имеет вид (рис. 9.15, прямая 2).

Скорость идеального холостого хода при пониженном напряжении питания :

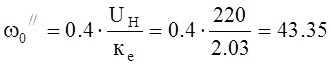 1/с.

Уравнение механической характеристики при

Соответствующая  характеристика представлена  на рис. 9.15 (прямая 3).

Номинальное сопротивление двигателя:

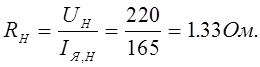
Заданное суммарное сопротивление якорной цепи для расчета реостатной характеристики:

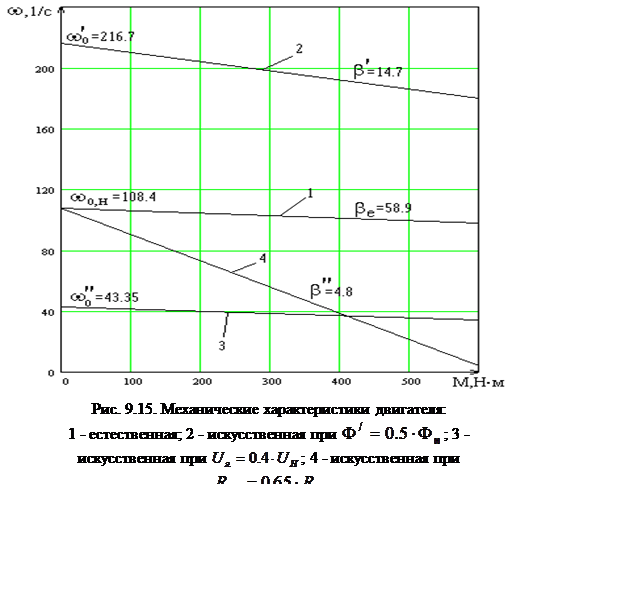
 Ом.

Модуль жесткости реостатной механической характеристики:

 Н м с.

Уравнение реостатной механической характеристики:

Для построения этой характеристики определим момент короткого замыкания:

Реостатная механическая характеристика, соответствующая , имеет вид (рис. 9.15, прямая 4).

Пример 11

Рассчитать механическую характеристику двигателя с независимым возбуждением в режиме динамического торможения с самовозбуждением, обеспечивающего при w_нач = w_н начальный тормозной момент М_т,нач = 2 М_н . Определить величину критической скорости, при которой пропадает тормозной эффект.

Данные двигателя: ; ; ; ;  ;  ;  ;    (сопротивления обмотки якоря и обмотки возбуждения в нагретом состоянии).

Решение

Известно, что при заданном сопротивлении цепи возбуждения машина может возбудиться лишь при некотором критическом значении скорости (w_кр). При этом вольтамперная характеристика цепи возбуждения должна пересекать характеристику холостого хода, т.е. должно выполняться условие: .

Схема переключения двигателя в режиме динамического торможения с самовозбуждением показана на рис. 9.16. При размыкании контакта К1, замыкается контакт К2 и якорь вместе с обмоткой возбуждения подключаются к сопротивлению R_т.

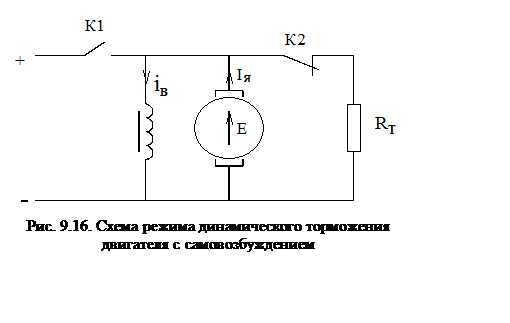Для расчета механических характеристик в режиме динамического торможения с самовозбуждением необходимо иметь в распоряжении кривую намагничивания и данные о сопротивлении обмотки возбуждения. Так как при неизменном токе возбуждения ЭДС пропорциональна скорости, то кривую намагничивания можно перестроить для ряда значений скорости. Точки пересечения вольтамперной характеристики  с кривыми намагничивания определяют токи возбуждения при соответствующей скорости.

На рис. 9.17 построены кривые намагничивания для ряда значений скорости и там же нанесена линия, характеризующая зависимость .

Коэффициент ЭДС при номинальном потоке двигателя:

.

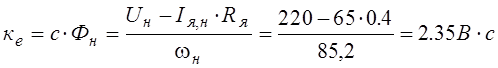Конструктивный коэффициент:

.

Номинальный электромагнитный момент:

.