Турбулентный пограничный слой с химическими реакциями

	Q

Г л а в а   6

      ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

       С ХИМИЧЕСКИМИ РЕАКЦИЯМИ

6.1.  Тепломассообмен на реагирующей

        поверхности

           роблема  пограничного  слоя  с  химическими  реакциями

           представляет самостоятельный интерес. Она охватывает широкий круг явлений, начиная с различных видов горения топлив и кончая взаимодействием высокоскоростных газовых потоков с химически активными поверхностями. Большое практическое значение имеют реакции углерода с газами, поскольку графит и другие углеродсодержащие материалы широко применяются в различных отраслях современной техники. Значительная часть потребности в энергии удовлетворяется путем прямого или косвенного использования реакций углерода с газами.

В пограничном слое могут происходить как гомогенные, так и гетерогенные химические реакции. Гетерогенные – когда твердая стенка сама принимает участие в реакциях. Скорость гетерогенных реакций обусловлена двумя факторами: 1) диффузией реагирующего газа из невозмущенного потока через пограничный слой к поверхности, 2) скоростью протекания самой химической реакции (реакционной способностью).

При низких температурах скорость протекания химической реакции ниже скорости диффузии, поэтому определяющим является кинетический режим. С увеличением температуры скорость реакции возрастает и преобладающей всего процесса является скорость диффузии, что характеризует диффузионный режим реагирования. На рис. 6.1 показана зависимость интенсивности выгорания графита в потоке воздуха от температуры стенки. Видно, что при температурах до 1400 К наблюдается сильная зависимость от температуры, что характерно для кинетического режима, при Т_cт > 1400 К имеет место диффузионный режим.

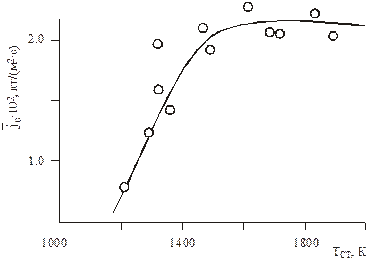
Рис.6.1. Зависимость интенсивности выгорания графита

от температуры в потоке воздуха. U₀ ~ 90 м/с, T₀ ~ 290 K

В реагирующем пограничном слое необходимо учитывать взаимосвязь процессов диффузии, теплопередачи и химических реакций. В общем случае должны быть использованы уравнения движения, энергии, диффузии и условия протекания химических реакций – уравнения химической кинетики.

В газовой смеси тепловой поток определяется как теплопроводностью, так и диффузионным потоком энтальпии

.                                (6.1)

Здесь второй член – перенос энергии вследствие диффузии;  – плот-ность газовой смеси в рассматриваемой точке; ,  – массовая концентрация и скорость диффузии отдельного компонента газовой смеси;  – теплосодержание (энтальпия) i-го компонента

                              ,                                    (6.2)

где  – количество тепла, которое выделяется или поглощается при образовании i-го компонента (теплота реакции).

Уравнения диффузии многокомпонентных смесей сложны для анализа. Поэтому такую смесь заменяют эффективной бинарной смесью, в этом случае уравнения диффузии значительно упрощаются. По молекулярно-кинетической теории газов, диффузионный поток  вещества  зависит  от концентрационной  диффузии, термодиф-

фузии и бародиффузии, т. е.

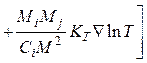  .                                     (6.3)

Здесь K_T = D_T /D_ij – термодиффузионное отношение; C_i, C_j – концентрации компонентов; M_i, M_j – молекулярные массы компонентов; D_ij, D_T – коэффициенты концентрационной и термической диффузии.

В приближении теории пограничного слоя  бародиффузия исключается. Влияние термодиффузии мало (~10 %). Поэтому определяющей является концентрационная диффузия и справедлив закон Фика

                              .                                     (6.4)

Выразим первый член в (6.1) через полное теплосодержание смеси газов в рассматриваемой точке

                              ,                                     (6.5)

откуда получим

                      .                           (6.6)

Подставляя (6.4) и (6.6) в (6.1), найдем

                      ,                       (6.7)

где  – критерий Льюиса, ,  .

Для газов в большинстве случаев критерий Льюиса близок  к единице () и выражение для потока тепла упрощается

.                                           (6.8)

В такой форме уравнение передачи тепла не зависит от механизма теплообмена и от скорости химических реакций. Дифференциальное  уравнение  энергии  пограничного  слоя  с  учетом (6.8) должно быть записано через полное теплосодержание газа:

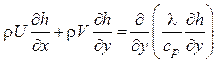                           .                            (6.9)

Уравнение диффузии i-го компонента газовой смеси с учетом (6.4) имеет вид

                   .                 (6.10)

Здесь  – скорость образования i-го компонента в результате химической реакции в рассматриваемой точке, т. е. при химических реакциях концентрации отдельных компонентов газа могут меняться. Наличие этого члена приводит к неподобию дифференциальных уравнений энергии (6.9) и диффузии (6.10).

Массовые же доли отдельных химических элементов во время реакций